Cantor 展开
Cantor展开 适用于对组合进行排列 和 数 得到双射函数
对于任意的集合 X,其中 Xi∈X, 且 i ∈(1, n), 其中的Xi都可以和另一个数一一对应,且
对于 X 有
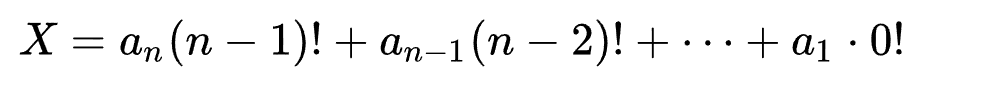
其中 an 为 对于第n为数其右侧小于该数的数量。
粗略推导:
eg {1, 5, 2, 3, 4}
对于第1位,小于其的数量为 0,所以 a[5] = 0
对于第2位,小于其的数量为4, 但是前面1会取掉一个, 所以a[2] = 4
对于第3位,小于其的数量为1, 但是前面1会取掉一个,所以a[3] = 3
对于第4位, 小于其的数量为2, 但是前面1 和 2 都会取掉一个, 所以 a[4] = 0
对于第5位, 小于其的数量为3, 但是前面1 2 3 都会取掉 , 所以a[5] = 0
综上,我们可以看到康托展开的思想是, 固定前i - 1位,求该位的小于其数量, 但因为前i - 1 位中可能会取掉这些数,这是我们想到一个方法, 因为 后i个数中小于该数的便是我们想要找的集合, 所以对于每一位,我们直接计算其后i位数。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号