LeetCode 287. 寻找重复数

我的LeetCode：https://leetcode-cn.com/u/ituring/

我的LeetCode刷题源码[GitHub]：https://github.com/izhoujie/Algorithmcii

LeetCode 287. 寻找重复数

题目

给定一个包含 n + 1 个整数的数组 nums，其数字都在 1 到 n 之间（包括 1 和 n），可知至少存在一个重复的整数。假设只有一个重复的整数，找出这个重复的数。

示例 1:

输入: [1,3,4,2,2]
输出: 2

示例 2:

输入: [3,1,3,4,2]
输出: 3

说明：

• 不能更改原数组（假设数组是只读的）。
• 只能使用额外的 $ {\color{Magenta}{\Omicron\left(1\right)}} $ 的空间。
• 时间复杂度小于 $ {\color{Magenta}{\Omicron\left(n^{2}\right)}} $) 。
• 数组中只有一个重复的数字，但它可能不止重复出现一次。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/find-the-duplicate-number
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解题思路

思路1-把数组看成有环的链表，寻找环的入口

如果把链表看做是有环的链表，那么环的入口就是重复的那个数；
根据题意，数组的值范围为[1, n]，而数组的长度为n+1，所以用任意数组的值作为下标都不存在越界的问题；
寻找环可以用快慢指针来进行，图解如下：


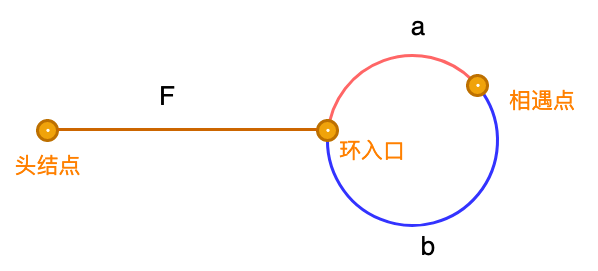
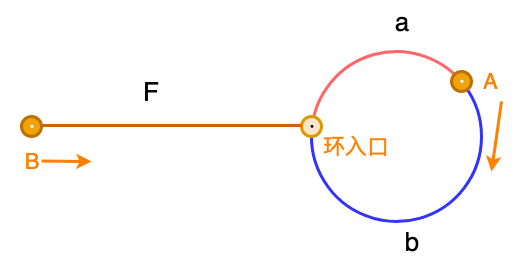
图中有几个关键信息：

• 快慢指针的起始位置:头节点；
• 快慢指针的相遇位置：相遇点；
• 环的入口即重复的数位置：环入口；

步骤：

1. 快慢指针，慢指针每次走1步，快指针每次走2步；
2. 两指针相遇后，将快指针重置为头结点，然后两指针同步每次均移动1步直至相遇，此时的节点即为环的入口（重复的数）；

解析：
快慢指针首次相遇的点必在环中（任意一点），假设快指针在环中转了n圈(很显然，n至少为1，不然无法相遇)再加a部分，根据运动长度，快指针是慢指针的两倍，则有：

\[2(F + a) = F + n(a + b) + a \]

即：

\[F = (n - 1) * (a + b) + b \]

忽略掉\((n - 1) * (a + b)\)的部分，重复的整个环不影响分析，那么就可以得到：

\[F = b \]

所以，在相遇后，重置其中一个指针为头结点，两个指针一个走F部分长度，一个走b部分长度，最终必会在环的入口节点相遇，也就找到了重复的数；

算法复杂度:

• 时间复杂度： $ {\color{Magenta}{\Omicron\left(n\right)}} $ 对数组进行了少量遍历
• 空间复杂度： $ {\color{Magenta}{\Omicron\left(1\right)}} $

算法源码示例

package leetcode;

/**
 * @author ZhouJie
 * @date 2020年5月31日 下午2:58:54 
 * @Description: 287. 寻找重复数
 *
 */
public class LeetCode_0287 {

}

class Solution_0287 {
	/**
	 * @author: ZhouJie
	 * @date: 2020年5月31日 下午2:59:24 
	 * @param: @param nums
	 * @param: @return
	 * @return: int
	 * @Description: 1-将数组看作有环链表，使用快慢指针寻找环入口；
	 *
	 */
	public int findDuplicate_1(int[] nums) {
		int fast = 0, slow = 0;
		while (true) {
			fast = nums[nums[fast]];
			slow = nums[slow];
			// 此时找到了环内的一个同步节点，然后重置其中一个指针为头节点，开始寻找环入口
			if (fast == slow) {
				fast = 0;
				while (nums[fast] != nums[slow]) {
					fast = nums[fast];
					slow = nums[slow];
				}
				return nums[fast];
			}
		}
	}
}