有序表

 

 

有序表只是一个接口，实现有很多，如：AVL,SB,RedBlackTree ,skipTable

AVL,SB,RedBlackTree是基于搜索二叉树设计出来的，增删改查是O(logn)

无重复节点，改成有重复节点可以这么设计：K,List<V>

二叉搜索树的增删改查：

查：val 大->root.right,val小->root.left,== return

增：查，查到空挂上

改：查到改值

删：分下面几种情况

前提是先查，查到后判段这个节点的情况

1、无左无右，直删

2、有左无右（让左该子去替它的环境）或有右无左，

 

 

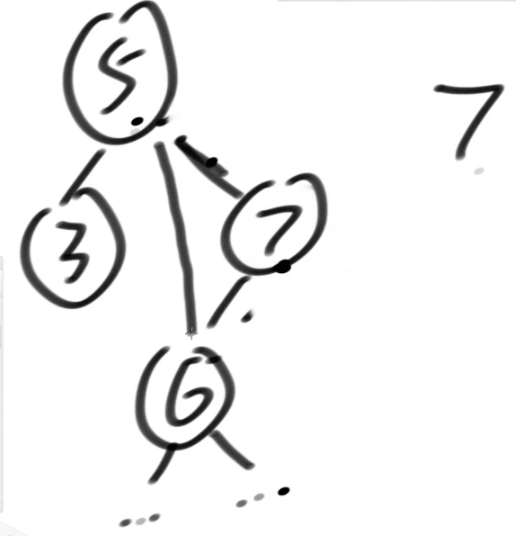
 3、有左有右

可以有两种方法：1:让左孩子的最右节点去替，2:让右孩子的最左节点去替

         

 

 

 

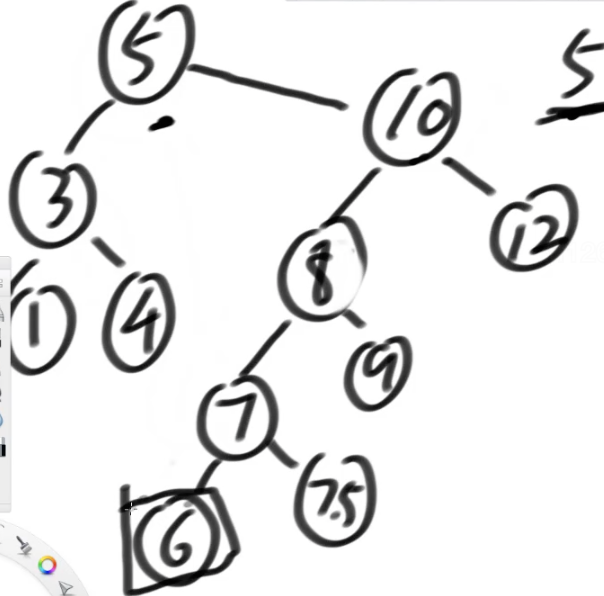
各个有序表的实现增删改查都一样，只是调整平衡不一样

  二叉搜索树的增删改：

public class AbstractBinarySearchTree {
    public static class Node{
        public Integer value;
        public Node parent;
        public Node left;
        public Node right;
        public Node(Integer value,Node parent,Node left,Node right){
            this.value=value;
            this.parent=parent;
            this.left=left;
            this.right=right;
        }
        public boolean isLeaf(){
            return left==null && right==null;
        }
    }

    Node root;
    int size;

    public Node search(int element){
        Node node=root;
        while(node!=null && node.value!=null && node.value!=element){
            if(element> node.value){
                node=node.right;
            }else {
                node=node.left;
            }
        }
        return node;
    }

    public void update(int element){
        Node node=search(element);
        if(node==null){
            return;
        }
        node.value=element;
    }

    protected Node createNode(int element,Node parent,Node left,Node right){
        return new Node(element,parent,left,right);
    }

    public Node insert(int element){
        if(root==null){
            root=createNode(element,null,null,null);
            size++;
            return root;
        }
        //search
        Node insertParentNode=null;
        Node searchTemNode=root;
        while(searchTemNode!=null && searchTemNode.value!=null){
            insertParentNode=searchTemNode;//最后一个不空的节点就是待加节点的父
            if(element> searchTemNode.value){
                searchTemNode=searchTemNode.right;
            }else{
                searchTemNode=searchTemNode.left;
            }
        }
        Node newNode=createNode(element,insertParentNode,null,null);
        if(insertParentNode.value>newNode.value){
            insertParentNode.left=newNode;
        }else{
            insertParentNode.right=newNode;
        }
        size++;
        return newNode;

    }
    public Node delete(int element){
        Node deleteNode=search(element);
        if(deleteNode==null){
            return null;
        }
        return delete(deleteNode);
    }

    protected Node delete(Node deleteNode){
        if(deleteNode==null){
            return null;
        }
        Node nodeToReturn=null;
        if(deleteNode.left==null){//综合了无左无右和有右无左的情况
            //transplant(a,b) b去替a的环境，a断联，把b返回
            nodeToReturn=transplant(deleteNode,deleteNode.right);
        }else if(deleteNode.right==null){//综合了无左无右和有左无右的情况
            nodeToReturn=transplant(deleteNode,deleteNode.left);
        }else{
            //找到右孩子的最左节点
            Node successorNode=getMinimun(deleteNode.right);
            if(successorNode.parent!=deleteNode){
                transplant(successorNode,successorNode.right);
                successorNode.right=deleteNode.right;
                successorNode.right.parent=successorNode;
            }
            transplant(deleteNode,successorNode);
            successorNode.left=deleteNode.left;
            successorNode.left.parent=successorNode;
            nodeToReturn=successorNode;

        }
        size--;
        return nodeToReturn;


    }
}

　　

扩展,可以改出很多API，TeeMap 中没有如下API，但可以通过SB树改

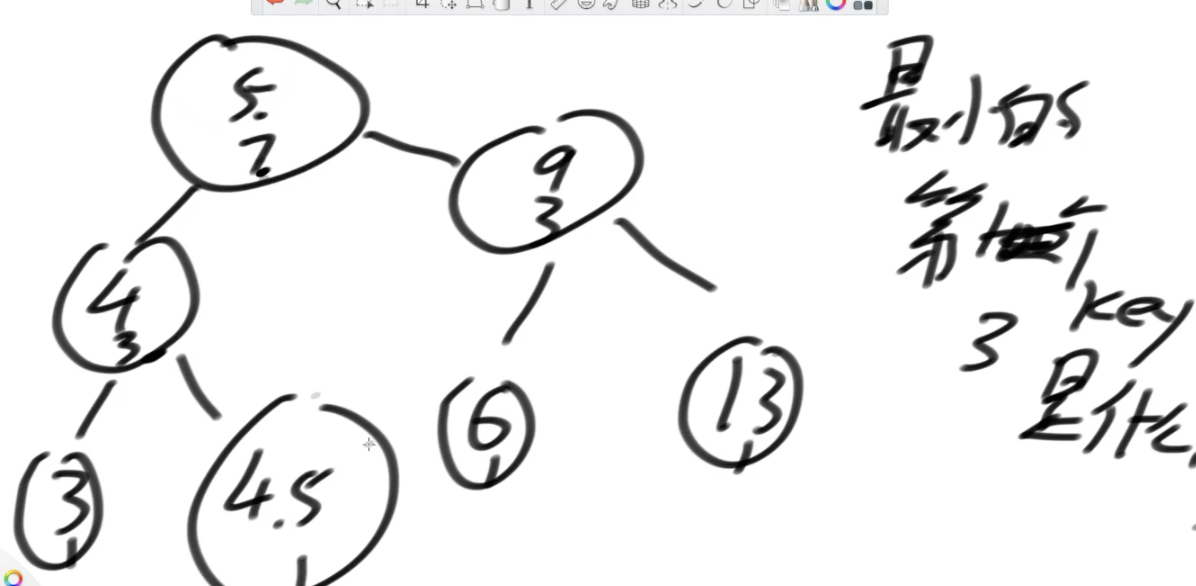
1:找到<=num离它最近的，>=num离它最近的，二分后大于往右，小于往左，

标记最后一个比它小的，和最后一个比它大的

 

2:找最小的第100个key是什么

 

 

 

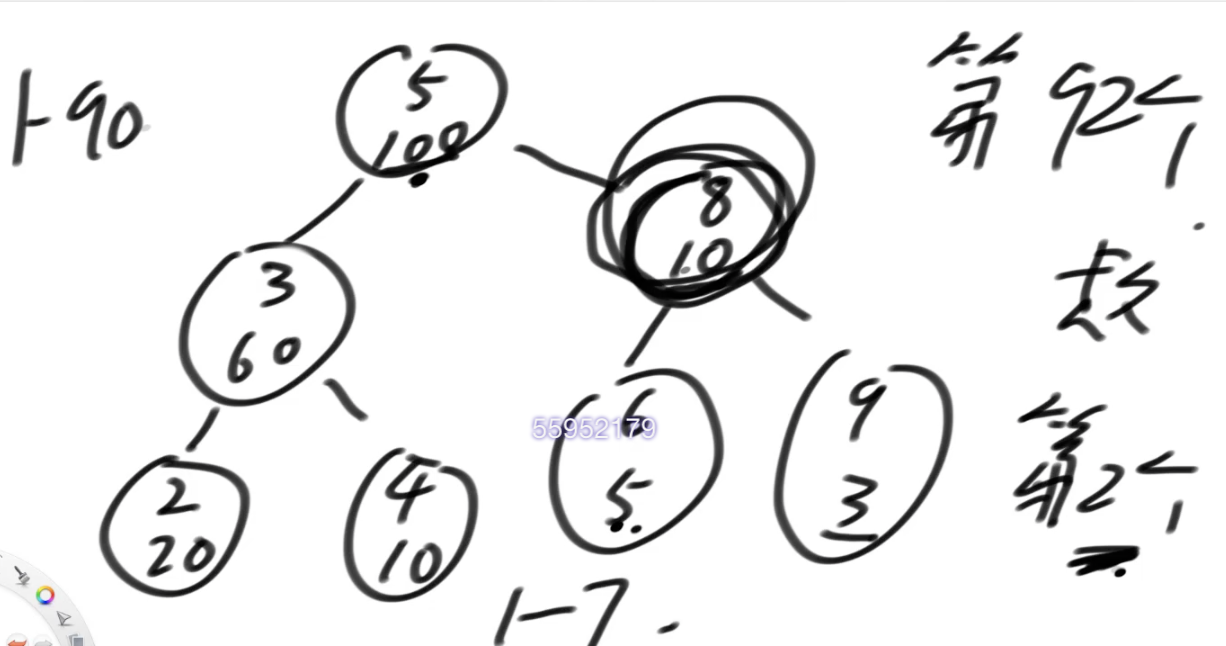
二叉搜索树通过增删改后，搜索的效率有可能会退化成O(n）

AVL,SB,RBT都是在维持平衡性

AVL树左右子树高度差不超过1

如何维持平衡性？左旋，右旋

 

 

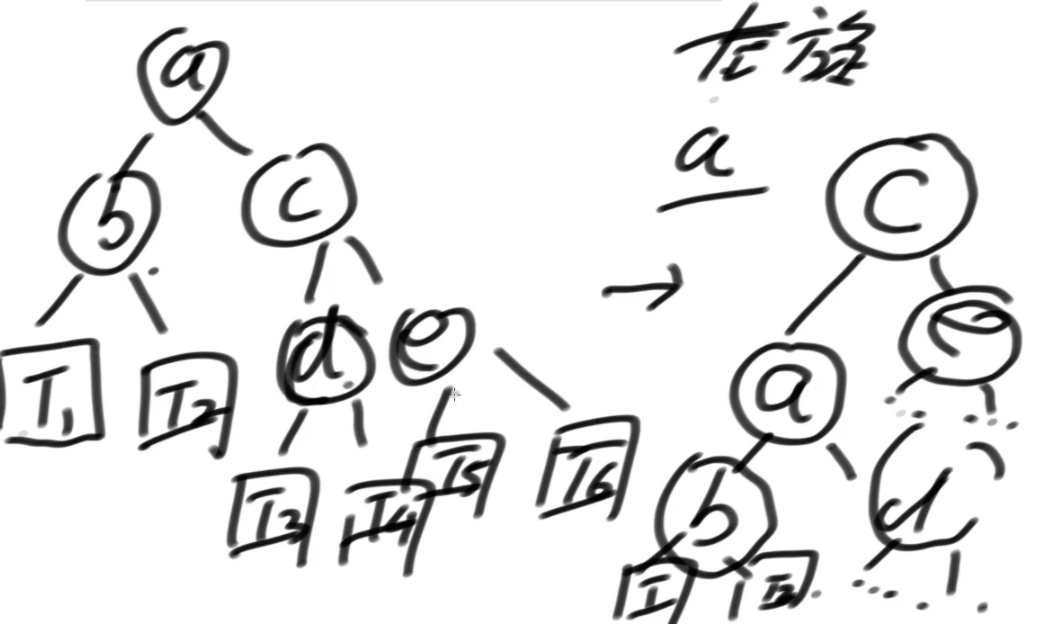
调整策略：4种违规

LL型：左边的左孩子过多->右旋

 

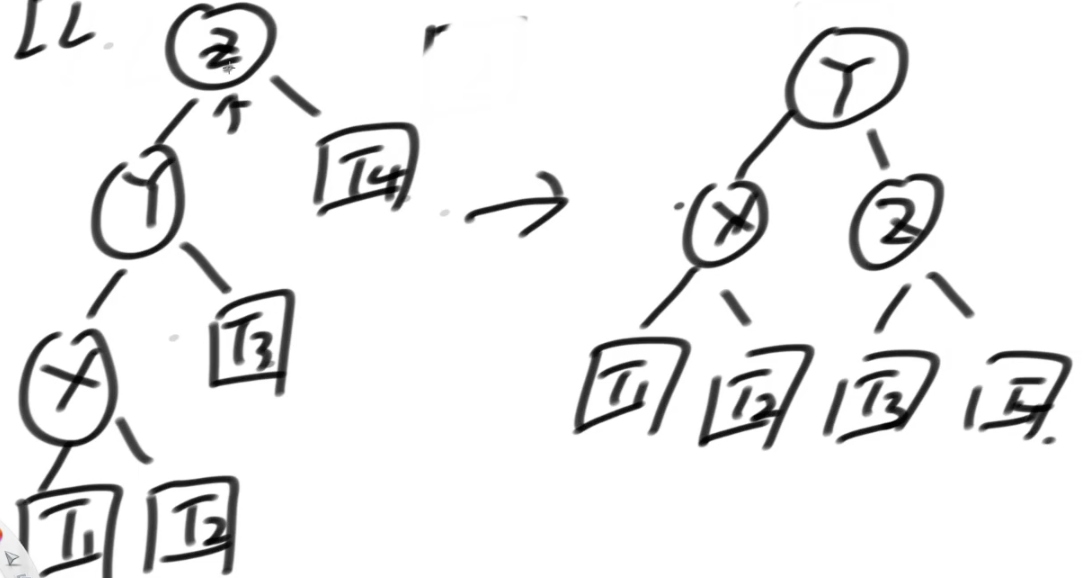
RR型：右边的右孩子过多->左旋

LR型：左边的右孩子过多->针对X想让它成于头，对Y先左旋，再整颗树右旋

 

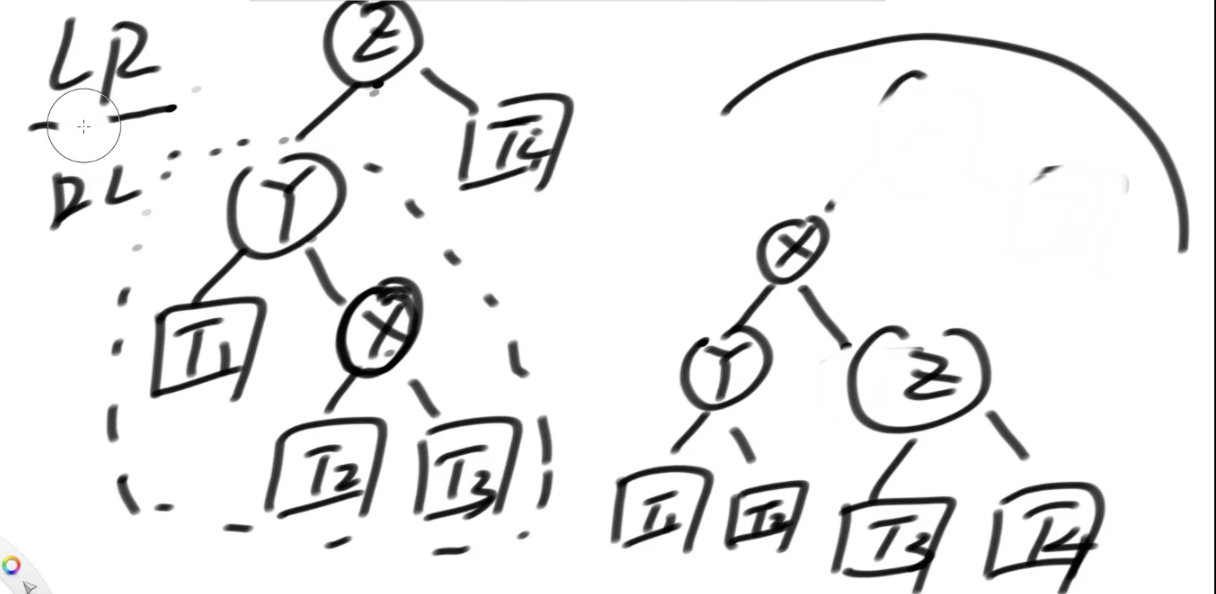
RL型：右边的左孩子过多->先右旋，再左旋

 private void avlRebalance(Node node,Node parent){
        int lH=node.left==null?-1:node.left.height;
        int rH=node.right==null?-1:node.right.height;
        int nodeBalance=rH-lH;
        if(nodeBalance==2){
            if(node.right.right!=null){
                node=avlRotaleft(node);
                break;
            }else{
                node=doubleRotateRightLeft(node);
                break;
            }
        }else if(nodeBalance==-2){
            if(node.left.left!=null){
                node=avlRotateRight(node);
                break;
            }else{
                node=doubleRotateLeftRight(node);
                break;
            }
        }else{
            updateHeight(node);
        }
    }

　　

SB树：API好改

AVL树维持了一个高度信息，高度差不能超过1，

而SB树是要求叔叔节点数不能小于任何侄子的节点数，如此规定后，左树子树的节点数不会超过2倍多

 调整策略和AVL树一样，4种违规

1、LL型：对X来说，是R违规了，a的节点数比R多

2、LR型：对X来说，是R违规了，b的节点数比R多

3、RR型：对X来说，是L违规了，d的节点数比R多

4、RL型：对X来说，是L违规了，c的节点数比R多

为什么这4种只有一种违规，因为插入和删除都是一个个插入和删除的，插删后都是从下往上查平衡，所以不会出现多种违规的情况

在这4种情况下如何调整？maintain

LL：X右旋，谁的子树发生了变化，还要miantain一下

 

 

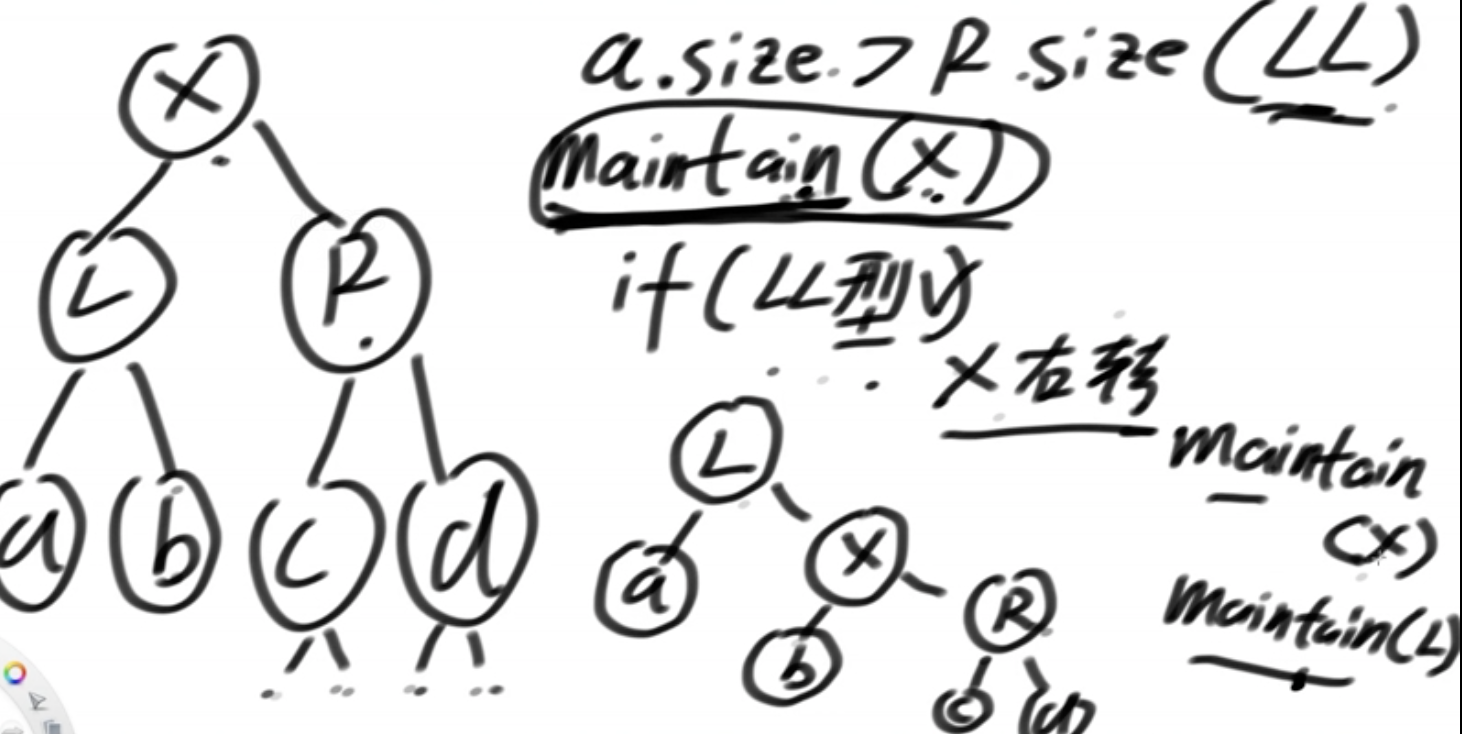
RR：X左旋，谁的子树发生了变化，还要miantain一下

LR：先对L左旋，再对X右旋，再m(L),m(x),m(b)

 

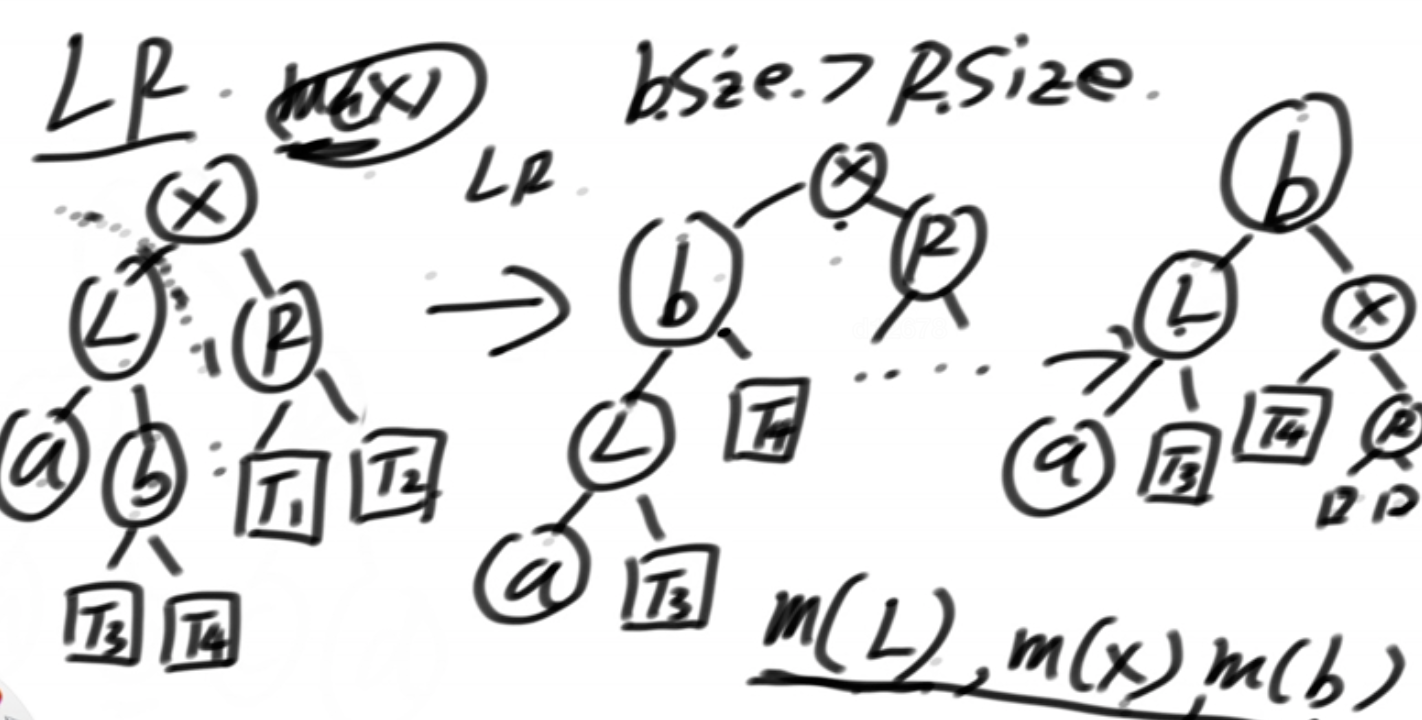
 RL:同理

SB左右旋后，还有递归行为，但时间复杂度进了是O(logn)

在删除节点时可以不调，在插入时统一调

平衡指标只能是size(不同的key的数量)，每个节点收了多少个节点用times,  size,times是两个不同的字段

不同的key, 一共的key