构造二叉树

106. 从中序与后序遍历序列构造二叉树

根据一棵树的中序遍历与后序遍历构造二叉树。

注意:
你可以假设树中没有重复的元素。

例如，给出

中序遍历 inorder = [9,3,15,20,7]
后序遍历 postorder = [9,15,7,20,3]
返回如下的二叉树：

3
/ \
9 20
/ \
15 7

 public TreeNode buildTree(int[] inorder, int[] postorder) {
            return build(inorder,0,inorder.length-1,postorder,0,postorder.length-1);
        }

        private TreeNode build(int[] inorder,int L1,int R1,int[] postorder,int L2,int R2){
            if(L1>R1){
                return null;
            }
            //only one element
            if(L1==R1){
                return new TreeNode(inorder[L1]);
            }

            TreeNode head=new TreeNode(postorder[R2]);
            //find index
            int index=0;
            for(int i=L1;i<=R1;i++){
                if(inorder[i]==postorder[R2]){
                    index=i;
                }
            }

            head.left=build(inorder,L1,index-1,postorder,L2,L2+index-L1-1);//0+0.  1-0
            head.right=build(inorder,index+1,R1,postorder,L2+index-L1,R2-1);
            return head;
        }

　　

105. 从前序与中序遍历序列构造二叉树

给定一棵树的前序遍历 preorder 与中序遍历  inorder。请构造二叉树并返回其根节点。

示例 1:

 

 

Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]

 public TreeNode buildTree(int[] preorder, int[] inorder) {
        if(preorder==null || inorder==null || preorder.length!=inorder.length){
            return null;
        }
        return build(inorder,0,inorder.length-1,preorder,0,preorder.length-1);

    }

    /**
    * preOrder[L1...R1]
    * inOrder[L2...R2]
    *preOrder[L1]-->rootVal. inOrder->index
    *
     */
     private TreeNode build(int[] inorder,int L1,int R1,int[] preorder,int L2,int R2){
         if(L1>R1){
             return null;
         }
         if(L1==R1){
             return new TreeNode(inorder[L1]);
         }
         int rootVal=preorder[L2];
         TreeNode head=new TreeNode(rootVal);
         int index=0;
         for(int i=L1;i<=R1;i++){
             if(rootVal==inorder[i]){
                 index=i;//1
             }
         }
        head.left=build(inorder,L1,index-1,preorder,L2+1,L2+index-L1);
        head.right=build(inorder,index+1,R1,preorder,L2+index-L1+1,R2);
        return head;

     }

　　

1008. 前序遍历构造二叉搜索树

返回与给定前序遍历 preorder 相匹配的二叉搜索树（binary search tree）的根结点。

(回想一下，二叉搜索树是二叉树的一种，其每个节点都满足以下规则，对于 node.left 的任何后代，值总 < node.val，而 node.right 的任何后代，值总 > node.val。此外，前序遍历首先显示节点 node 的值，然后遍历 node.left，接着遍历 node.right。）

题目保证，对于给定的测试用例，总能找到满足要求的二叉搜索树。

 

示例：

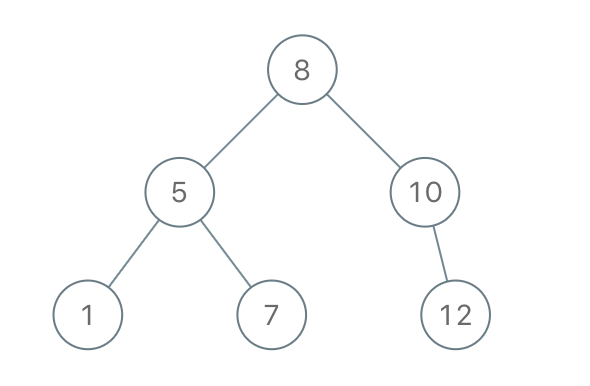
输入：[8,5,1,7,10,12]
输出：[8,5,10,1,7,null,12]

 

class Solution {
     public TreeNode bstFromPreorder(int[] preorder) {
        if(preorder==null){
            return null;
        }
        return build(preorder,0,preorder.length-1);

    }

    public TreeNode build(int[] preorder,int L,int R){

        if(L>R){
            return null;
        }
        if(L==R){
            return new TreeNode(preorder[L]);
        }
        int less=L;
        for(int i=L+1;i<=R;i++){
            if(preorder[i]<preorder[L]){
               less=i;
            }
        }
        TreeNode head=new TreeNode(preorder[L]);
        head.left=build(preorder,L+1,less);
        head.right=build(preorder,less+1,R);
        return head;
    }

}

　　

 

654. 最大二叉树

给定一个不含重复元素的整数数组 nums 。一个以此数组直接递归构建的 最大二叉树 定义如下：

二叉树的根是数组 nums 中的最大元素。
左子树是通过数组中 最大值左边部分 递归构造出的最大二叉树。
右子树是通过数组中 最大值右边部分 递归构造出的最大二叉树。
返回有给定数组 nums 构建的 最大二叉树 。

 

示例 1：

 

 

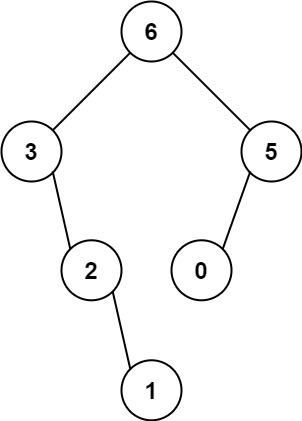
 public TreeNode constructMaximumBinaryTree(int[] nums) {
        //arr[L..R] findMax ->index head
        //arr[L..index-1] findMax head.left
        //arr[index+1..R] findMax head.right
        return build(nums,0,nums.length-1);
    }
    private TreeNode build(int[] nums,int L,int R){
        if(L>R){
            return null;
        }
        if(L==R){
            return new TreeNode(nums[L]);
        }
        int index=findMaxValueIndex(nums,L,R);
        TreeNode head=new TreeNode(nums[index]);
        head.left=build(nums,L,index-1);
        head.right=build(nums,index+1,R);
        return head;
    }
    private int findMaxValueIndex(int[] nums,int L,int R){
        int max=nums[L];
        int index=L;
        for(int i=L+1;i<=R;i++){
            if(max<nums[i]){
                max=nums[i];
                index=i;
            }
        }
        return index;

    }

　　

617. 合并二叉树

给定两个二叉树，想象当你将它们中的一个覆盖到另一个上时，两个二叉树的一些节点便会重叠。

你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠，那么将他们的值相加作为节点合并后的新值，否则不为 NULL 的节点将直接作为新二叉树的节点。

示例 1:

注意: 合并必须从两个树的根节点开始。

 public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        return merge(root1,root2);
    }

    private TreeNode merge(TreeNode root1,TreeNode root2){
        if(root1==null && root2==null){
            return null;
        }
        if(root1==null){
            return root2;
        }
        if(root2==null){
            return root1;
        }
        TreeNode head=new TreeNode(root1.val+root2.val);
        head.left=merge(root1.left,root2.left);
        head.right=merge(root1.right,root2.right);
        return head;
    }