46.全排列

给定一个 没有重复 数字的序列，返回其所有可能的全排列。

示例: 输入: [1,2,3] 输出: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ]

思路

排列问题:

以[1,2,3]为例，抽象成树形结构如下：

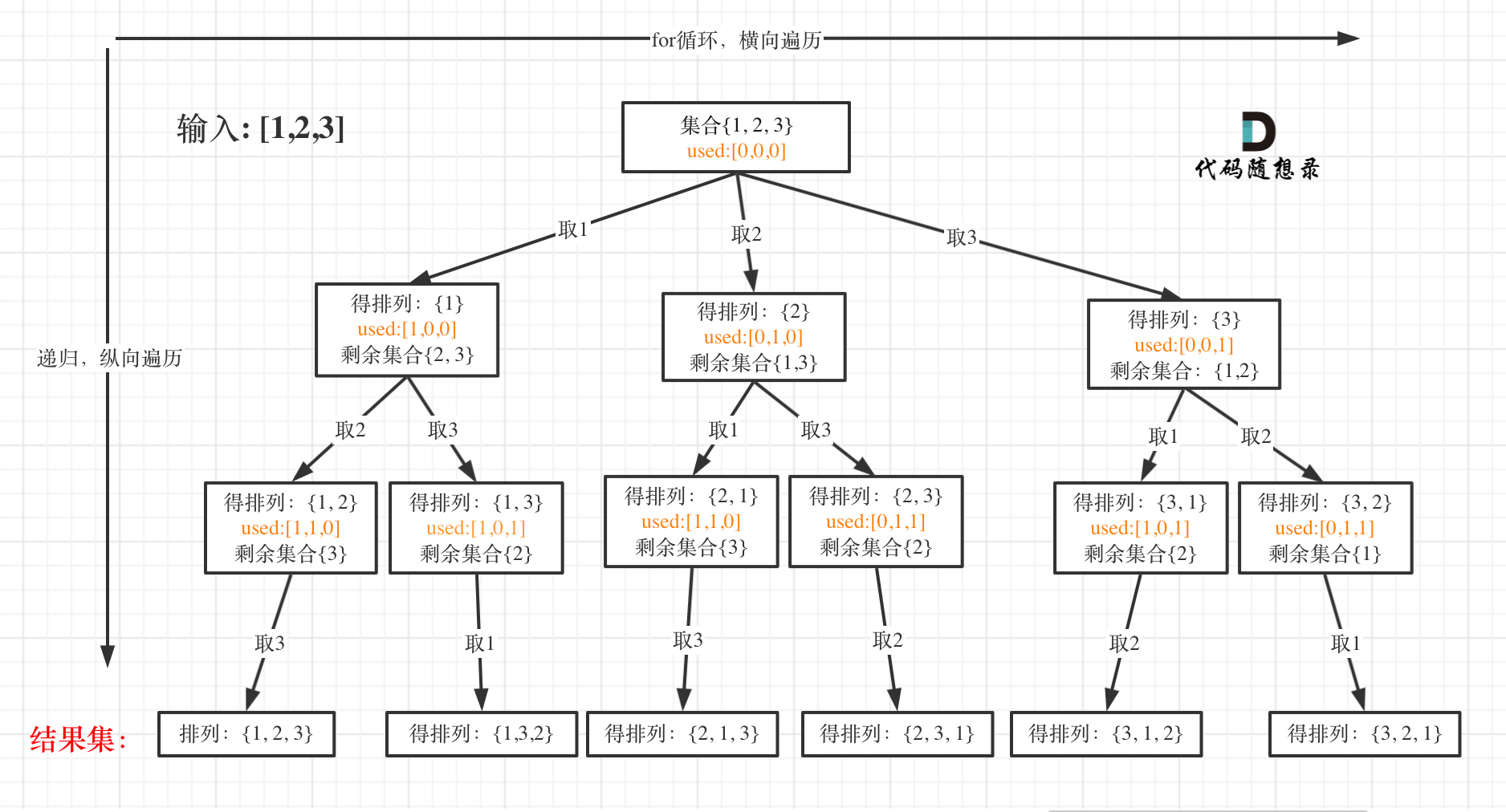
回溯三部曲

• 递归函数参数

首先排列是有序的，也就是说[1,2] 和[2,1] 是两个集合，这和之前分析的子集以及组合所不同的地方。

可以看出元素1在[1,2]中已经使用过了，但是在[2,1]中还要在使用一次1，所以处理排列问题就不用使用startIndex了。

但排列问题需要一个used数组，标记已经选择的元素，如图橘黄色部分所示

 

• 递归终止条件

可以看出叶子节点，就是收割结果的地方。

那么什么时候，算是到达叶子节点呢？

当收集元素的数组path的大小达到和nums数组一样大的时候，说明找到了一个全排列，也表示到达了叶子节点。

 

• 单层搜索的逻辑

这里和77.组合问题 (opens new window)、131.切割问题 (opens new window)和78.子集问题 (opens new window)最大的不同就是for循环里不用startIndex了。

因为排列问题，每次都要从头开始搜索，例如元素1在[1,2]中已经使用过了，但是在[2,1]中还要再使用一次1。

而used数组，其实就是记录此时path里都有哪些元素使用了，一个排列里一个元素只能使用一次。

 

class Solution {
    List<List<Integer>> res=new ArrayList<>();
    List<Integer> path=new ArrayList<>();
    boolean[] used;
    public List<List<Integer>> permute(int[] nums) {

      used=new boolean[nums.length];
      process(nums);
      return res;

    }

    private void process(int[] nums){
      if(path.size()==nums.length){
          res.add(new ArrayList<>(path));
      }

      for(int i=0;i<nums.length;i++){
          if(used[i]){
              continue;
          }
          used[i]=true;
          path.add(nums[i]);
          process(nums);
          path.remove(path.size()-1);
          used[i]=false;
      }

    }
}

　　

大家此时可以感受出排列问题的不同：

• 每层都是从0开始搜索而不是startIndex
• 需要used数组记录path里都放了哪些元素了

 

下面是另一种解法

class Solution {
    public List<List<Integer>> permute(int[] nums) {

        List<List<Integer>> ans=new ArrayList<>();
        List<Integer> numList=new ArrayList<>();
        for(int i=0;i<nums.length;i++){
            numList.add(nums[i]);
        }
        List<Integer> path=new ArrayList<>();
        
        process(numList,path,ans,numList.size());
        return ans;

    }

    private void process(List<Integer> numList,List<Integer> path,List<List<Integer>> ans,int size){
        //base case
       if(numList.isEmpty()){
           ans.add(path);
           return;
       }
    
       for(int i=0;i<numList.size();i++){
           //这里注意不能直接 path.add(numList.get(i))，否则递归后会把所有数字都会收集到path中
           //而是要用新的变量来接
           List<Integer> pick=new ArrayList<>(path);
           pick.add(numList.get(i));
           List<Integer> nextList=new ArrayList<>(numList);
           nextList.remove(i);
           process(nextList,pick,ans,numList.size());
       }
    }
}