236. 二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例 1:
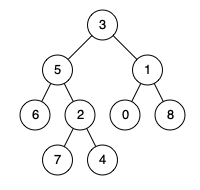
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出:3
解释:节点 5 和节点 1 的最近公共祖先是节点 3 。
示例 2:
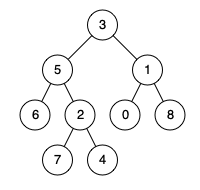
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出:5
解释:节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root==null){
return root;
}
if(root==p || root==q){
return root;
}
TreeNode left = lowestCommonAncestor(root.left,p,q);
TreeNode right = lowestCommonAncestor(root.right,p,q);
if(left!=null && right!=null){
return root;
}
if(left!=null){
return left;
}
if(right!=null){
return right;
}
return null;
}
1644. 二叉树的最近公共祖先 II
给定一棵二叉树的根节点 root,返回给定节点 p 和 q 的最近公共祖先(LCA)节点。如果 p 或 q 之一不存在于该二叉树中,返回 null。树中的每个节点值都是互不相同的。
根据维基百科中对最近公共祖先节点的定义:“两个节点 p 和 q 在二叉树 T 中的最近公共祖先节点是后代节点中既包括 p 又包括 q 的最深节点(我们允许一个节点为自身的一个后代节点)”。一个节点 x 的后代节点是节点 x 到某一叶节点间的路径中的节点 y。
示例 1:
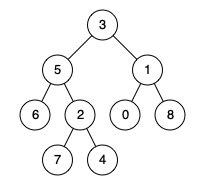
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和 1 的共同祖先节点是 3。
示例 2:
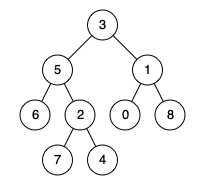
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和 4 的共同祖先节点是 5。根据共同祖先节点的定义,一个节点可以是自身的后代节点。
示例 3:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 10
输出: null
解释: 节点 10 不存在于树中,所以返回 null。
/**
* 找最低公共租先
**/
public static TreeNode lowestCommon(TreeNode head, TreeNode o1, TreeNode o2){
Info info=process(head,o1,o2);
return info.findAns;
}
/**
* 返回O1和O2的最低公共祖先
* 分析可能性:以X为头的节点
* 1:即无O1,也无O2,X整树不存在低共
* 2:O1和O2只有一个,低共不存在,记录(O1,O2)状态
* 3:O1,O2,都在,全左树(左树的低共就是整树的低共),全右树,左右子树=》X
*
* 信息整理:
* 是否发现O1和O2的公共祖先
* 整树是否发现了O1,是否发现了O2
*/
public static Info process(TreeNode x, TreeNode o1, TreeNode o2){
if(x==null){
return new Info(false,false,null);
}
Info leftInfo=process(x.left,o1,o2);
Info rightInfo=process(x.right,o1,o2);
if(leftInfo.findAns!=null){
return new Info(true,true,leftInfo.findAns);
}
if(rightInfo.findAns!=null){
return new Info(true,true,rightInfo.findAns);
}
//左右树都没有发现最低公共组先
if(leftInfo.findO1 && rightInfo.findO2){
return new Info(true,true,x);
}
if(leftInfo.findO2 && rightInfo.findO1){
return new Info(true,true,x);
}
//左右两树都没有发现最低公共,而且不交汇
//左右两树只包o1,或只包O2,或者什么都没有发现
boolean findO1=x==o1;
boolean findO2=x==o2;
if(leftInfo.findO1||rightInfo.findO1){
if(findO2){
return new Info(true,true,x);
}else{
return new Info(true,false,null);
}
}
if(leftInfo.findO2||rightInfo.findO2){
if(findO1){
return new Info(true,true,x);
}else{
return new Info(false,true,null);
}
}
//左右两树都没有发现
return new Info(findO1,findO2,null);//注意这里,是new Info(findO1,findO2,null)不是new Info(false,false,null)
}
public static class Info{
public boolean findO1;
public boolean findO2;
public TreeNode findAns;
public Info(boolean f1, boolean f2, TreeNode ans)
{
this.findO1=f1;
this.findO2=f2;
this.findAns=ans;
}
}
剑指 Offer 68 - I. 二叉搜索树的最近公共祖先
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
示例 1:
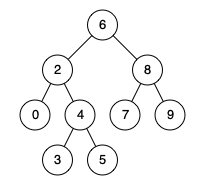
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
说明:
- 所有节点的值都是唯一的。
- p、q 为不同节点且均存在于给定的二叉搜索树中。
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root==null){
return root;
}
if(root==p || root==q){
return root;
}
TreeNode left=lowestCommonAncestor(root.left,p,q);
TreeNode right=lowestCommonAncestor(root.right,p,q);
if(left!=null && right!=null){
return root;
}
if(left!=null){
return left;
}
if(right!=null){
return right;
}
return null;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号