5. 最长回文子串（Manachert算法）
Manachert算法：
求一个字符串串最长的回文子串
122131221
暴力法：每个字符都当作是中心字符，向两边扩，找到所有的
a121bcb121ckf
113
但是这外求法有一个问题如果回文是even是找不到的
122131221
1221就找不到了，因为没法找到虚轴
所以要做以下处理
#1#2#2#1#3
# 1 # 2 # 2 # 1 # 3 # 1 # 2 # 2 # 1 #
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
1 3 1 3 9 ........19
19/2=9
9/2=4
虚轴只是一个辅助作用，所以加什么特殊字符都可以，不会影响实轴
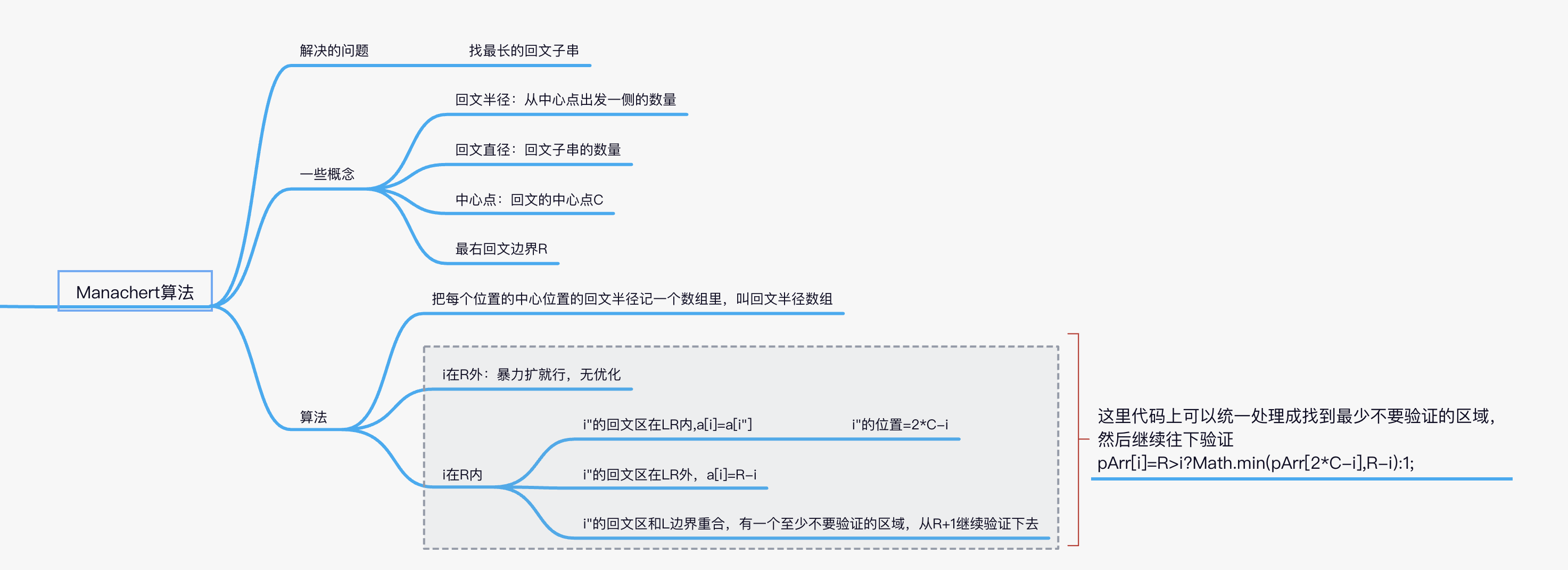
一些概念：
1：回文半径：从中心点从出发一侧的数量，直径：所有回文的数量
# 1 # 2 # 2 # 1 #
0 1 2 3 4 5 6 7 8
c
中心点c ：回文半径是5,直径是9
2:最右回文边界R，初始值-1
# 1 # 2 # 2 # 1 #
c 0 1 2 3 4 5 6 7 8
r 1 3 4
3:中心点在哪？
当R更新到8时，是哪个中心点使它更新到8的？
只要R更新，C一定更新
通过以上的概念
把每个位置的中心位置的回文半径记一个数组里，叫回文半径
R=-1；
i=0,arr[0]=1;R=1
i=0,arr[1]=2;
i=0,arr[2]=2;
i=0,arr[3]=4;
i=0,arr[4]=8;
用这个来加速过程
R：最右回文右边界
arr[i]=? 以i为中心能扩多大
1：i在R外：暴力扩就行，无优化
2：i在R内：
L a【 i" 】b C k【 i 】f R
A B
a[i"]=R"
情况1:如果i"的回文区在LR内,a[i]=a[i"]
证明：
a!=b----->k!=f
a==k
b==f
情况2：i"的回文区在LR外，a[i]=R-i
证明：
（ a【L i" ]b ） C k【 i R】f
a==b
b==k
a!=f
----->k!=f
情况3：i"的回文区和L边界重合，有一个至少不要验证的区域，从R+1继续验证下去
public static int maxLcpsLength(String str){
if(str==null||str.length()==0){
return 0;
}
char[] charArr=manacherString(str);
int[] pArr=new int[charArr.length];
int C=-1;//中心点位置
//[L C R-1]R
int R=-1;//R代表最右扩成功位置的下一个
int max=Integer.MIN_VALUE;
for(int i=0;i!=charArr.length;i++){
//i位置扩出来的答案，i位置扩的区域，至少是多大
//R>i，表示i在R内，2*C-i就是i"的位置，则i的回文半径最少是i"的回文半径和R-i较少的那一个
//i在R外，i的回文半径最少是1
//表示i最少的回文半径，这个区域是不用验的，接着这个位置继续扩
pArr[i]=R>i?Math.min(pArr[2*C-i],R-i):1;
//while内的条件代表，这个半径没有越界
while(i+pArr[i]<charArr.length&& i-pArr[i]>-1){
//（ a【L i" ]b ） C k【 i R】f
if(charArr[i+pArr[i]]==charArr[i-pArr[i]]){
//相等，则扩
pArr[i]++;
}else{
break;
}
}
//看有没有刷新R
if(i+pArr[i]>R){
//R更新
R=i+pArr[i];
//中心点也更新
C=i;
}
//求最大值
max=Math.max(max,pArr[i]);
}
return max-1;// 最大回文串2max/2-1，示例回文半径是5的情况
}
5. 最长回文子串
给你一个字符串 s，找到 s 中最长的回文子串。
示例 1：
输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。
示例 2：
输入：s = "cbbd"
输出："bb"
示例 3：
输入：s = "a"
输出："a"
示例 4：
输入：s = "ac"
输出："a"
class Solution {
public String longestPalindrome(String s) {
if(s.length()==1){
return s;
}
String str=getManacherStr(s);
char[] chs=str.toCharArray();
int[] pArr=new int[chs.length];
int C=-1;
int R=-1;
int j=-1;
int max=Integer.MIN_VALUE;
for(int i=0;i<chs.length;i++){
pArr[i]=R>i?Math.min(pArr[2*C-i],R-i):1;
while(i+pArr[i]<chs.length&& i-pArr[i]> -1){
if(chs[i+pArr[i]]==chs[i-pArr[i]]){
pArr[i]++;
}else{
break;
}
}
if(i+pArr[i]>R){//推动R
R=i+pArr[i];
C=i;//推动R的中心点位置
}
//收集最大回文的结果
if(pArr[i]>max){
max=pArr[i];//最大回文半径
j=i;//最大回文半径时的中心点
}
}
//j,max
String bigStr=str.substring(j-max+1,j+max);
if(bigStr==""){
return s.substring(0,1);
}else{
return removeManacherStr(bigStr);
}
}
public String removeManacherStr(String str){
String res="";
if(str.length()==1){
if(str.equals("#")){
return res;
}else{
return str;
}
}
for(int i=0;i<str.length();i++){
if(str.charAt(i)!='#'){
res+=str.charAt(i);
}
}
return res;
}
public String getManacherStr(String str){
String res="#";
for(int i=0;i<str.length();i++){
res+=str.charAt(i)+"#";
}
return res;
}
}
