Tensorflow练习实现线性回归

Tensorflow练习实现线性回归

import matplotlib.pyplot as plt
import numpy as np
import tensorflow.compat.v1 as tf
import pandas as pd
rng = np.random
# 处理tensorflow2.0不向下兼容的问题
tf.compat.v1.disable_eager_execution()
# 学习率
learning_rate = 0.01
# 迭代次数1000
training_epochs = 1000
# 每隔50次显示训练结果
display_step = 50
# 训练数据读入
data = pd.read_table('./data/practise/ex1data1.txt',
                     header=None,
                     delimiter=',')
train_X = np.asarray(data.iloc[:, 0])
train_Y = np.asarray(data.iloc[:, 1])
# darray.shape返回数组的形状（a*b）a为数组的列，b为数据的行
n_samples = train_X.shape[0]

# plt.scatter(train_X,train_Y)
# plt.show()
#占位符 见54行X的赋值
X = tf.placeholder('float')
Y = tf.placeholder('float')
#创建模型参数作为变量
W = tf.Variable(rng.randn(), name="weight")
b = tf.Variable(rng.randn(), name="bias")
#决策函数
pred = tf.add(tf.multiply(X, W), b)
# 代价函数   Σ(wx+b-Y)^2/2n 均方差
cost = tf.reduce_sum(tf.pow(pred - Y, 2)) / (2 * n_samples)
'''
    优化函数 GradientDescentOptimizer->梯度下降优化算法
    learning_rate:学习率
    minimize() 函数处理了梯度计算和参数更新两个操作
    optimizer.minimize(loss, var_list)
    compute_gradients 计算梯度
    apply_gradients 使用计算得到的梯度来更新对应的variable
'''
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost)
# 模型参数初始化
init = tf.initialize_all_variables()

with tf.Session() as sess:
    sess.run(init)

    # 迭代训练数据0
    for epoch in range(training_epochs):
        for (x, y) in zip(train_X, train_Y):
            # feed_dict 即赋值，迭代数据，X为占位符，x为实际值
            sess.run(optimizer, feed_dict={X: x, Y: y})
            # 每隔display_step次显示一次损失函数的值
        if (epoch + 1) % display_step == 0:
            c = sess.run(cost, feed_dict={X: train_X, Y: train_Y})
            print("Epoch: ", '%04d' % (epoch + 1), "cost=", "{:.9f}".format(c),
                  "w= ", sess.run(W),"b= ",sess.run(b))
    print("Optimization Finished!")
    # 计算最终损失函数值
    training_cost = sess.run(cost, feed_dict={X: train_X, Y: train_Y})
    print("Training cost= ", training_cost, "w= ", sess.run(W), "b= ",
          sess.run(b), '\n')

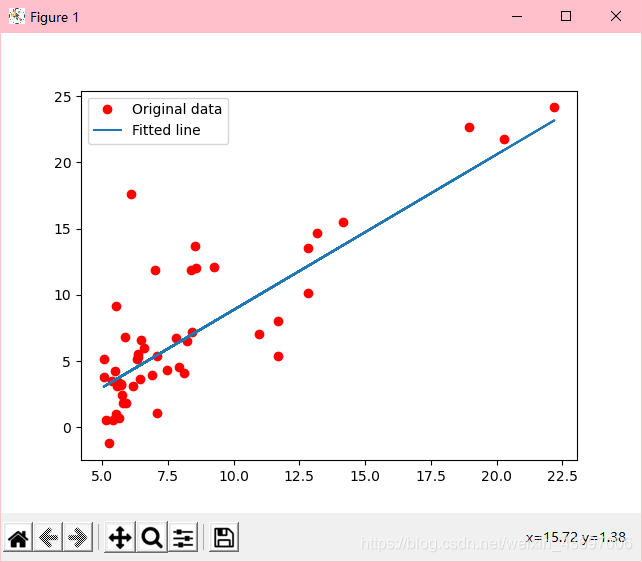
    plt.plot(train_X, train_Y, 'ro', label='Original data')
    # 拟合曲线
    plt.plot(train_X, sess.run(W) * train_X + sess.run(b), label='Fitted line')
    plt.legend()
    plt.show()
    
    data = pd.read_table('./data/practise/ex1data2.txt',
                     header=None,
                     delimiter=',')
    test_x = np.asarray(data.iloc[:, 0])
    test_y = np.asarray(data.iloc[:, 1])
    # 测试数据
    print("Testing... ")
    testing_cost=sess.run(tf.reduce_sum(tf.pow(pred-Y,Y))/(2*test_x.shape[0]),feed_dict={X:test_x,Y:test_y})
    print("Testing cost= ",testing_cost)
    
    print("absolute mean square loss difference: ",abs(training_cost-testing_cost))
    
    plt.plot(test_x,test_y,'bo',label="testing data")
    # 测试拟合曲线
    plt.plot(train_X,sess.run(W)*train_X+sess.run(b),label="Fitted line")
    plt.legend()
    plt.show()