【转】康拓展开

———本文转自：http://www.cnblogs.com/1-2-3/archive/2011/04/25/generate-permutation-part2.html

1、康托展开
　　康托展开的公式是 X=an*(n-1)!+an-1*(n-2)!+...+ai*(i-1)!+...+a2*1!+a1*0! 其中，ai为当前未出现的元素中是排在第几个（从0开始）。
　　这个公式可能看着让人头大，最好举个例子来说明一下。例如，有一个数组 s = ["A", "B", "C", "D"]，它的一个排列 s1 = ["D", "B", "A", "C"]，现在要把 s1 映射成 X。n 指的是数组的长度，也就是4，所以
X(s1) = a4*3! + a3*2! + a2*1! + a1*0!
关键问题是 a4、a3、a2 和 a1 等于啥？
a4 = "D" 这个元素在子数组 ["D", "B", "A", "C"] 中是第几大的元素。"A"是第0大的元素，"B"是第1大的元素，"C" 是第2大的元素，"D"是第3大的元素，所以 a4 = 3。
a3 = "B" 这个元素在子数组 ["B", "A", "C"] 中是第几大的元素。"A"是第0大的元素，"B"是第1大的元素，"C" 是第2大的元素，所以 a3 = 1。
a2 = "A" 这个元素在子数组 ["A", "C"] 中是第几大的元素。"A"是第0大的元素，"C"是第1大的元素，所以 a2 = 0。
a1 = "C" 这个元素在子数组 ["C"] 中是第几大的元素。"C" 是第0大的元素，所以 a1 = 0。（因为子数组只有1个元素，所以a1总是为0）
所以，X(s1) = 3*3! + 1*2! + 0*1! + 0*0! = 20。

2、通过康托逆展开生成全排列
　　如果已知 s = ["A", "B", "C", "D"]，X(s1) = 20，能否推出 s1 = ["D", "B", "A", "C"] 呢？
　　因为已知 X(s1) = a4*3! + a3*2! + a2*1! + a1*0! = 20，所以问题变成由 20 能否唯一地映射出一组 a4、a3、a2、a1？如果不考虑 ai 的取值范围，有
3*3! + 1*2! + 0*1! + 0*0! = 20
2*3! + 4*2! + 0*1! + 0*0! = 20
1*3! + 7*2! + 0*1! + 0*0! = 20
0*3! + 10*2! + 0*1! + 0*0! = 20
0*3! + 0*2! + 20*1! + 0*0! = 20
等等。但是满足 0 <= ai <= n-1 的只有第一组。可以使用辗转相除的方法得到 ai，如下图所示：

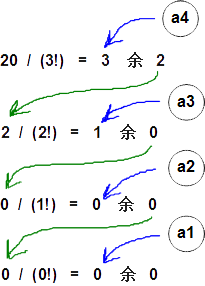
知道了a4、a3、a2、a1的值，就可以知道s1[0] 是子数组["A", "B", "C", "D"]中第3大的元素 "D"，s1[1] 是子数组 ["A", "B", "C"] 中第1大的元素"B"，s1[2] 是子数组 ["A", "C"] 中第0大的元素"A"，s[3] 是子数组 ["C"] 中第0大的元素"C"，所以s1 = ["D", "B", "A", "C"]。
这样我们就能写出一个函数，它可以返回  s 的第 m 个排列。

 

以下是代码(以不超过10位的字符串为例)，有所修改：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
using namespace std;
const int maxn = 10;
char s[maxn+1];
//计算x的阶乘
int Cal(int x)
{
    int ans = 1;
    for (int i = 1; i <= x; i++) ans *= i;
    return ans;
}
//得到字符在字符串其后字符中为第几大
int ID(char* c, char*s,int len)
{
    int re = 0;
    for (char*t = c + 1; t < s + len; t++)
    {
        if (*c >= *t)re++;
    }
    return re;
}
//得到字符串康拓展开值（从0开始）
int V_CantorExpansion(char *s)
{
    int ret = 0;
    int len = strlen(s);
    for (int i = 0; i < len; i++)
    {
        ret += ID(s+i,s,len)*Cal(len - i - 1);
    }
    return ret;
}
//求k个字符（升序）第n个全排列
string Inv_CantorExpansion(char*s, int n)
{
    int len = strlen(s);
    string ini = s;
    string ret;
    for (int i = len - 1; i>= 0; --i)
    {
        int pos = n / Cal(i);
        ret.push_back(ini[pos]);
        ini.erase(pos, 1);
        n %= Cal(i);
    }
    return ret;
}
int main()
{

    while (1)
    {
        printf("输入不超过10位的字符串计算康拓展开值:\n");
        scanf("%s", s);
        printf("%d\n", V_CantorExpansion(s));
        printf("输入不超过10位的初始字符串(升序)计算第n个全排列:\n");
        scanf("%s", s);
        int n;
        scanf("%d", &n);
        printf("%s\n", Inv_CantorExpansion(s, n).c_str());
    }
    return 0;
}