树上问题

树上问题涉及许多经典的算法技巧, 这里我们一个个枚举 "倍增 距离 重心 直径 差分"

倍增  

代表算法: LCA (最近公共祖先) 

LCA 介绍:

给你一颗树S, 对于任意给定两个节点from, to, 找到一个离根最远的节点x, 使得x是from, to的祖先, 同理寻找到的 x 也是from, to的最近公共祖先 那么我们用公式描述就是LCA(from, to) = x

看图: 

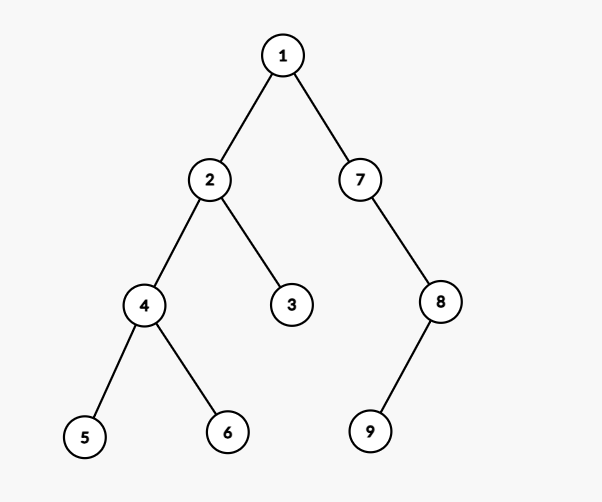
 如图对于节点3 4 我们明显发现离它最近的祖先是2及 LCA(3, 2) = 2 但是我们可以发现如果节点1 7那他的公共祖先是什么, 可以发现这两个点在同一颗子树上, 可以得到LCA(1, 7) = 7 我们清楚了LCA的直观描述, 那我们尝试使用代码解决这个问题, 这里将采用倍增的写法, 利用朴素进阶过渡.

朴素:

写法1:

对于两个节点from, to, 我们每次找到深度最大的点, 让它往上跳, 这两个点最后一定会相遇, 相遇的位置x 就是我们需要求出的最近公共祖先x  

写法2:(通常解放)

对于两个节点from, to, 我们深度最大的点向上跳, 使得两个点的深度相同, 后面一起往上跳, 最后相遇的位置x 就是我们需要求出的最近公共祖先x

结论:

不难得出对于朴素算法, 我们需要dfs预处理整棵树, 对于单次查询的复杂度是(n),如果对于多次查询O(q * n) 可能会导致时间超时

Code:

constexpr int N = 5e5 + 5;
int dep[N], dp[N];
vector <int> adj[N];

void dfs (int from, int fa) {
    dep[from] = dep[fa] + 1;
    dp[from] = fa;
    for (int to : adj[from]) {
        if (to == fa) continue;
        dfs (to, from);
    }
}

int lca (int x, int y) {
    if (dep[x] < dep[y]) swap(x, y);
    while (dep[y] < dep[x]) {
        x = dp[x];
    } 
    if (x == y) return y;
    while (x != y) {
        x = dp[x]; y = dp[y];
    } 
    if (!x) return 1;// 默认1是根节点
    return x;
}

倍增优化:

保证dep[from] > dp[to], 那么dep[from] - dp[to]的长度我们可以通过倍增来优化, 避免了暴力 调整后的深度相同后，找到LCA， 当两个节点的深度相同后，我们可以开始同时上跳这两个节点，直到它们的父节点相同，最终找到它们的LCA

解释: 任意整数都可以拆分为若干以2为底的幂项和 

Code:

constexpr int N = 5e4 + 5, M = 22;
int n, m, self, cnt = 0, ans = 0, dep[N], dp[N][M], head[N], diff[N], dist[N]; 

struct Edge {
    int to, w, nxt;
} edges[N << 1];
 
void init () {
    cnt = 0;
    for (int i = 1; i <= n; i++) {
        head[i] = 0, dep[i] = 0, dist[i] = 0; // diff[i] = 0; 
        for (int j = 0; j < M; j++) {
            dp[i][j] = 0;            
        }
    }
}

void add_edge (int from, int to, int w = 1) {
    edges[++cnt] = {to, w, head[from]};
    head[from] = cnt;
}

void dfs (int from, int fa) {
    dp[from][0] = fa, dep[from] = dep[fa] + 1;
    for (int i = 1; (1 << i) <= dep[from]; i++) {
        dp[from][i] = dp[dp[from][i - 1]][i - 1];
    } 
    for (int i = head[from]; i; i = edges[i].nxt) {
        if (edges[i].to == fa) continue; 
        dist[edges[i].to] = dist[from] + edges[i].w;
        dfs (edges[i].to, from);
    } 
} 

int lca (int from, int to) {
    if (dep[from] < dep[to]) swap(from, to); 
    for (int i = 20; i >= 0; i--) {
        if (dep[from] - (1 << i) >= dep[to]) from = dp[from][i];  
    }
    if (from == to) return to;
    for (int i = 20; i >= 0; i--) {
        if (dp[from][i] ^ dp[to][i]) {
            from = dp[from][i], to = dp[to][i];
        }
    }
    return dp[from][0];
}

void dfs2 (int from, int fa) { // 树上差分 
    for (int i = head[from]; i; i = edges[i].nxt) {
        if (edges[i].to == fa) continue;
        dfs2 (edges[i].to, from);
        diff[from] += diff[edges[i].to];
    }
    ans = max(ans, diff[from]);
}

　　

　　

G - Tree Destruction

题意:

一颗n个顶点的树, 可以选择两个顶点a, b一次, 删除从a到b的路径上所有的顶点,

包括本身, 如果a = b则删除这一个顶点, 找到获得连通块最大的个数.

思路:

 

dp[from] 表示从from开始往下选择一条路径删除, 最后能得到的最多连通块

Code:

#include <bits/stdc++.h>
 
using namespace std;
typedef int64_t i64;
const int N = 2e5 + 5;
vector<int> adj[N];
int dp[N], ans = 0, n;

void dfs (int from, int fa) { 
    dp[from] = adj[from].size();
    ans = max(ans, dp[from]);
    for (int to : adj[from]) {
        if (to == fa) continue;
        dfs(to, from);
        ans = max(ans, dp[from] + dp[to] - 2);
        dp[from] = max(dp[from], dp[to] + int(adj[from].size()) - 2);
    }
}

void Solve() {
    ans = 1; 
    cin >> n;
    for (int i = 1; i < n; i++) {
        int from, to;
        cin >> from >> to;
        adj[from].push_back(to);
        adj[to].push_back(from);
    }
    dfs(1, 0);
    cout << ans << '\n';
    for (int i = 1; i <= n; i++) {
        adj[i].clear();
        dp[i] = 0;
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    int t = 1;
    cin >> t;
    while (t--)
        Solve();
    return 0;
}

　　

参考博客:

https://oi-wiki.org/graph/