这场比较guess吧
A.困难数学题
题意:(数学)
计算x ^ x ^ x ^ x的值
思路:
根据异或的结论 x ^ x = 0 可代入式子得到最终结果为0
复杂度:
O(1)
Code:
n = int(input())
print(0)
知识点(拓展):
常用结论:
自反性:
对于任意a满足, a ^ a = 0 && a ^ 0 = a
交换性:
对于任意a 和 b满足, a ^ b = b ^ a
结合性:
对于任意a, b, c满足, (a ^ b) ^ c = a ^ (b ^ c)
B.构造序列
题意:(贪心)
n 个正数 m个负数 正数不能和正数相邻,负数不能和负数相邻 最长能构造多长的序列
思路:
如果要实现最长的序列也就是正负交替实现,很快得到min(n, m) * 2 + (n != m)
复杂度:
O(1)
Code:
#include <bits/stdc++.h>
using namespace std;
void solve() {
int n, m;
cin >> n >> m;
cout << min(n, m) * 2 + (n != m) << '\n';
}
int main() {
cin.tie(0) -> sync_with_stdio(false);
int t = 1;
// cin >> t;
while (t--) {
solve();
}
return 0;
}
C.连点成线
题意:(模拟)
给定一个 n * n 的棋盘和 m 个棋子,每个棋子的坐标为 (x[i], y[i])。如果两个棋子在同一行或同一列,可以连线。
求连上线后最长的那条线的长度,若没有连线则输出 0。
思路:
通过遍历棋子,记录每一行和每一列的最大值和最小值,然后根据这些值计算出最长的连线长度
复杂度:
O(n)
Code:
#include <bits/stdc++.h>
using namespace std;
void solve() {
int n, m;
cin >> n >> m;
vector <int> mi_x(n + 1, n + 1), mx_x(n + 1, 0),
mi_y(n + 1, n + 1), mx_y(n + 1, 0);
for (int i = 0; i < m; i++) {
int x, y;
cin >> x >> y;
mi_x[x] = min(mi_x[x], y);
mx_x[x] = max(mx_x[x], y);
mi_y[y] = min(mi_y[y], x);
mx_y[y] = max(mx_y[y], x);
}
int ans = 0;
for (int i = 1; i <= n; i++) {
if (mx_x[i] > mi_x[i]) {
ans = max(ans, mx_x[i] - mi_x[i]);
}
if (mx_y[i] > mi_y[i]) {
ans = max(ans, mx_y[i] - mi_y[i]);
}
}
cout << ans << '\n';
}
int main() {
cin.tie(0) -> sync_with_stdio(false);
int t = 1;
// cin >> t;
while (t--) {
solve();
}
return 0;
}
D.我们N个真是太厉害了
题意:(贪心 类似于硬币问题(覆盖问题))
判断几个人手中的 ai 个数能否相加表示 n 以内的任意正整数,若可以则输出 'Cool!',否则输出无法表示的最小正整数
思路:
通过依次遍历并累加满足 a[i] <= sum + 1 的星星数量,我们可以扩展可表示的整数范围为 [1, sum],直到找到某个 a[i] > sum + 1,此时 sum + 1 就是无法表示的最小整数
Code:
#include <bits/stdc++.h>
using namespace std;
void solve() {
int n;
cin >> n;
vector <int> a(n);
for (int &i : a) cin >> i;
sort(a.begin(), a.end());
int cur = 0;
for (int i : a) {
if (cur >= i - 1 && cur <= n) {
cur += i;
}
}
if (cur >= n) {
cout << "Cool!\n";
} else {
cout << cur + 1 << '\n';
}
}
int main() {
cin.tie(0) -> sync_with_stdio(false);
int t = 1;
cin >> t;
while (t--) {
solve();
}
return 0;
}
E.折返跑
知识点传送门:https://www.cnblogs.com/BobHuang/p/14979765.html
题意:
将 m - 1 次推杆操作视为在 n - 2 个点的范围内移动,使得左杆和右杆始终保持不重合 保持合法问有多少种推法
思路:
结论为 C(n - 2, m - 1) 是因为问题等价于在 ( n - 2 ) 个点中选择 ( m - 1 ) 个位置进行推杆操作,计算出所有可能的合法推法
Code:
#include <bits/stdc++.h>
using namespace std;
using i64 = int64_t;
constexpr i64 mod = 1e9 + 7, maxn = 1e6 + 5; // 998244353
i64 inv[maxn], f[maxn];
i64 power (i64 a, i64 b) {
i64 res = 1;
for ( ; b > 0; b >>= 1, a = a * a % mod) {
if (b & 1) res = res * a % mod;
}
return res;
}
void init () {
inv[0] = f[0] = 1;
for (int i = 1; i < maxn; ++i) {
f[i] = (f[i - 1] * i) % mod;
inv[i] = power(f[i], mod - 2) % mod;
}
}
i64 C(int n, int k) {
return f[n] * inv[k] % mod * inv[n - k] % mod;
}
void solve() {
int n, m;
cin >> n >> m;
cout << C(n - 2, m - 1) << '\n';
}
int main() {
cin.tie(0) -> sync_with_stdio(false);
int t = 1;
init();
cin >> t;
while (t--) {
solve();
}
return 0;
}
F.口吃
n = 1的时候只有两种情况, 原地和进步
n >= 2的时候
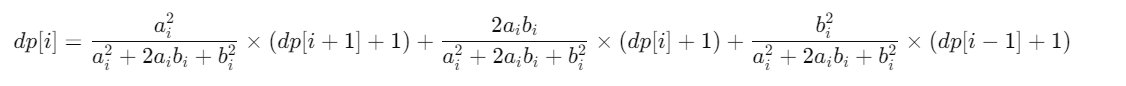
所以我们只要通过化简就可以得到dp[i]的式子
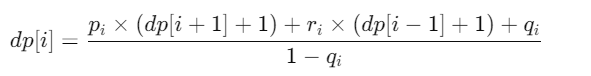
最后从最后的结果推上去即可得到最终答案
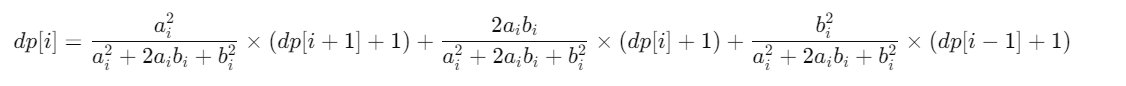
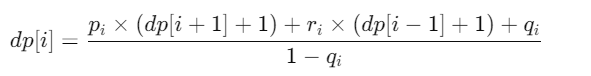


 浙公网安备 33010602011771号
浙公网安备 33010602011771号