论文阅读 | ECA-Net

ECA-Net

TJU CVPR'20

Abstract

ECA-Net 是基于 SE-Net 的扩展，其认为 SE block 的两个 FC 层之间的维度缩减是不利于学习注意力权重的，学习过程应该与原始通道直接一一对应。作者做了一系列实验来证明在 Att Block 中保持 Channel 数不变的重要性。

Ablation Study

保持 Squeeze 部分不变，本文对比了多种 Excitation 设计。考虑如下实验。

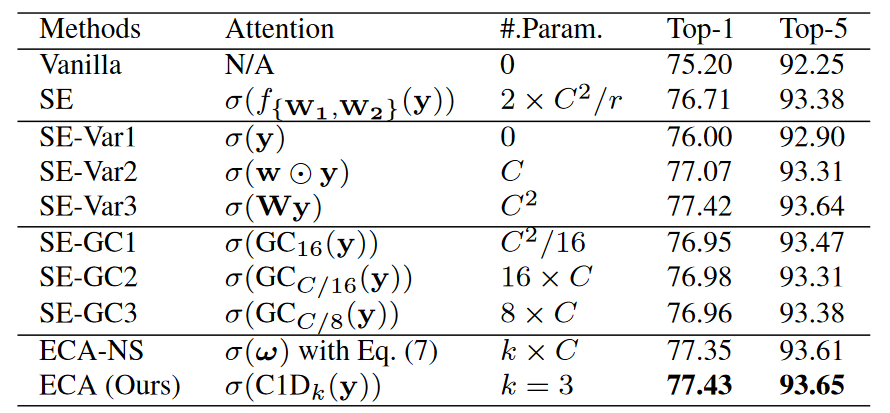
其中，\(f_{\{\mathbf{w}_L\}}(\cdot)\) 代表一个 \(L-1\) 隐藏层的感知机，以 \(L=2\) 为例，可写作

\[f_{\{ \mathbf{w}_1, \mathbf{w}_2\}}( \mathbf{y}) = \mathbf{W}_2 \mathrm{ReLU}( \mathbf{W}_1 \mathbf{y}) \tag{1} \]

\(\sigma\) 代表 Sigmoid，\(\text{GC}_k\) 与 \(C1D_k\) 分别代表 kernel size 为 \(k\) 的 Group Conv 和 Conv1D。此外，ECA-NS 的计算方式较特殊，引入一个稀疏的全连接矩阵 \(\{w_i^{j}\} \in \mathbb{R}^{C \times C}\)，通过下式计算注意力权重 \(\omega\)：

\[\omega_i = \sigma \left( \sum_{j=1}^k w_i^j y_i^j \right), \quad y_i^j \in \Omega_i^k, \tag{2} \]

where \(\Omega_i^k\) indicates the set of \(k\) adjacent channels of \(y_i\). ECA-NS 的注意力计算方式可视为 stride 之间产生重叠的 Group Conv，或是某种卷积核随通道位置变化而变化的特殊卷积。

不考虑通道位置，对式 (2) 进行简化

\[\omega_i = \sigma \left( \sum_{j=1}^k w^j y_i^j \right), \quad y_i^j \in \Omega_i^k, \tag{3} \]

此时 ECA-NS 退化为一个 kernel size 为 \(k\) 的 Conv1D 操作，即

\[\omega = \sigma(C1D_k(\mathbf{y})) \tag{4} \]

式 (4) 即 ECA-Net 的最终形式。下文进行讲解。

Comparasion of Various \(\mathbf{F}_{ex}\)

分析上表，得出如下结论。

1. Vanilla 为原始的 \(\mathbf{F}_{tr}(\cdot)\)，在 ECA-Net 中为某个卷积层输出的特征图。SE 为原始 SE-Net，可知 CA 模块确实带来了性能提升。
2. SE-Var1 使用了非参数化的注意力函数 \(\sigma(\cdot)\)，对比 Vanilla 与 SE-Var1 可知，直接将 Squeeze 层压缩得到的特征表示 \(\mathbf{y}\) 输入 Sigmoid，仍有一定的性能提升。
3. 在 SE-Var1 基础上，SE-Var2 使用一个注意力向量 \(\mathbf{w}\) 与 \(\mathbf{y}\) 做点积，不考虑通道间交互，独立学习每个 Channel 的注意力权重。尽管参数更少，此时的性能已经超过 SE-Net。这表明通道压缩是无效的，维持通道数比考虑 Channel 之间的非线性依赖关系更加重要。
4. SE-Var3 应用了一层 FC，性能超越没有跨通道信息交互的 SE-Var2。证明让 CA 学习通道之间的相关性是必要的。

以上实验已经证明观点，即不应该进行通道缩减。接下来的实验则在参数量与性能之间寻求平衡。

1. 考虑 SE-GC1，SE-GC2，SE-GC3，使用分组卷积降低参数量，但性能提升相较于 SE 并不显著。这可能是 Group Conv 忽略了组间依赖关系所致。
2. ECA-NS 解决了不同 Group 间的信息隔离问题，性能相比 SE-GC3 提升。
3. ECA 在 ECA-NS 基础上使用了共享权重，降低参数量的同时，性能再次提升。

Proposed Method

Overview

根据上文讨论，ECA-Net 最终使用一个自适应 kernel size 的快速 1D 卷积作为 Excitation Block 进行通道注意力计算。

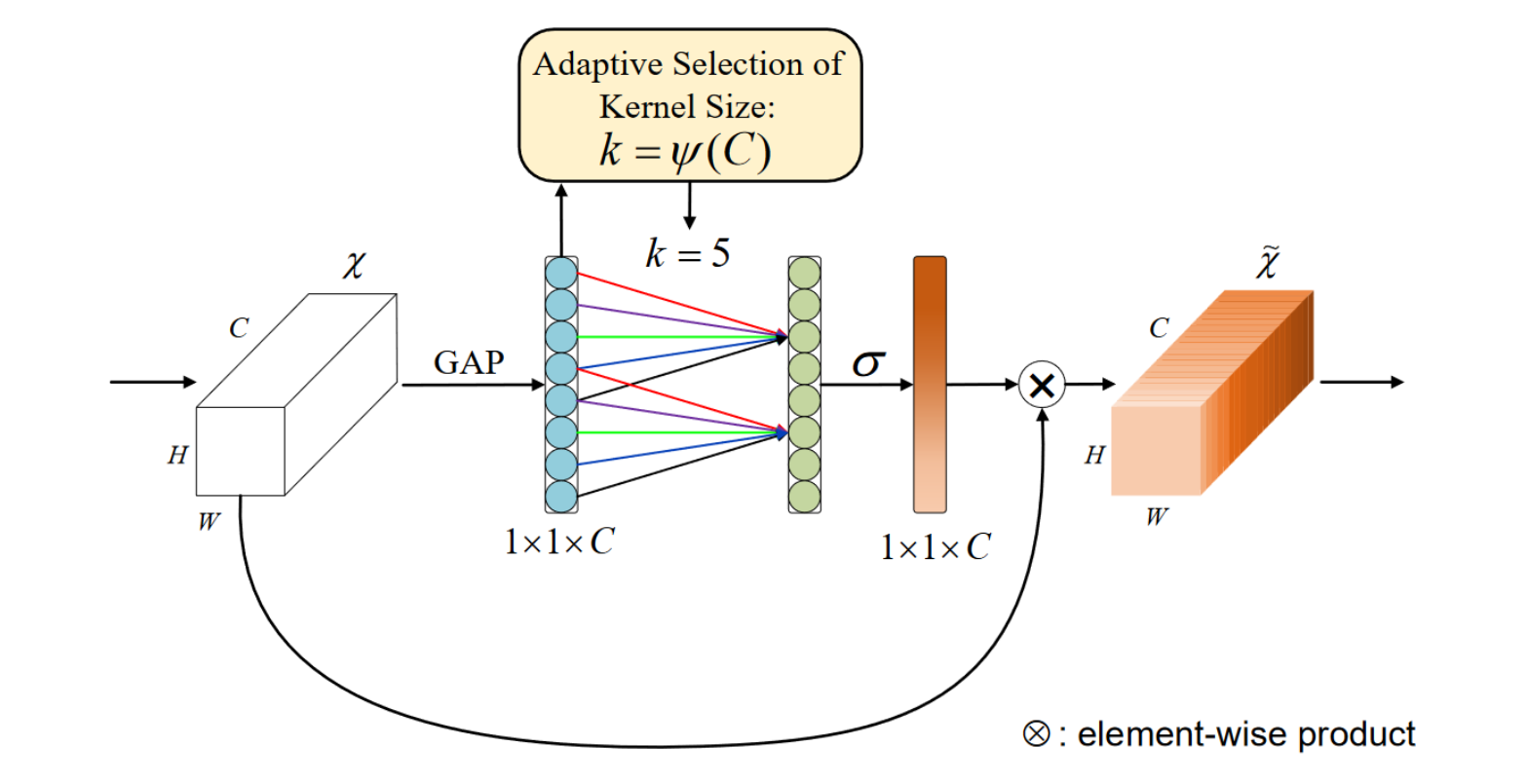
其中，通道数 \(C\) 与 kernel size \(k\) 的关系可建模如下

\[C = \phi(k) = 2^{(\gamma * k - b)} \tag{5} \]

从而

\[k = \psi(C) = \left| \frac{\log_2(C)}{\gamma} + \frac{b}{\gamma} \right|_{\text{odd}} \tag{6} \]

伪代码

Summary

现有的通道注意力方法尽管提高了性能，但不可避免的增加了模型的复杂性。为了克服性能和复杂度之间的矛盾，本文提出了一种有效的通道注意模块 (ECA-Net)，该模块只涉及少量参数，通过快速 1D 卷积进行通道注意力计算，同时具有明显的性能增益。作者认为，降维会对通道注意力预测产生副作用，并且 捕捉所有通道的依赖关系是低效和不必要的。 因此应避免通道缩减，同时只保持适当的跨通道交互，保持性能的同时，也能显著降低模型复杂性。

总结而言，所提出的 ECA-Net 有如下优势。

1. 避免特征维度的缩减
2. 增加 Channel 间信息交互
3. 只引入很少的参数，同时保持较好的性能