CF合集

2130. CodeForces Round 1040（Div. 2）

过题： 3/8 排名： 5622

状态奇差的一场，每一步都做了错误的选择。

A 没仔细写，WA了之后没有查哪里错了就慌着去开 B ，结果 B 看漏了零一二都有的条件，写了半天讨论。D 题也拿着假结论写了半天，发现样例都过不了，哈哈破防了。

A. Submission is All You Need

手玩发现只有选 \(\{0\}\) 和 \(\{0,1\}\) 时操作二更有收益。因此统计 \(0\) 的个数就行了。

时间复杂度 \(\mathcal O(n)\) 。Code.

B. Pathless

注意到 \(0\) 和 \(1\) 不能相邻放。不然可以在这两格间随便刷。

因此如果有答案，答案应该是 00..022..21..11 形式（将 \(2\) 放在 \(0\) 或 \(1\) 中不会带来本质不同的相邻组合）。接着判断是否有答案。

设 \(\delta = s - \sum_{i = 1}^{n}a_i\) 。

• 若 \(\delta < 0\) ，随便放。
• 若 \(\delta =0\) ，无解。
• 若 \(\delta=1\) ，按照上述方法放就行。
• 若 \(\delta\geq2\) ，总能通过在 02 或者 21 之间多刷出 $\delta $。所以无解。

被自己的读题习惯害惨了。赛时没看见零一二都有，讨论了好多。

时间复杂度 \(\mathcal O(n)\)。Code.

C. Double Perspective

首先发现，如果 \(a<b<c\) ，现有 $(a, c) $ 和 \((b, c)\) ，那么删去后者不改变 \(f\) 值且有可能使 \(g\) 值减小。因此删去它一定不劣于保留它。所以我们对每个数都只保留以它为右端点的线段中最长的一个。

然后发现这样的取舍方式下，图中根本就没有环了，即 \(g=0\) 。同时 \(f\) 值没有改变。这就是最优方案。

时间复杂度视实现为 \(\mathcal O(n)\) 或 \(\mathcal O(n\log n)\) 。笔者的实现为后者。Code.

---

2131. CodeForces Round 1042（Div. 3）

过题： 5/8 排名： 910

状态依旧很差，F 和 G 本应都做出来，结果双双弃掉。

A. Lever

显然操作是随机序还是按照顺序并不影响答案。直接线性扫一遍，统计操作 \(1\) 进行的次数即可。

时间复杂度 \(\mathcal O(n)\)。Code.

B. Alternating Series

负数小于等于 \(-1\) ，因此被夹在两负数间的正数至少为 \(3\)，两端的正数至少为 \(2\) 。

要使绝对值序列字典序最小，答案一定是 -1 3 -1 ... 3 -1（奇数） 或 -1 3 -1 ... 3 -1 2（偶数） 的形式。

时间复杂度 \(\mathcal O(n)\)。Code.

C. Make it Equal

观察易知，\(a\) 能转化到 \(b\) 的条件是：$a\equiv b\pmod k $ ，或者 \(a + b \equiv 0 \pmod k\) 。

考虑用 map 记录模意义下各数对应的原数数量，挨个检查即可。

时间复杂度 \(\mathcal O(n\log n)\)。Code.

D. Arboris Contractio

一般来说，菊花图一定有且仅有一个花心，考虑这个花心是谁。

先假定我们已确定了这个花心。那么最优的操作流程即：每次令该花心为路径一端，再依次选择初始度为 \(1\) 的所有结点为路径另一端（若初始距离即为 \(1\) ，可跳过该步）。

设初始度为 \(1\) 的结点数量为 \(n_0\)，其中与花心距离为 \(1\) 的结点数量为 \(n_1\) 。则答案为：\(\min\{n_0 - n_1\} = n_0 - \max{n_1}\) . 统计每个结点的 \(n_1\) 取 \(\max\) 即可。

此外，注意特判仅两个结点的 Corner Case。

时间复杂度 \(\mathcal O(n)\)。Code.

E. Adjacent XOR

首先，由于每个数只能操作一次，变了之后不能恢复。因此每个数最多 \(a_i\) 和 \(b_i\) 两种形态。

先趁右侧的数还未改变，按顺序将能修改的 \(a_i\) 都进行修改。然后再倒序操作，在右侧的数已改变的情形下尝试修改。一旦存在修改不成的情况，判断为 NO，否则为 YES。

时间复杂度 \(\mathcal O(n)\)。Code.

题外话，一开始以为这题每个数可以进行多次操作。这样的做法是利用异或后缀倒序处理，好像比原题更有说法一些。

*F. Unjust Binary Life

如果存在一条从 \((1,1)\to (x, y)\) 的全 \(0\) 路径，则必然产生一系列连等关系最终推得 \(a_1...a_x, b_1...b_y\) 全部相等。比如下图中 \(a_1 \oplus b_1 = a_2\oplus b_1 = a_2\oplus b_2 = 0\) 可以推得：\(a_1 = b_1 = a_2 = b_2=…\) 。

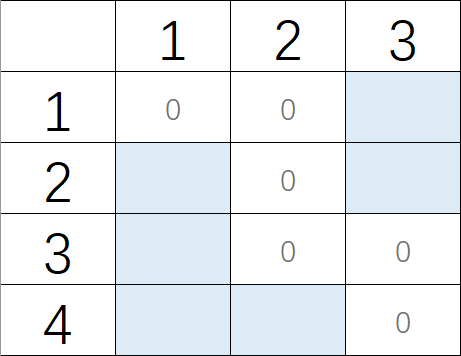
所以可以得出：

\[f(x, y)=\min\{\sum_{i = 1}^x a_i +\sum_{i = 1}^y b_i,\quad x + y -(\sum_{i = 1}^x a_i + \sum_{i = 1}^y b_i)\} \]

假定有：

\[\sum_{i = 1}^x a_i +\sum_{i = 1}^y b_i\leq x + y -(\sum_{i = 1}^x a_i + \sum_{i = 1}^y b_i) \]

分离变量可以得到：

\[2\sum_{i = 1}^x a_i - x\leq y - 2\sum_{i = 1}^y b_i \]

固定 \(x\)，枚举 \(y\) 。上式符合时， \((x, y)\) 对答案的贡献是 \(\sum_{i = 1}^x a_i +\sum_{i = 1}^y b_i\) ，否则为 \(x + y -(\sum_{i = 1}^x a_i + \sum_{i = 1}^y b_i)\).

因此我们将所有 \(y\) 按照 \(y - 2\sum_{i = 1}^y b_i\) 排序，对排序后的两种贡献分别做前缀和。这样在枚举 \(x\) 时便可以二分找到分界点，根据前缀和快速得到这一行对答案的总贡献。

时间复杂度 \(\mathcal O(n\log n)\)。Code.