qy_蓝桥杯编程系列_编程23 函数之和

编程23 函数之和

这题我原以为是很复杂的，看到解题过程倒有点啼笑皆非，让我想起来和初中的知识点蛮像的

一、题目简介

  可以看到这题让我们求的是函数f(k)的输出，这个函数f(k)具体来说就是1~k中数字任意组合，加起来和为k的组合个数共有多少个，包括k作为单独的一个数算作一个组合，这个组合按题目要求是以数组形式呈现，这个最终的个数就是函数f(k)的输出了。
  不知道大家看到这个题能不能很快想出解决方法呢，我之前看这题的时候以为要经过一系列复杂的转换，或者如何巧妙的方法，而最后的解决方法也确实称得上巧妙，就是比我想象的少很多。这题我们先放代码：

import math
k = int(input())

def arrays_sum(n):
  return int(math.pow(2,n-1))

print(arrays_sum(k))

  没错这就是全部代码了，如果不写函数形式的话还可以更短，那么为什么简单的2的指数就可以计算出结果呢？其实就是大家可能初中学过的，简单的插空格算可能性（这种方法有名字吗我不记得了这是我编的hhh将就理解吧），我们通过图片配合会更好理解一点。
  以k=3为例，正常求这题的思路就是依次列举，从小到大的话就是三个1，一个1和一个2再掉转顺序（数组形式顺序不一样属于不同数组），最后是一个3，求出函数f(3)=4，那么我们可以这样用图表示出来：

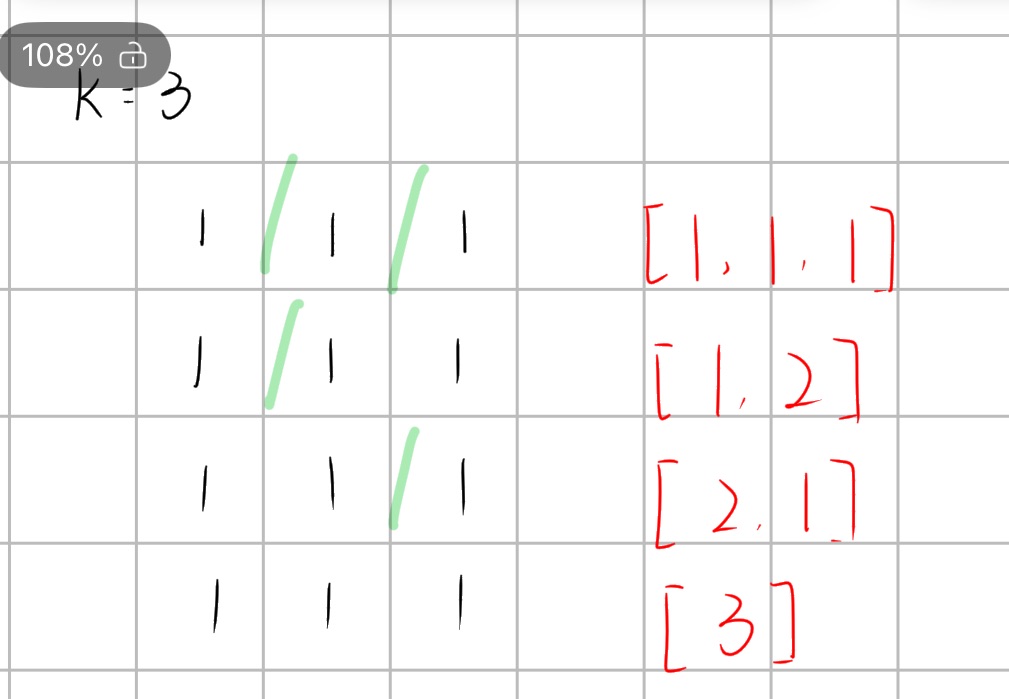
  关键就在这张图的表现形式上，我们发现如果k=3可以这样表示，k=4是不是也可以，

  好的两个例子摆出来的话规律就比较明显了，求的函数值就等于在k个1中间插入隔板的所有可能性，这种插入隔板的解法大家都应该学过吧，没学过也不难理解，k个1共有(k-1)个空隔，每个空隔仅有插入隔板和不插入隔板两个选择，每个空隔的所有可能性都要与其他空隔的所有可能性相乘，那所有的可能性不就是2的（k-1）次方了。
  本题解法还挺有趣的，代码也比较简单，就是比较考验脑筋诶。不过也是属于做过就不可能再错的题目还是比较友好的~