qy_蓝桥杯编程系列_编程22 不停的上课

编程22 不停的上课

本题要用到二维数组，以及时间轴的巧妙运算，虽然比较难想到我觉得，但写过一次之后就大概率不会有问题啦~

一、 题目简介

  这题看起来还是比较简单的，手算的话大家都会，但是要如何用代码计算呢，可能会比看上去复杂一点，因为这n行数据每一行都要相互比较，且不拘泥于同列的比较。如样例中的第一、二行，可以看到第二个时间段开始的比第一个时间段晚（1000>800），再比较第一个时间段的结束时刻1000（第2列）和第二个时间段的起始时刻1000（第一列），两个相等得出两个时间段无交集，此时再用一维数组就没办法做到了，所以我们需要将输入的数组存储在二维数组中，再进行如上述的比较得出交集。

二、 解题方法

2.1 二维数组存储数据

  因为是动态的输入存储，所以可以用一个循环来解决
代码演示

arr = []
for i in range(n):
  a, b = map(int, input().split())
  arr.append([a, b])

当然也有很多别的写法可探索，比如将a，b先转换为列表形式再添加到arr数组，或者将这些简写成一行等等：

arr = [list(map(int, input().split())) for _ in range(n)]

2.2 求交集

  集合求交集大家都会，但是这样的n行 [起始时刻，结束时刻] 的数据，求任意两行数据的交集，输出最大交集，还是需要发现一点系统性的规律来帮我们通过算法计算。

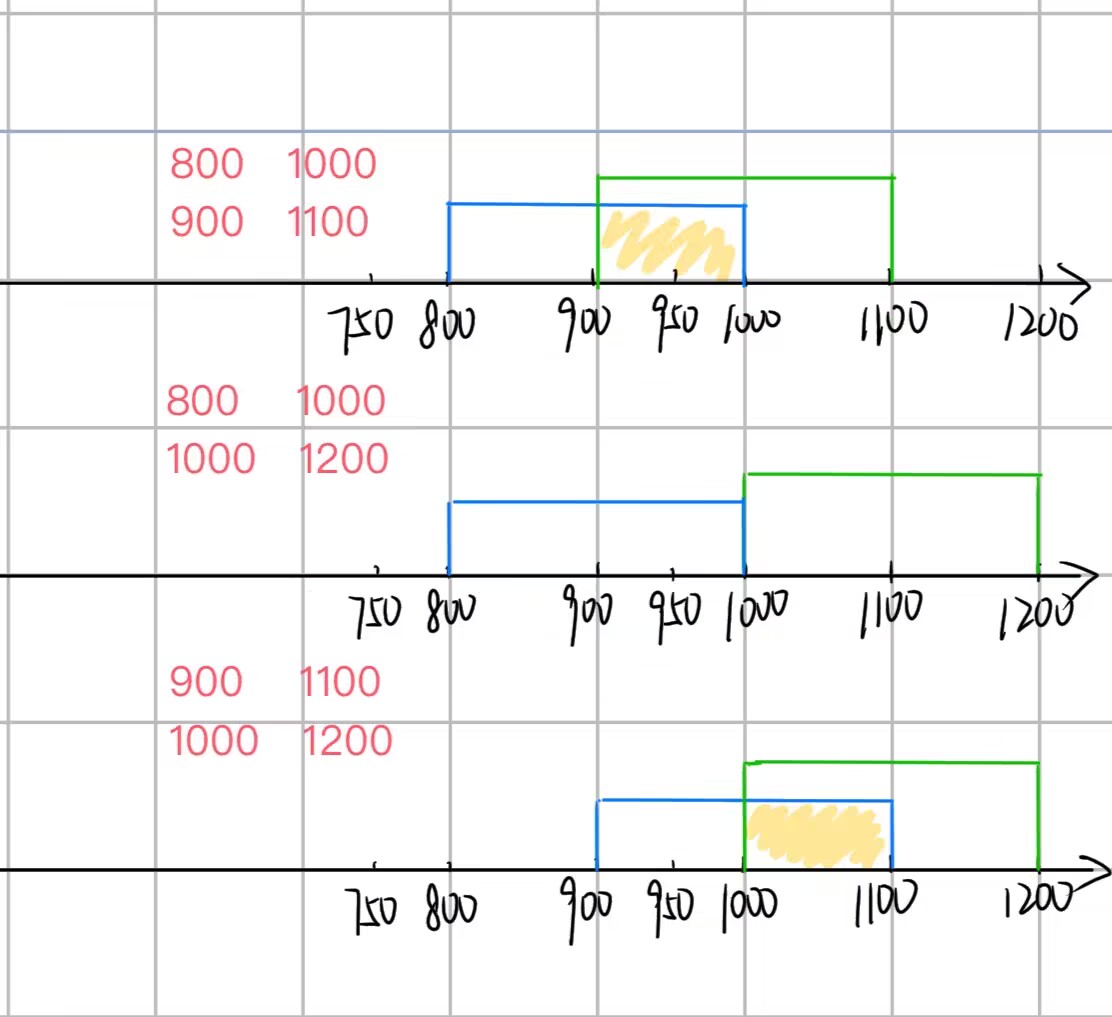
  如图所示，以前三组数据为例，想要两个时间段有交集，两组相比较的数据中，起始时刻相比较更大的数据，与结束时刻相比较更小的数据间可以组成一个正向时间段。如[800,1000]和[900,1100]两组数据相比，起始时刻相比更大的数据是900，结束时刻相比更小的数据是1000，而1000大于900，所以在新的时间段内，依旧以900为起始时刻，1000为结束时刻，[900,1000]的时间段是正向有效存在的，所以我们最初比较的[800,1000]和[900,1100]是存在交集且交集时间为（1000-900）=100的。
  那么逻辑梳理出来写代码就比较简单了，不过这些具体体现在代码中还需注意的是，如此计算需套两层循环，一层n行数据的遍历，第二层是每行数据都要与除它以外的所有行数进行比较，不过两行对比过后无需重复比较，所以直接从上往下顺位比较所遍历到的行数数据之下的数据即可，具体代码如下：

intersection = 0
for i in range(n):
  for j in range(i+1, n):
    inter_start = max(arr[i][0],arr[j][0])
    inter_end = min(arr[i][1],arr[j][1])

    intersection = max(intersection,inter_end - inter_start)

  以上代码中inter_start和inter_end是交集数据的起始时刻与结束时间，交集时间计算为inter_end - inter_start，intersection为最大交集，每次交集的计算需与之前的最大交集相比较，取更大值赋给intersection
  以下图简单举例就是第一遍遍历到[800,1000]，进入第二层循环，将[800,1000]依次与下面的[1000,1200]、[900,1100]、[200,950]、[750,800]进行比较，分别计算[800,1000]与这些数据交集多少，如第二层循环第一次遍历到[1000,1200]，则 inter_start就是800与1000比较更大的数，得到1000，inter_end就是1000与1200比较更小的数得到1000，新的交集数据为]1000,1000]，交集时间为inter_end-inter_start得到0，intersection就等于0。以此类推第二层第二次遍历计算的交集为100，100大于0则新的intersection为100，两层遍历结束即可得到最大交集时间

完整代码

n = int(input())
arr = []
for i in range(n):
  a, b = map(int,input().split())
  arr.append([a, b])

intersection = 0
for i in range(n):
  for j in range(i+1, n):
    inter_start = max(arr[i][0],arr[j][0])
    inter_end = min(arr[i][1],arr[j][1])

    intersection = max(intersection,inter_end - inter_start)

print(intersection)