数据结构018_赫夫曼树

赫夫曼树名字看起来很难，其实蛮简单的。我记得为大学的时候就很爱做赫夫曼树，因为很容易掌握而且做对。笑了。

一、赫夫曼树

1）给定n个权值作为n个叶子结点，构造一棵二叉树，若该树带权路径(wpl)达到最小，称这样的树为最优二叉树，也叫赫夫曼树(Huffman Tree)。

2）赫夫曼树是带权路径长度最短的树，权值较大的节点离根节点近。

二、概念

1）路径和路径长度：在一棵树中，从一个节点往下可以达到的孩子或孙子结点之间的通路称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1，则从根结点到第L层节点的路径长度为L-1。

2）结点的权及带权路径长度：若将树中结点赋给一个有着某种含义的数值，则这个数值称为该结点的权。结点的带权路径长度为：从根结点到该节点之间的路径长度与该结点的权的乘积。

3）树的带权路径长度：树的带权路径长度规定为，所有叶子结点的带权路径长度之和，记WPL(weighted path length)。

4）WPL最小的就是赫夫曼树。

三、创建赫夫曼树思路及代码实现

数列{13,7,8,3,29,6,1}，转成一棵赫夫曼树。

步骤：

1）从小到大进行排序，将每个数据作为一个结点，每个节点看成一棵最简单的二叉树。

2）取出根结点权值最小的两棵二叉树。

3）组成一棵新的二叉树。新树根结点的权值是前面两棵二叉树根结点权值的和。

4）再将这颗新的二叉树，以根结点的权值大小，再次排序。不断重复1234步骤，直到数列中所有的数据都被处理，就得到一棵赫夫曼树。

 

 

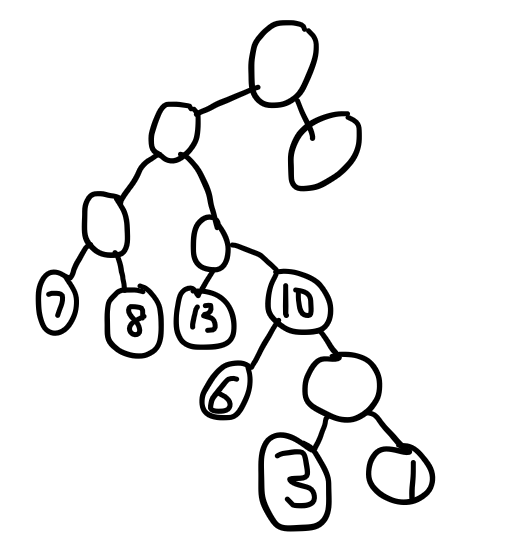
代码实现：

 

package com.njcx.tree;

import java.util.ArrayList;
import java.util.Collections;
import java.util.List;

public class HuffmanTree {

    public static void main(String[] args) {
        int arr[] = { 13, 7, 8, 3, 29, 6, 1 };
        Node root = createHuffmanTree(arr);

        // 前序遍历一下创建出的赫夫曼树看看对不对
        preOrder(root);
    }

    /**
     * 创建赫夫曼树的方法
     * @param arr 需要创建成赫夫曼树的数组
     * @return 创建好的赫夫曼树的root结点
     */
    public static Node createHuffmanTree(int[] arr) {
        // 数组本身不支持排序,ArrayList支持排序,为了操作方便
        // 1.遍历arr数组
        // 2.将arr的每个元素构成一个Node
        // 3.将Node放到ArrayList中
        List<Node> nodes = new ArrayList<Node>();
        for (int value : arr) {
            nodes.add(new Node(value));
        }

        // 我们处理的过程是一个循环的过程,直到nodes中只有一个元素
        while (nodes.size() > 1) {
            // 排序 从小到大 (这个取决于compareTo()怎么写的)
            Collections.sort(nodes);

            System.out.println("nodes=" + nodes);

            // 取出根结点权值最小的两棵二叉树
            // (1) 取出权值最小的结点(二叉树)
            Node leftNode = nodes.get(0);
            // (2)
            // 取出权值次小的结点【这里说明,remove后,list下标是不会改变的,node[1]还是node[1],没有变成node[0]】
            Node rightNode = nodes.get(1);
            // (3) 构建一棵新的二叉树
            Node parent = new Node(leftNode.value + rightNode.value);
            parent.left = leftNode;
            parent.right = rightNode;
            // (4) 从ArrayList中删除处理过的二叉树
            nodes.remove(leftNode);
            nodes.remove(rightNode);
            // (5) 将parent加进nodes
            nodes.add(parent);
            // System.out.println("第一次处理后：" + nodes);
        }
        // 返回赫夫曼树的头root
        return nodes.get(0);
    }

    // 编写一个前序遍历的方法
    public static void preOrder(Node root) {
        if (root != null)
            root.preOrder();
        else
            System.out.println("空树");
    }

}

/**
 * 结点类Node,存放数据和权值 为了让Node 对象排序 Collections集合排序 实现Comparable接口
 * 
 * @author 抱金子
 */
class Node implements Comparable<Node> {
    int value;// 结点权值
    Node left;// 指向左子结点
    Node right;// 指向右子结点

    public Node(int value) {
        this.value = value;
    }

    @Override
    public String toString() {
        return "Node [value=" + value + "]";
    }

    @Override
    public int compareTo(Node o) {
        /*
         * Compares this object with the specified object for order. Returns a
         * negative integer, zero, or a positive integer as this object is less
         * than, equal to, or greater than the specified object.
         * 将此对象与一个特定的有序对象o进行比较，小于o返回一个负数，大于o返回一个正数，等于o返回一个0.
         */
        // 表示从小到大排序【√】
        return this.value - o.value;
    }

    // 前序遍历
    public void preOrder() {
        System.out.print(this.value+",");

        if (this.left != null) {
            this.left.preOrder();
        }

        if (this.right != null) {
            this.right.preOrder();
        }
    }

}