《人工智能：线代方法》第二部分问题求解通过搜索进行问题求解(2)

人工智能中的搜索策略大体分为两种：无信息搜索和有信息搜索。
无信息搜索是指我们不知道接下来要搜索的状态哪一个更加接近目标的搜索策略，因此也常被成为盲目搜索；
而有信息搜索则是用启发函数f（n）来衡量哪一个状态更加接近目标状态，并优先对该状态进行搜索，因此与无信息搜索相比往往能够更加高效得解决问题。

无信息搜索算法不提供有关某个状态与目标状态的接近程度的任何线索。
盲目(无信息)搜索策略只使用可用的信息在问题定义中.

广度优先搜索
代价一致搜索
深度优先搜索
深度受限搜索
迭代加深搜索
双向搜索

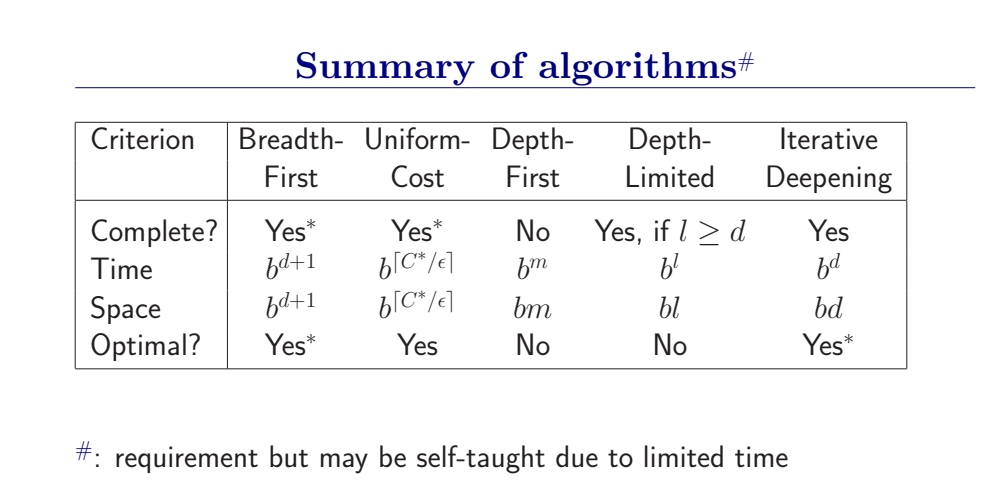
这些搜索策略是以节点扩展的次序来分类的（宽度优先，一致代价，深度优先，深度受限，迭代加深，双向搜索）。要衡量一个搜索策略的好坏，我们需要从四个方面对其进行判断：完备性、时间复杂度、空间复杂度和最优性。因此以下通过这四个方面来比较常见搜索策略之间的优劣。

3.4.1 广度优先搜索

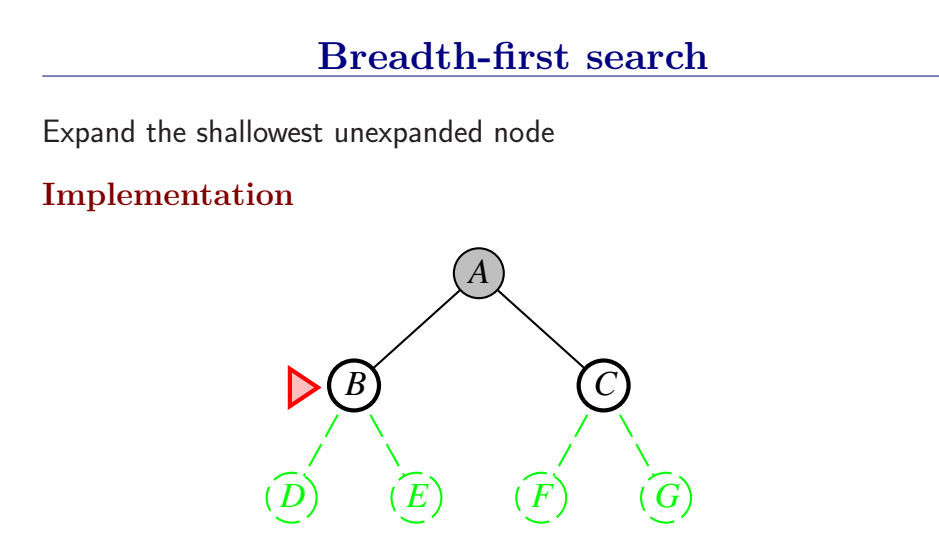
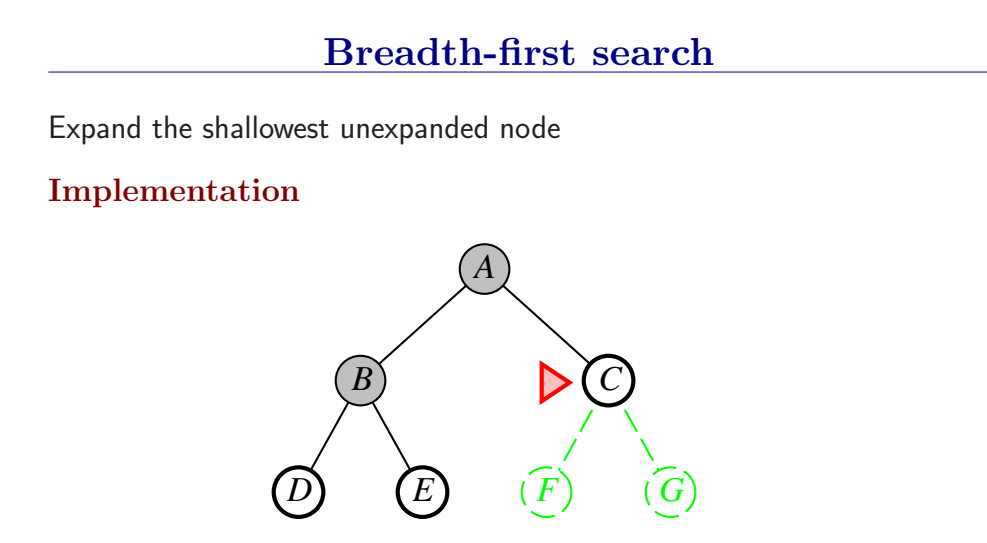
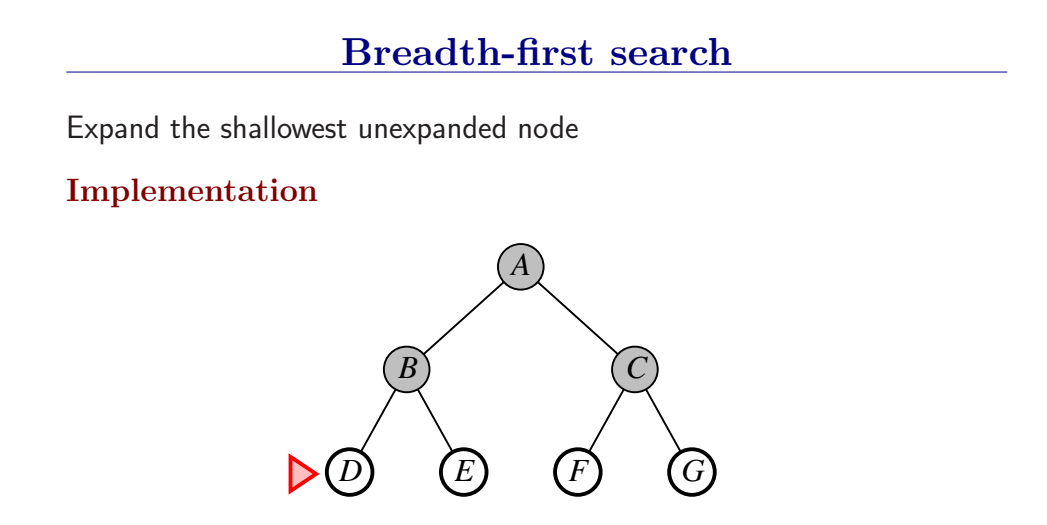
宽度优先搜索是一般图搜索算法的一个实例，每次总是扩展深度最浅的节点，这可以通过将边缘组织成FIFO队列来实现（即，新节点加入到队列尾，浅层的老节点会在深层节点之前被扩展）。

性能：是完备的（只要有解，肯定能搜到。当然，前提是最浅的目标节点处于一个有限深度d，分支因子b也是有限的）BFS找到的永远是最浅的目标节点，但不一定最优，只有当路径代价是基于节点深度的非递减函数时，BFS是最优的（最常见情况是所有行动要花费相同的代价）。
假设每个状态都有b个后继状态，解的深度为d，那么时间复杂度就是 $O({b}^{d})$ ，空间复杂度也是 $O({b}^{d})$ 。这种指数级的复杂度就太大了。
（一般而言，指数级别复杂度的搜索问题不能用无信息的搜索算法求解，除非是规模很小的实例）

首先扩展根节点，然后扩展根节点的所有后继，接着再扩展它们的后继，从而一层一层的对节点进行扩展。
BFS是一个简单的搜索策略，在搜索过程中会对所有状态进行遍历，因此它是完备的；
假设搜索树每个节点有b个后继，深度为d，则时间复杂度和空间复杂度均为O(bd)；
最后考虑最优性，因为我们总会在最浅那一层找到目标状态，因此当且仅当每一步的代价都一致的时候，BFS可以得到最优解。

代码实现

"""
搜索
创建问题类和问题实例，并通过调用各种搜索函数来解决它们。
"""
import sys
from collections import deque
from utils import *

class Problem:
	def __init__(self, initial, goal=None):
		self.initial = initial
        self.goal = goal
    def action(self, state):
		raise NotCodeError
    def result(self, state, action):
		raise NotCodeError
    def is_goal(self, state):
		if isinstance(self.goal, list):
            return is_in(state, self.goal)
        else:
			return state == self.goal
    def path_cost(self, c, state1, action, state2):
		return c + 1
    def value(self, state):
		raise NodeCodeError

class Node:
	"""搜索树中的节点"""
    def __init__(self, state, parent=None, action=None, path_cost=0):
		self.state = state
        self.parent = parent
        self.action = action
        self.path_cost = path_cost
        self.depth = 0
       	if parent:
			self.depth = parent.depth + 1
    def __repr__(self):
		return "<Node {}>".format(self.state)
    def __lt__(self.node):
		return self.state < node.state
    def expand(self, problem):
		return [self.child_node(problem, action)
               for action in problem, action]
    def child_node(self, problem, action):
		next_state = problem.result(self.state, action)
        next_node = Node(next_state, self, action, problem.path_cost(self.path_cost, self.state, action, next_state))
    def solution(self):
		return [node.action for node in self.path()[1:]]

	# class Node continued
	def path(self):
		node, path = self, []
        while node:
			path_back.append(node)
            node = node.parent
        return list(reversed(path_back))
    def __eq__(self, other):
		return isinstance(other, Node) and self.state == other.state
    def __hash__(self):
		return hash(self.state)

"""
BFS
通过调用函数实现伪代码
"""
def breadth_first_search(problem):
	frontier = deque([Node(problem.initial)]) # FIFO queue
    while frontier:
        node = frontier.popleft()
        if problem.is_goal(node.state):
			return node
        frontier.extend(node.expand(problem))
   	return None

3.4.2 Dijkstra算法或一致代价搜索

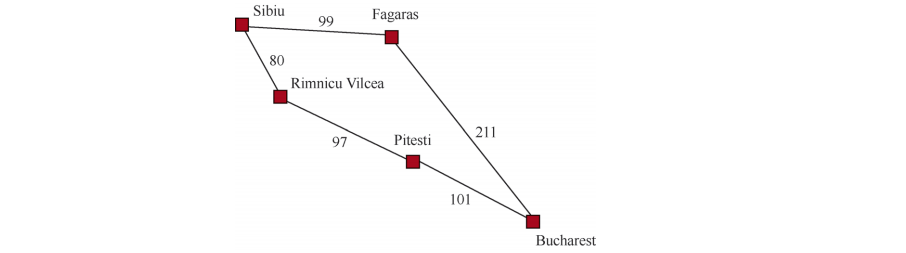
一致代价搜索扩展的是路径消耗g(n)（从初始状态到当前状态的路径耗散）最小的节点n。（可以通过将边缘节点组织成按g值排序的队列来实现）

一致代价搜索和宽度优先搜索的区别：

1）目标检测应用于节点被选择扩展时，而不是在节点生成的时候。原因：一致代价搜索希望在替换代价更小的节点后再确认解；
2）如果边缘中的节点有更好的路径到达该节点，那么会引入一个测试。

性能：是最优的。如果每一步的代价都大于等于某个小的正常数，那么就是完备的。

一致代价的复杂度较高： $O(b^{1 + [C^{*}/e]})$ .
,其中 $C^{*}$ 是最优解的代价，每个行动的代价至少为e，所以最坏情况下，这个复杂度要比BFS的复杂度 $b^{d}$ 大的多。（因为一致代价搜索在探索包含代价大的行动之前，经常会探索代价小的行动步骤所在的很大的搜索树）当所有单步耗散都相等时，复杂度变为 $b^{d+1}$ 。这种情况下，由于一致代价搜索和BFS的第一个区别，一致代价搜索会在深度d上做更多无用功（因为他是在选择节点的时候才判断是不是目标达到）。

在BFS的基础上，一致代价搜索不在扩展深度最浅的节点，而是通过比较路径消耗 $g(n)$ ，并选择当前代价最小的节点进行扩展，因此可以保证无论每一步代价是否一致，都能够找到最优解。

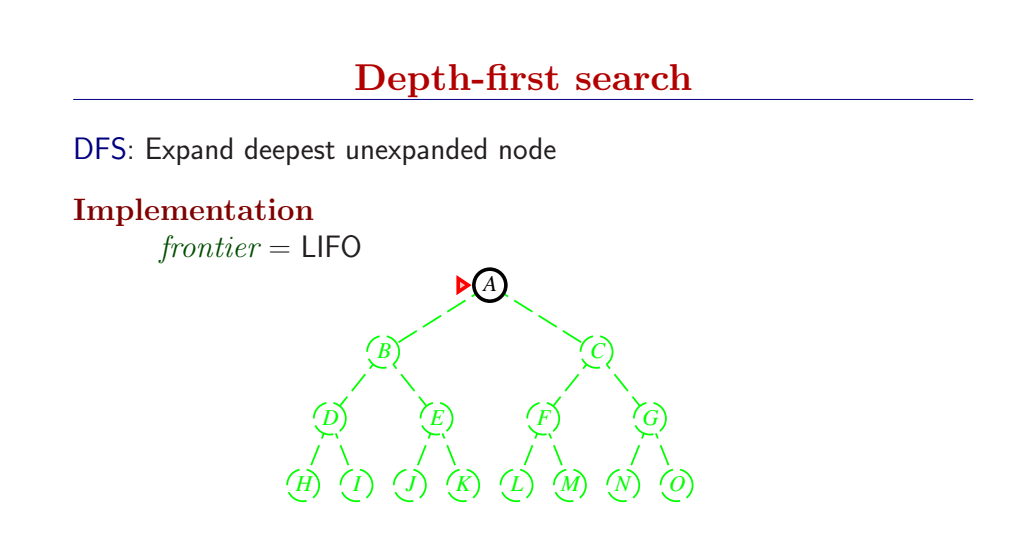
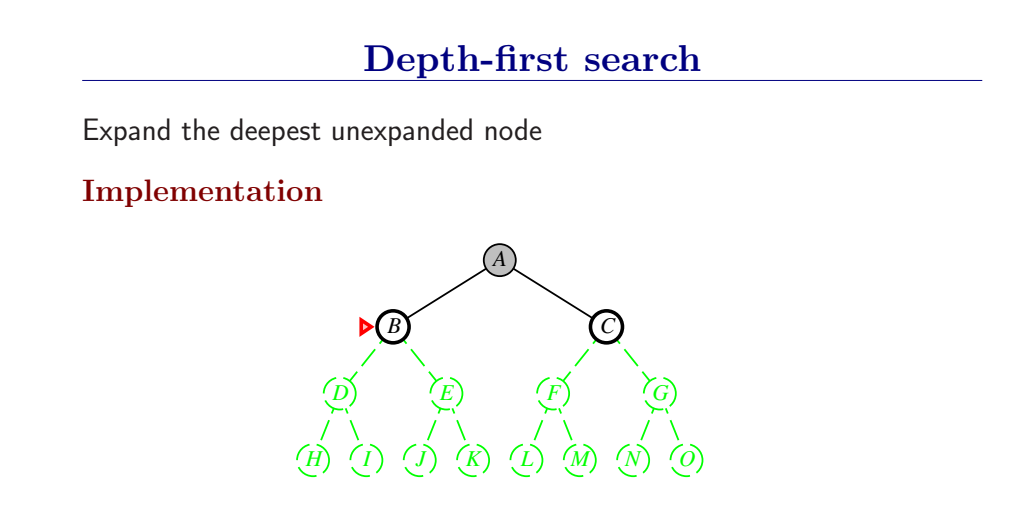
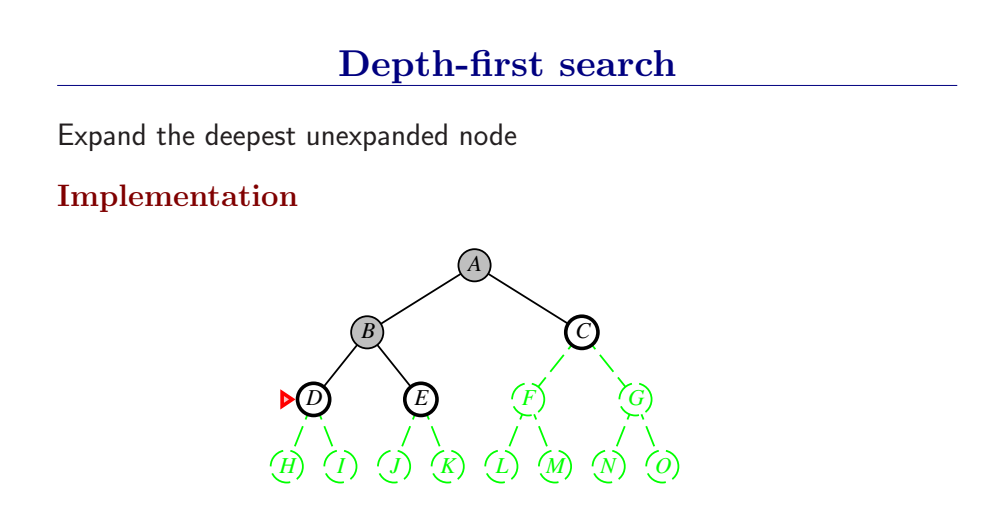
3.4.3 深度优先搜索和内存问题

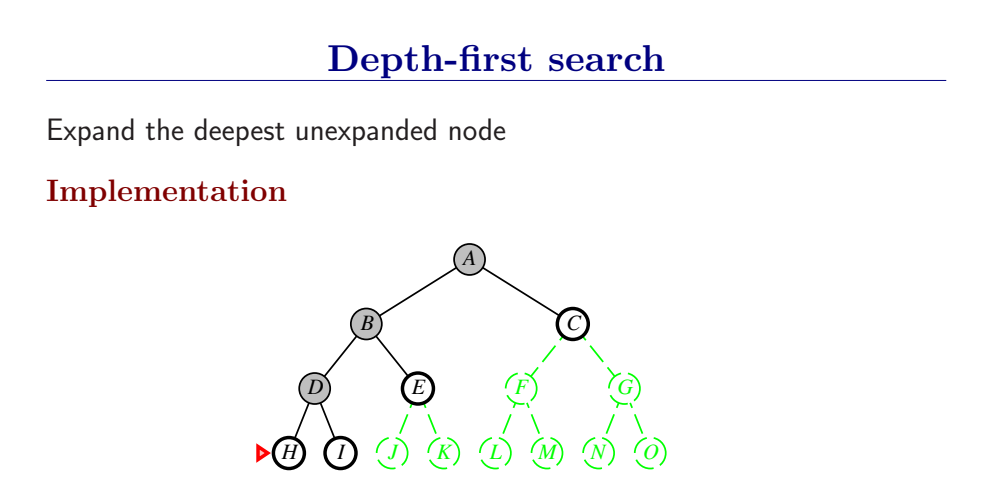
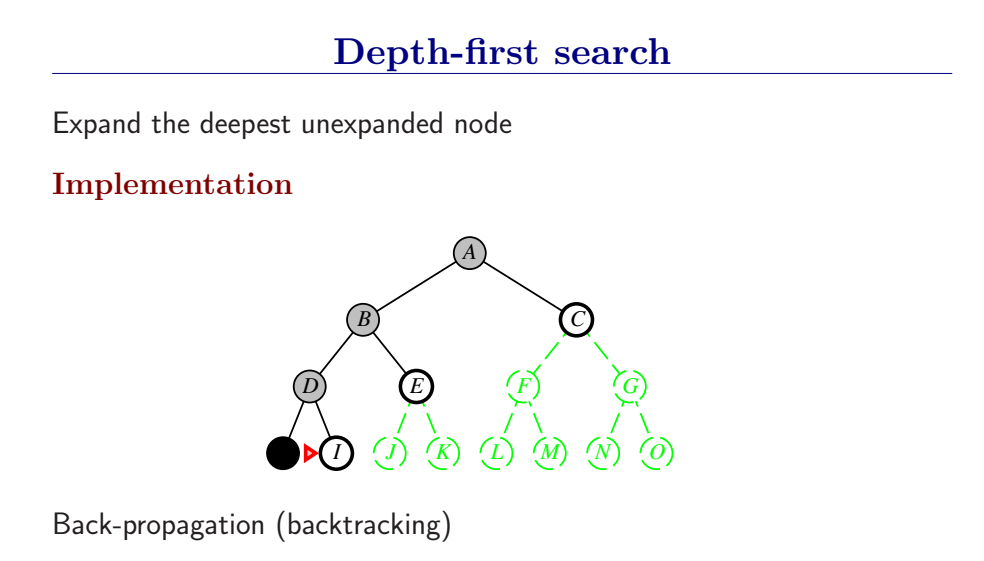
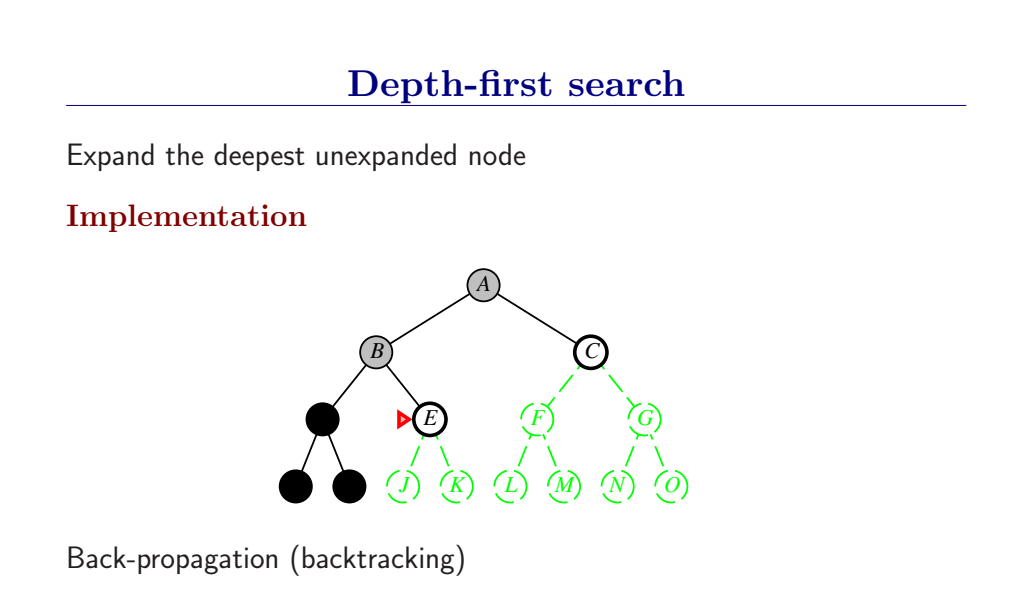
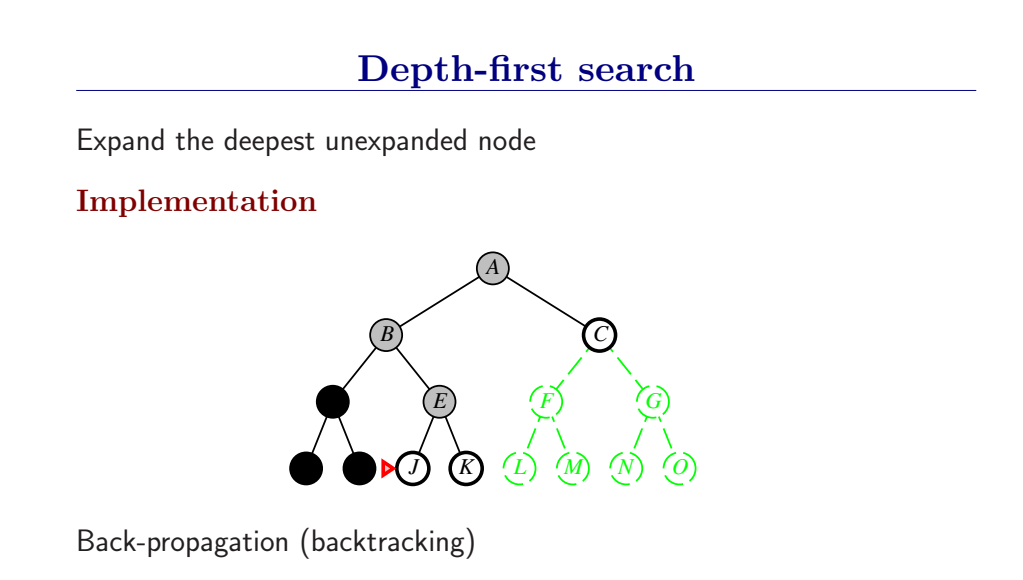
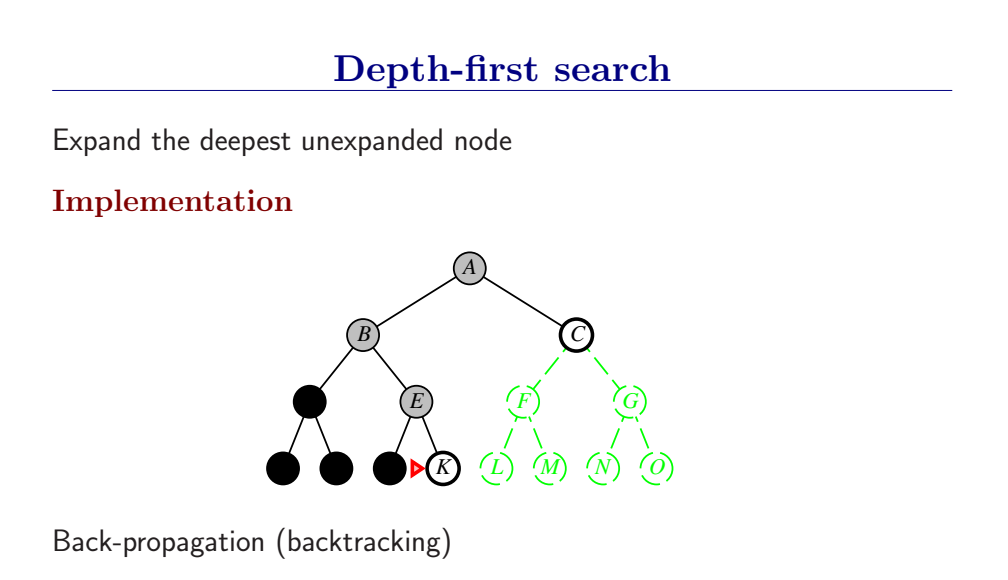
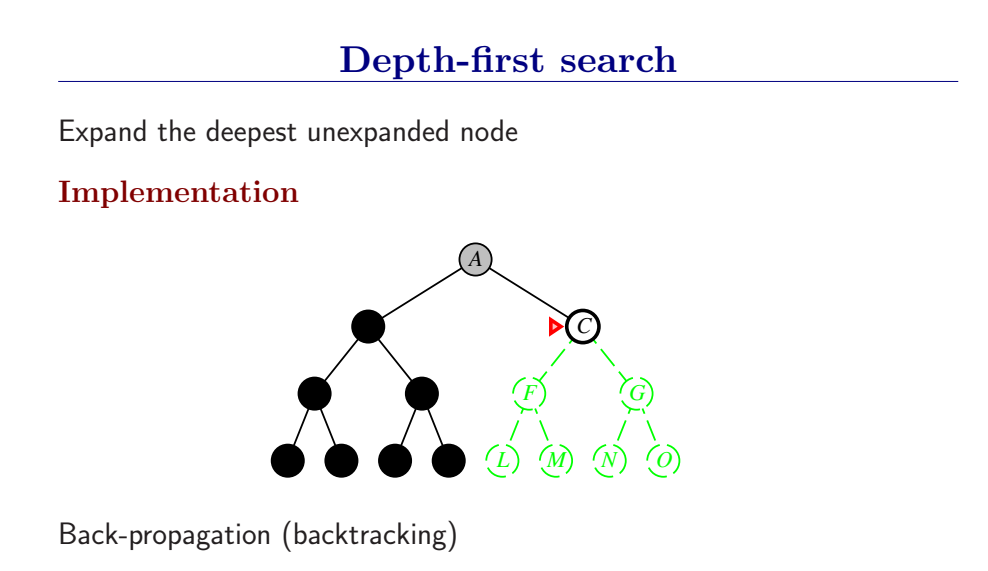
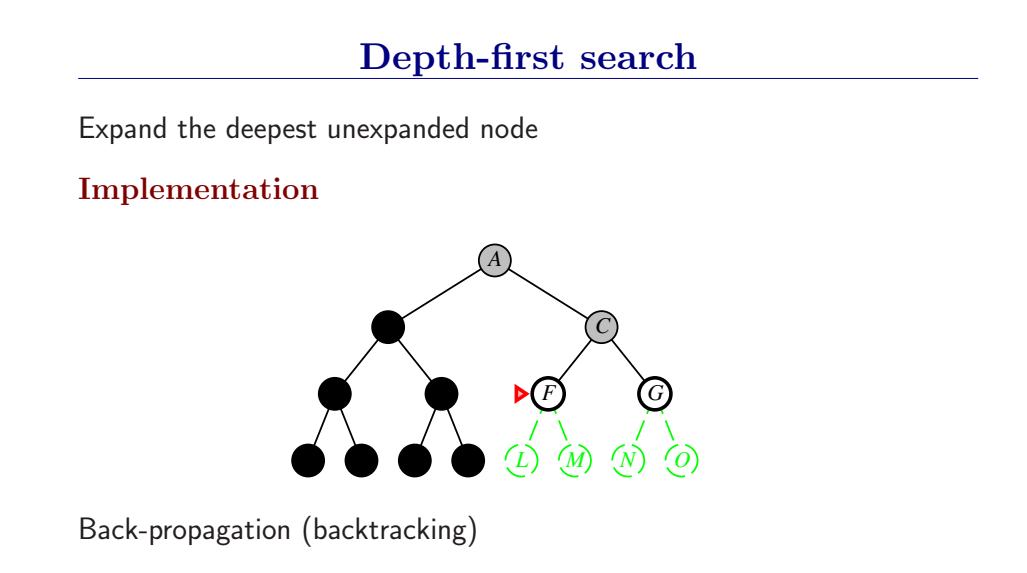
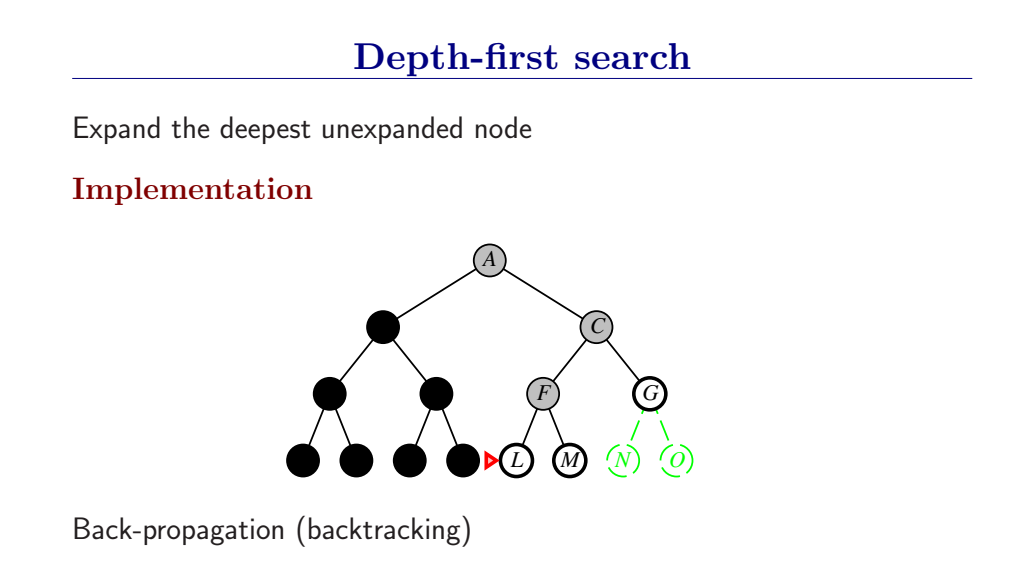
深度优先总是扩展搜索树的当前边缘节点集中最深的节点（搜索直接推到最深层）。如果最深层节点扩展完了，就回溯到下一个还有未扩展节点的深度稍浅的节点。

DFS使用LIFO队列（最新生成的节点最早被扩展），而且要调用自己的递归函数来实现DFS算法。（有深度界限的递归深度优先搜索算法）

DFS扩展根节点的一个后继，然后扩展它的一个后继，直到到达搜索树的最深层，那里的节点没有后继，于是DFS回溯到上一层，扩展另外一个未被扩展的节点。
在有限状态空间中，DFS是完备的，因为它可以把所有空间遍历一遍；而在无限空间中，DFS则有可能会进入深度无限的分支，因此是不完备的。
DFS的时间复杂度为为 $O(bd)$ ，而空间复杂度仅为 $O(d)$ ，因为我们只需要保存当前分支的状态，因此空间复杂度远远好于BFS。
然而DFS并不能保证找到最优解。

性能：
DFS的搜索效率严重依赖于使用的是图搜索还是树搜索。
如果是图搜索（避免了重复状态和冗余路径），那么DFS在有限状态空间就是完备的。
如果是树搜索，则不完备，因为会出现死循环（DFS算法本身是没有explored set的）。

因此性能不是最优的。

复杂度：时间复杂度受限于状态空间的规模，为： $O(b^m)$ ， $m$ 是任一节点的最大深度。这比 $d$ （最浅解的深度）要大的多。
但是空间复杂度很给力，为 $O(bm)$ 。所以DFS在AI的很多领域成为工作主力。

此外，还有一种变形叫做回溯搜索（backtracking search）：每次只产生一个后继而不是生成所有后继，每个被部分扩展的节点要记住下一个要生成的节点。这样，内存只需要O(m)而不是O(mb)。

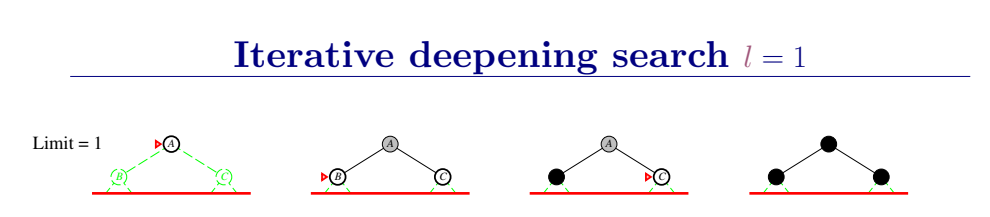
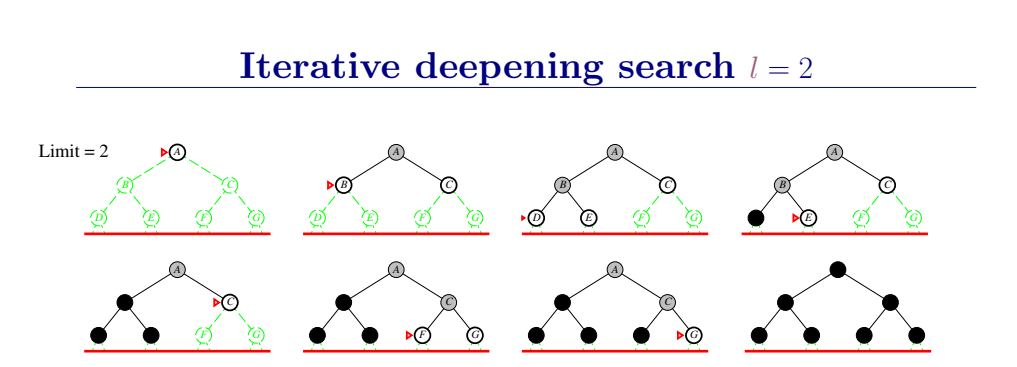
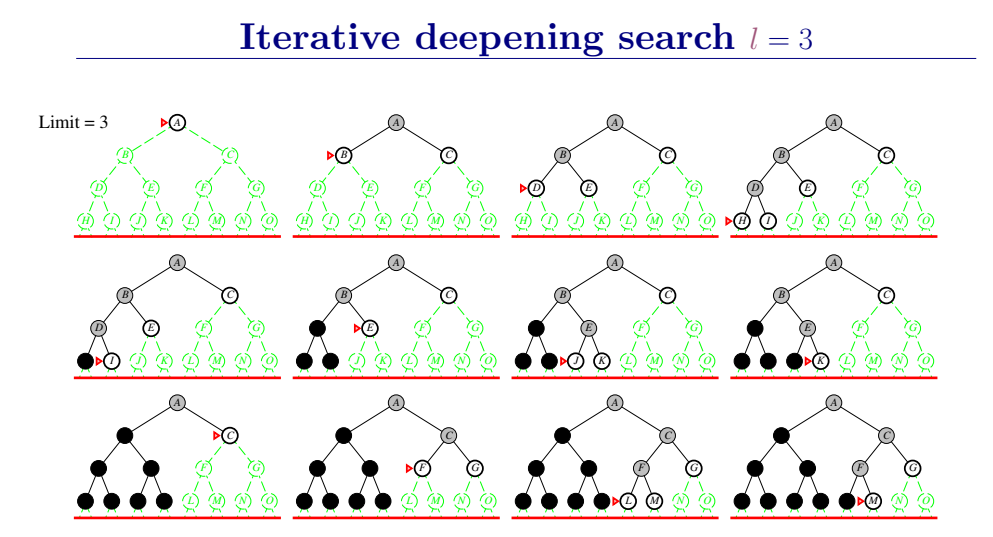
3.4.4 深度受限和迭代加深搜索

深度受限

设置界限I来避免DFS在无限状态空间下搜索失败的尴尬情况。
即，深度为I的节点被当做最深层节点（没有后继节点）来对待。

深度受限搜索设定一个最大深度dmax，当搜索深度大于dmax的时候立即回溯，从而避免了在无穷状态空间中陷入深度无限的分支。

迭代加深的深度优先算法 iterative deepening search（IDS）

为克服深度优先搜索陷入无穷分支死循环的问题，提出了有界深度优先搜索方法。有界深度搜索的基本思想是：预先设定搜索深度的界限，当搜索深度到达了深度界限而尚未出现目标节点时，就换一个分支进行搜索。

IDS = DFS + BFS。
可以说是结合了宽度优先和深度优先的优点：

1）空间复杂度：O(bd) （和DFS一样）；
2）在分支因子有限时完备，在路径待机时节点深度的非递减函数时最优（和BFS一样）。

迭代加深的深度有限搜索也设定一个最大深度dmax，开始我们把dmax设为1，然后进行深度受限搜索，如果么有找到答案，则让dmax加一，并再次进行深度有限搜索，以此类推直到找到目标。这样既可以避免陷入深度无限的分支，同时还可以找到深度最浅的目标解，从而在每一步代价一致的时候找到最优解，再加上其优越的空间复杂度，因此常常作为首选的无信息搜索策略。