图论基础

图论基础

1.什么是“图”

这里我们说的图特指图论中的图，图是描述于一组对象的结构，由节点和边组成

比如，这就是一张（无向）图：

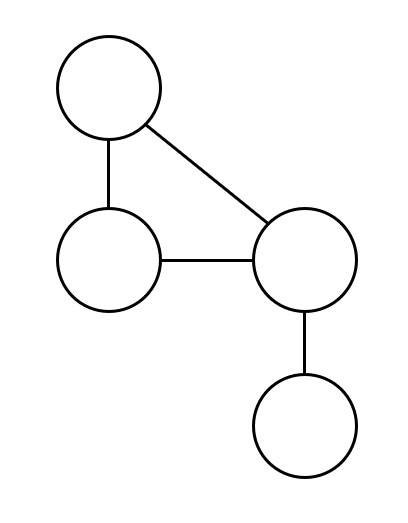
当然这其中还有很多分类

比如，有向图（同时它也是一个环）：

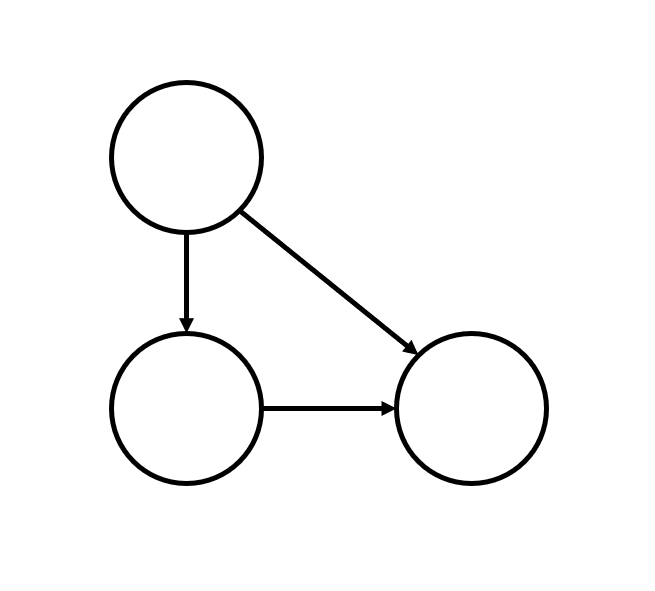
2.“树”

树是一种特殊的图，这是树的严谨定义：

　　任意两个顶点间有且只有一条路径的图

常用名词的定义：

　　1. 在树中有一个特定的节点被称为根节点，通常在最顶端

　　2. 一个节点含有的子树的根节点称为该节点的子节点

　　3. 从根开始定义起，根为第1层，根的子节点为第2层，以此类推

　　4. 树的高度或深度为树中节点的最大层

这就是一棵（高度为3的）树：

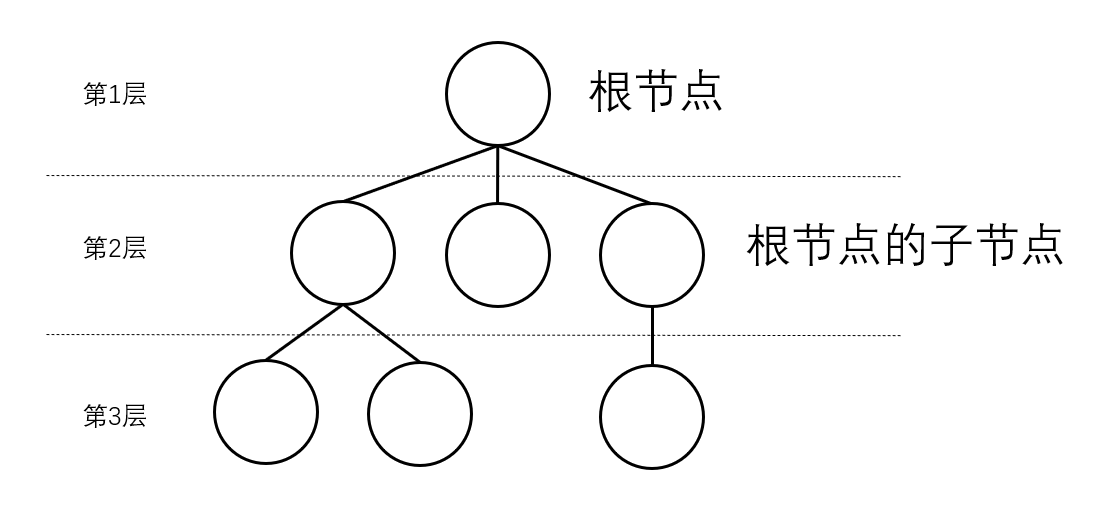
在一棵树中，若节点的个数为n，则边的个数为(n - 1)

特殊的，树中节点的度不大于2的有序树我们称其为二叉树

如：

 

 

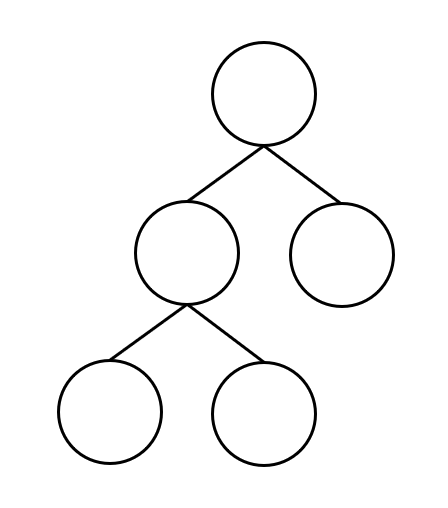
3.“树”的遍历

在实际程序中，若我们要遍历一棵树我们有一下几种选择

（为方便表示，我们为每一个节点标上序号）

 

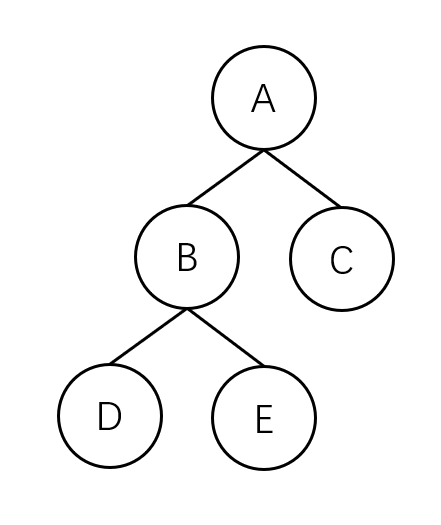
1. 前序遍历：首先访问根结点然后遍历左子树，最后遍历右子树

　　在遍历左、右子树时，仍然先访问根结点，然后遍历左子树，最后遍历右子树，如果二叉树为空则返回

　　以上我们习惯简称：根-左-右

　　这棵树的前序遍历为：A B D E C

2. 中序遍历：左-根-右（仅存在于二叉树）

　　这棵树的中序遍历为：D B E A C

3. 后序遍历：左-右-根

　　这棵树的后序遍历为：D E B C A

4.前/中/后缀表达式

在我们表示一个算式时常使用其中缀表达式，如：

　　a * ( b + c ) - d

但这样，在计算机处理时则需要麻烦地用到递归得到结果

于是，前缀表达式、后缀表达式出现了

我们首先可以把上面的表达式按其运算顺序放入一棵树中：

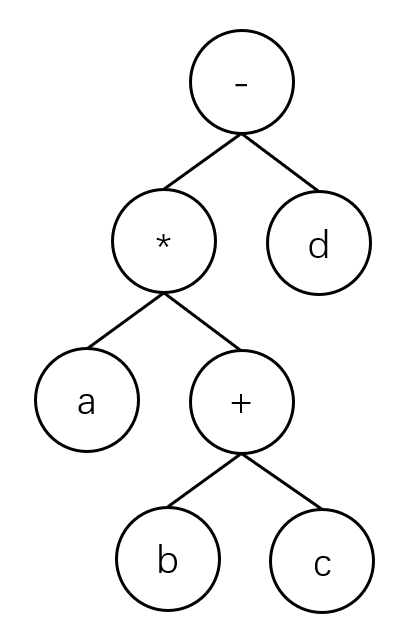
所谓的前/后缀表达式其实就是简单地将这棵树进行前/后序遍历

我们可以得到前缀表达式：- * a + b c d

后缀表达式：a b c + * d -