P6037 Ryoku 的探索

题目传送门

思路提供

首先，我们从题目中可以看到，存在 \(n\) 个点 \(n\) 条边，所以此题考查的是基环树，那么什么是基环树——

基环树是一个 \(n\) 个点 \(n\) 条边的图，比树多出现一个环。

因此，这棵树上是存在一个环的（而且很重要），所以我们要先找出这个环，基环树找环有两种基本的算法，一种是 DFS 而另一种就是我这次用的改编版的拓扑排序，即每次将连边数位 \(1\) 的点加入队列，再每次取出队头，遍历它所连的所有边，将它的所有连点的连边数都减去 \(1\) 再将连边数为 \(1\) 的点加入队列，如此往复，直到队列变空，由于环中的点都至少有两条连边，而且不会有点被加入队列，所以在循环结束后边数大于 \(1\) 的点就是环中的数。

//求环
void qh(){
	for(int i=1;i<=n;i++){
		if(lb[i]==1) q.push(i);
	}
	while(!q.empty()){
		int w=q.front();
		q.pop();
		for(int i=head[w];i!=0;i=edge[i].next){
			int xx=edge[i].to;
			lb[xx]--;
			if(lb[xx]==1) q.push(xx);
		}
	}
}

接下来，我们可以将这个环看作整个树的中心（即树的根节点），而每棵子树与环的连边只有一条，即这棵子树中的任意点的答案和它连接的环的点的答案是一样的，所以我们只要求出每个环中点的答案，再将其向各自的子树子树扩展就可以（可以利用 DFS ）

//为子树染色
void rs(int x){
	for(int i=head[x];i!=0;i=edge[i].next){
		int xx=edge[i].to;
		if(lb[xx]<=1 && !vis[xx]){
			ans[xx]=ans[x];
			vis[xx]=1;
			rs(xx);
		}
	}
}

最后最关键的就是求环中每个答案，我们可以先看一下题目中所给的样例的图——

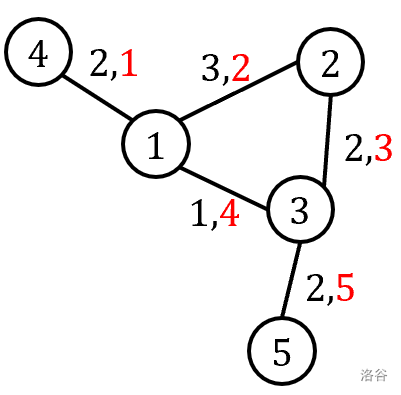
假如以 \(1\) 为出发点，它会先选取（\(1,4\)）这条边，再由 \(3\) 这个点进行扩展，而由于是 DFS 所以 \(3\) 会遍历完所以它连的边再回溯到 \(1\) ，即环中剩下的 \(2\) 也会被遍历到，所以 \(1\) 和 \(2\) 之间的连边就无效了（即不会被便利到）。

然后我们再以 \(3\) 为出发点，按照规律它会先选择 \(5\) 回溯后选择 \(1\) 而因为同上是 DFS 所以要遍历完 \(1\) 的所有可能才会回溯到 \(3\) 所以 \(2\) 会在 \(1\) 遍历所有连点的时候就被遍历过了，所以 \(3\) 和 \(2\) 之间的连边也无效了。

这样我们就可以发现一个规律——

环中的点与他在环中连接到两条边中美观值最小的边不会被遍历到，所以它的答案值就是总的长度减去那条不会被遍历到的边的长度（不理解可以根据样例再研究一下）。

//求环中点的答案值
void solve(){
	for(int i=1;i<=n;i++){
		if(lb[i]>1){
			int minn=1e9,flag;
			for(int j=head[i];j!=0;j=edge[j].next){
				int xx=edge[j].to;
				if(lb[xx]>1 && edge[j].beat<minn){
					minn=edge[j].beat;
					flag=edge[j].value;
				}
			}
			vis[i]=1;
			ans[i]=tot-flag;
			rs(i);
		}
	}
}

AC code

#include<bits/stdc++.h>
using namespace std;
#define int long long//一年 OI 一场空，不开 long long 见祖宗
const int N=1000005;
struct node{
	int to,next,value,beat;
}edge[N<<1];//前向星存边（记得双倍空间） 
int head[N],cnt,vis[N],ans[N],n,lb[N],tot;//tot记录总长度，vis表示有无被访问过，ans存储当前点的答案，lb表示当前点的连边数 
queue<int> q;//拓扑排序用的队列 
void add(int x,int y,int v,int b){
	cnt++;
	edge[cnt].to=y;
	edge[cnt].value=v;
	edge[cnt].beat=b;
	edge[cnt].next=head[x];
	head[x]=cnt;
}//前向星的加边函数 
//拓扑求环
void qh(){
	for(int i=1;i<=n;i++){
		if(lb[i]==1) q.push(i);
	}//将连边数为1的点（即叶子节点）加入队列 
	while(!q.empty()){
		int w=q.front();
		q.pop();//每次去出队头 
		for(int i=head[w];i!=0;i=edge[i].next){
			int xx=edge[i].to;
			lb[xx]--;
			if(lb[xx]==1) q.push(xx);//将符合要求的点加入队列 
		}
	}
}
//为子树染色
void rs(int x){
	for(int i=head[x];i!=0;i=edge[i].next){
		int xx=edge[i].to;
		if(lb[xx]<=1 && !vis[xx]){//必须是子树上的节点，要避免是环上的 
			ans[xx]=ans[x];
			vis[xx]=1;
			rs(xx);//继续向下遍历 
		}
	}
}
//求环中点的答案值
void solve(){
	for(int i=1;i<=n;i++){
		if(lb[i]>1){
			int minn=1e9,flag;//给minn赋值为极大 
			for(int j=head[i];j!=0;j=edge[j].next){
				int xx=edge[j].to;
				if(lb[xx]>1 && edge[j].beat<minn){
					minn=edge[j].beat;//求最小美观值 
					flag=edge[j].value;//求最小美观值边的长度 
				}
			}
			vis[i]=1;//DFS的准备 
			ans[i]=tot-flag;//先将环中点的答案值更新 
			rs(i);
		}
	}
}
signed main(){
	std::ios::sync_with_stdio(false);//可以是cin和cout的速度加快，不加会T一个点 
	cin>>n;
	for(int i=1;i<=n;i++){
		int x,y,p,b;
		cin>>x>>y>>p>>b;
		add(x,y,p,b),add(y,x,p,b);
		lb[x]++,lb[y]++;//将两个节点的连边数都加上1 
		tot+=p;//计算总值 
	}
	qh();
	solve();
	for(int i=1;i<=n;i++) cout<<ans[i]<<endl;//按顺序输出答案 
	return 0;
}