Stanford_CS224W----Message Passing and Node Classification

Stanford_CS224W----Message Passing and Node Classification

这节课针对上节课的传统方法不能利用节点特征的问题，提出了三个层层递进的Message Passing方法。
给定一个在某些节点上有标签的网络，我们如何给网络中所有其他节点分配标签？

三个层层递进的方法：

• Relational classification
• Iterative classification
• Belief propogation

Assumption:对于网络中节点的行为是相关的

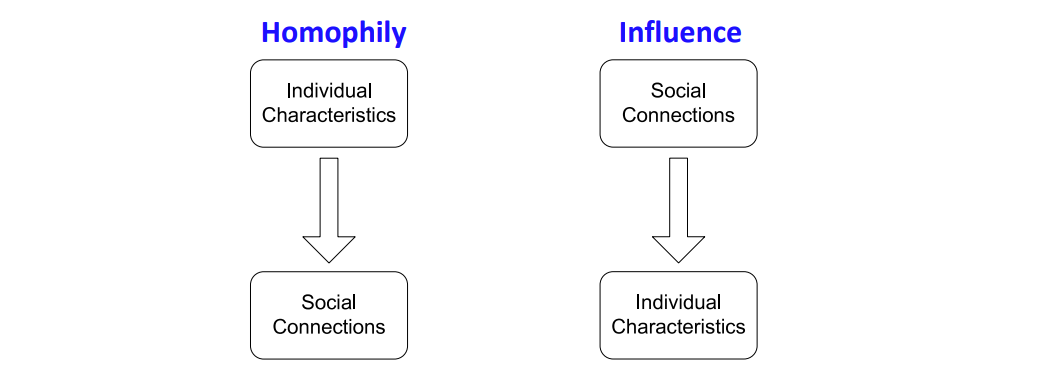
Relational classification

算法步骤:

1. 随机一个节点序列
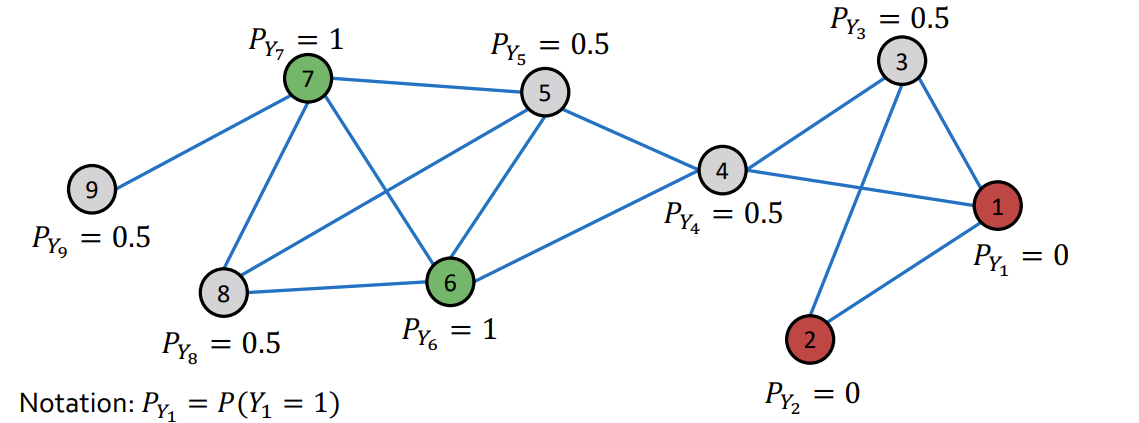
2. 对于所有已有标签的节点v，初始化一个值\(Y_v\)(值根据标签设置，比如绿为1，红为0)
3. 对于没有标签的节点，\(Y_v=0.5\)
4. 使用算法迭代更新节点值，直到收敛或者到达一定的迭代次数。

\[P(Y_v = c) = \frac{1}{\sum_{(v,u)\in E}A_{v,u}} \sum_{(v,u)\in E} A_{v,u}P(Y_u = c) \]

开头的分数是为了归一化

---

---

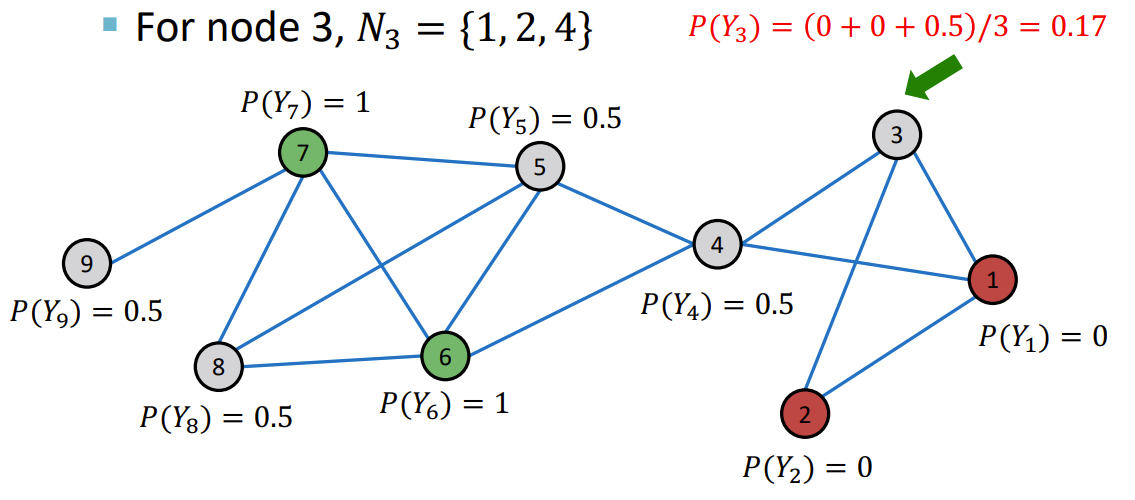
3，4，5，8，9 依次来

---

最后收敛

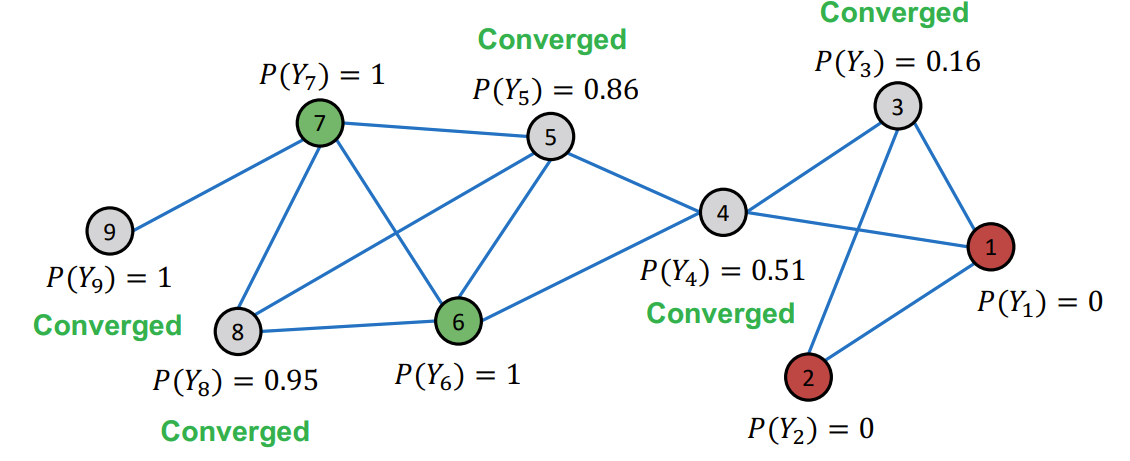
Challenges：

• 不能保证一定收敛
• 模型不能使用节点特征

Iterative Classification

Some definitions

输入:

• \(f_v\) : 节点\(v\)的特征向量
• 一些节点\(v\)被标签为\(Y_v\)

classifiers:

• \(\phi_1(f_v)\):基于节点的特征来预测节点的标签
• \(\phi_2(f_v，z_v)\)通过节点的特征和节点\(v\)的邻居的标签的信息\(z_v\)
  • \(z_v\)可以有以下定义
    • \(N_v\)中标签的数量总结信息
    • \(N_v\)中标签的众数
    • \(N_v\)中标签的种数

Steps

1. 利用已知标签节点训练分类器
2. 将分类器运用到测试节点上
3. 迭代直至聚合。(直接看例子比较明白)
   tpis：classifier是自己定的模型(线性模型之类的)

---

训练\(\phi_1\)分类器

---

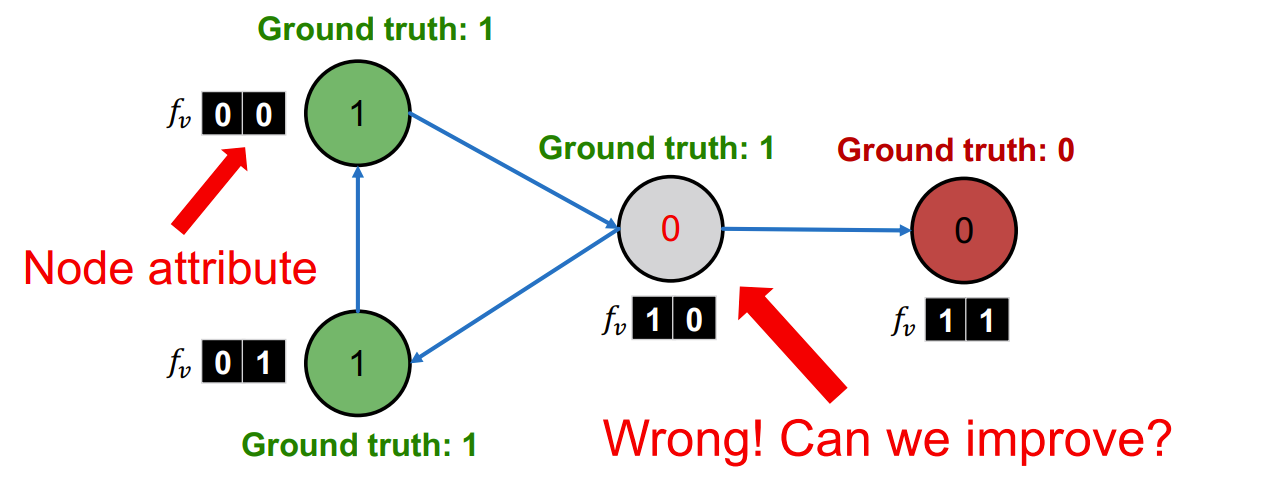
• \(I\) = Incoming neighbor label information vector.
• \(O\)= Outgoing neighbor label information vector.
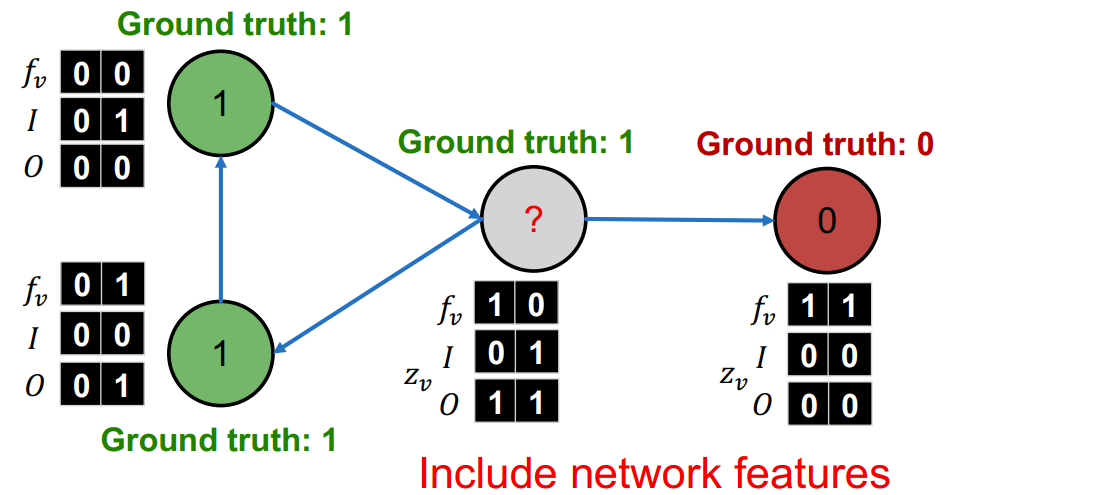
  • \(I_0\) = 1:如果连入的网页至少有一个为label 0. Similar definitions for \(I_1\), \(O_0\), and \(O_1\)
    

---

通过分类器，再迭代更新\(f_v\)和\(z_v\)即可

C&S or Belief propogation

有机会可以看看C&S