Stanford_CS224W----Node Embeddings

Stanford_CS224W----Node Embeddings

对图的节点和图本身进行嵌入处理。

传统的机器学习步骤，过程简单总结就是特征提取+学习算法

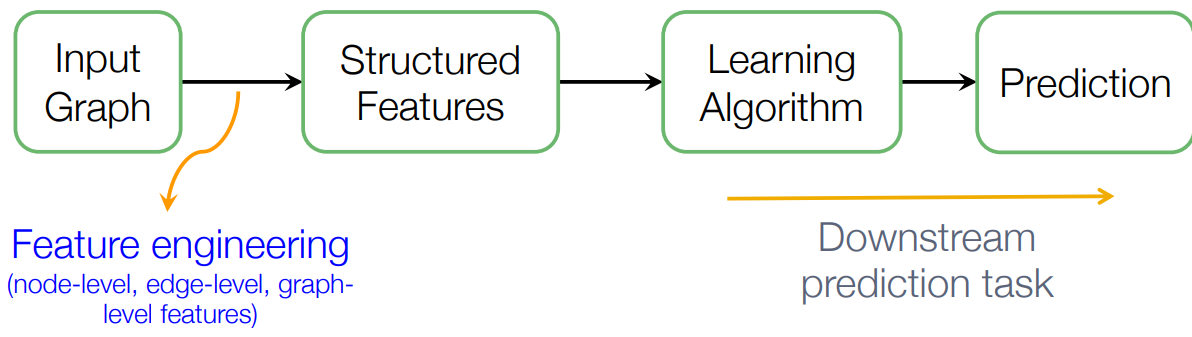
而图表征学习则将特征提取进行自动化。

Goal：获得高效的任务无关的特征，并且用于机器学习

这节课将的就是将节点嵌入向量空间。为了简单演示，选择优化一个look-up

为什么选择将节点嵌入

• 节点之间嵌入的相似性表明网络中的节点相似性
• 编码了网络信息
• 有可能用于许多下游的预测

Encoder & Decoder

定义$u$和$v$在向量空间映射为$z_u^T$和$z_u$

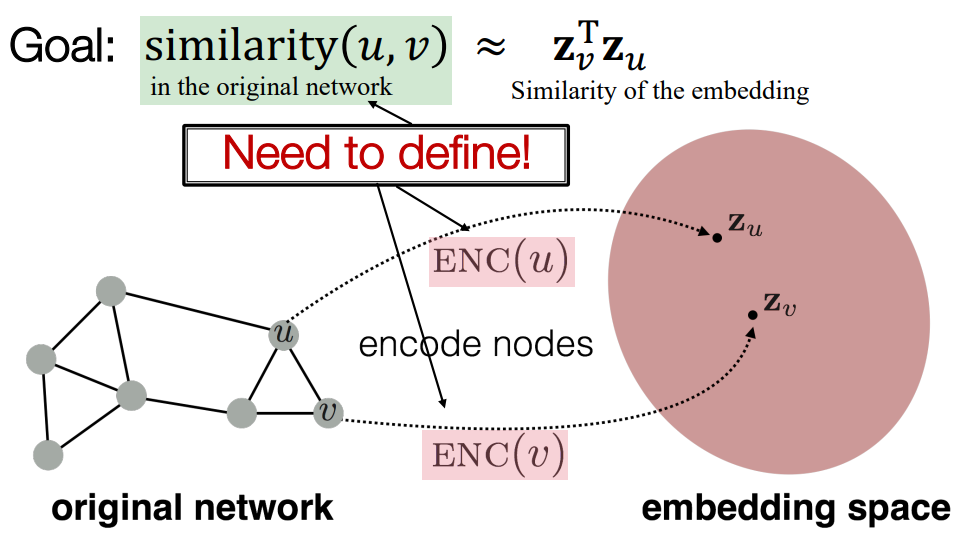
可以看到，需要定义两个组件，一个是相似性（关系到选择的算法），一个是编码器（这里选择最简单的look-up）其他的decoder，取决于节点相似性$z_v^T{z}_u$。
优化目标（Objective）：对于相似的节点对$（u,v）$最大化$z_v^T{z}_u$

Random Walk Approaches for Node Embeddings

给定一个图和一个起点，我们随机选择它的一个邻居，并移动到这个邻居；然后我们随机选择这个点的一个邻居，并移动到它，等等。 以这种方式访问的点的（随机）序列是图上的随机行走。

$$z_u^T{z}_v\approx probabilitythatuandvco-occuronarandomwalkoverthegraph$$

如果从u走到v具有很高的可能性，那么u和v是相似的

Expressivity：节点相似性的可变化的随机定义，包含了本地和高阶邻域信息。

Efficiency：每次只考虑在随机路上的一同出现的节点对

Random Walk Strategy

不同的游走策略定义了不同的$N_R(u)$，但其他计算内容是相似的，优化使用随机梯度下降

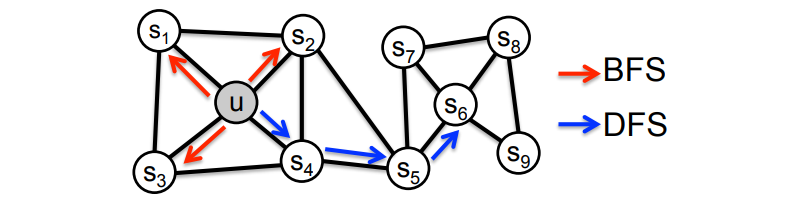
上图为biase-walk，一般有俩个参数

• p: 返回上一步的概率
• q: 选择DFS和BFS的比例概率

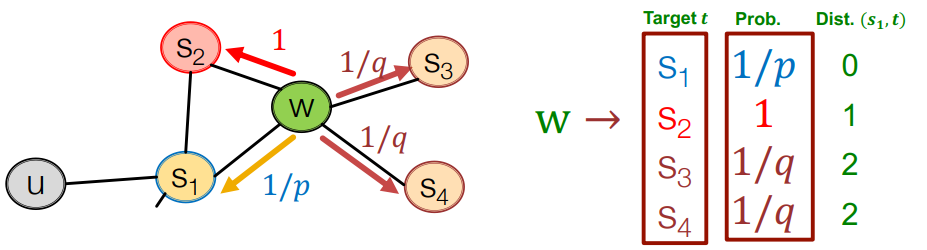
• 其他的随机游走ideas

  • Based on node attributes (Dong et al., 2017)
  • Based on learned weights (Abu-El-Haija et al., 2017)

• 可选的优化方法

  • Directly optimize based on 1-hop and 2-hop random walk probabilities (as in LINE from Tang et al. 2015)

• 网络处理技术

  • Run random walks on modified versions of the original network (e.g., Ribeiro et al.2017’s struct2vec, Chen et al. 2016’s HARP).

Optimization

我们的目标是学习一个映射：$f:u\to {ℝ}^d:f(u)=z^u$

对数似然优化目标

$$ma{x}_f\sum _{u\in V}logP(N_R(u)|z_u)=\sum _{u\in V}\sum _{v\in N_R(u)}logP(v|z_u)$$

其中$N_R(u)$是在游走策略中定义的附近的点。

同时对P进行定量化，这里使用了$softmax$函数，我们希望节点v是与节点u最相似。

$$P(v|z_u)=\frac{\exp (z_u^T{z}_v)}{\sum _{n\in V}\exp (z_u^T{z}_n)}$$

但是这个计算复杂度是$V^2$的

解决方法负采样：在所有点中选取概率和度成比例的部分点（关于数量：1. 较高的数量对应于对负面事件的较高偏向性 2. 较高的数量能提供更可靠的估计）一般取$k=5-20$

同时有

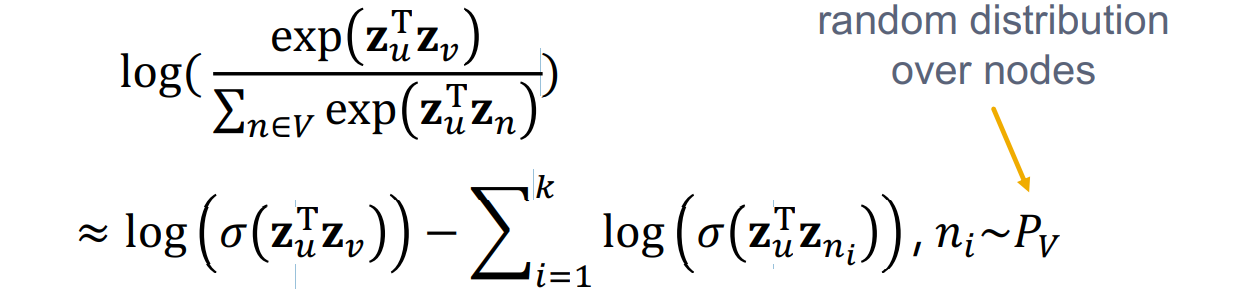
a litile summary

node2vec在节点分类方面做得比较好，同时也更高效。记得选择符合应用的相似性定义。

Embedding Entire Graphs

Goal：将整个图映射到向量空间中

这里讲了三种方法

Simple idea 1

直接通过上文所述的方法，对每个节点进行嵌入。最后对所有节点进行处理（求和或者平均）

$$z_G=\sum _{v\in G}{z}_v$$

Used by Duvenaud et al., 2016 to classify molecules based on their graph structure

idea 2

引入了一个“虚拟点”的概念，对虚拟点进行游走算法，得到的向量则为虚拟点连接的图（子图）的图向量。

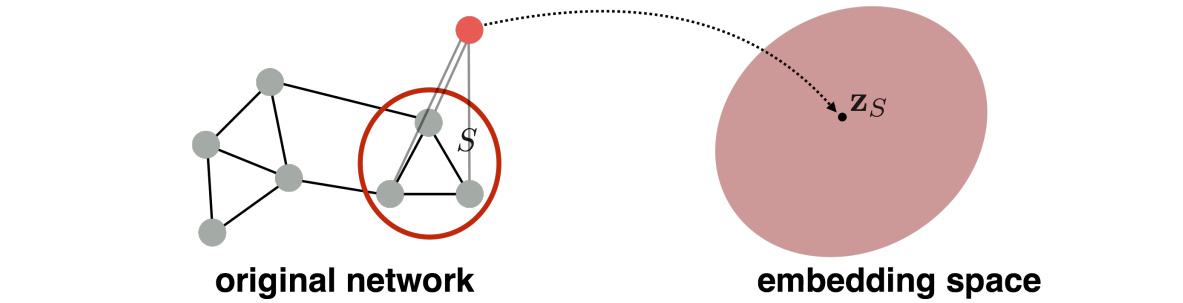
Proposed by Li et al., 2016 as a general technique for subgraph embedding

Anonymous Walk Embeddings

Anonymous的意思是，游走的结果中和节点无关，纯纯代表了图的结构。

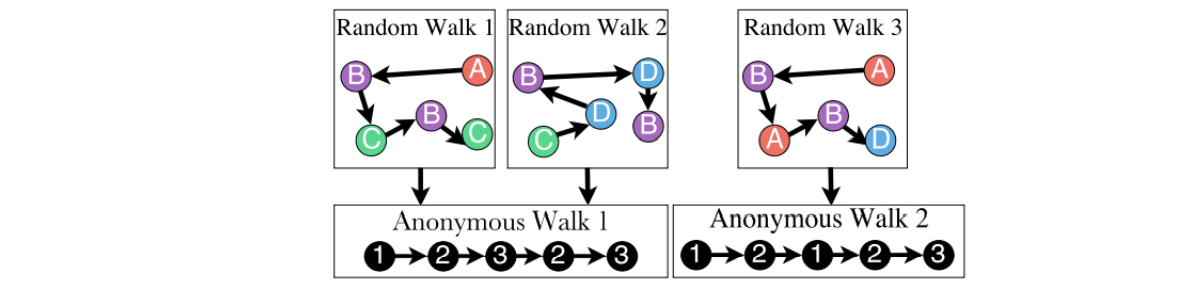
每次游走能得到一个walk序列，之后对所有的walk序列进行处理，则能得到图的图嵌入向量$z_G$。类似处理为word2vec了

aproach 1

统计每个游走出现的次数，最后将每种游走归一化，将最后的概率向量作为图向量$z_G$。
比如：

1. l=3, 长度为3，得到5种匿名游走。111，112，121，122，123
2. $z_G[i]$= probability of anonymous walk $w_i$ in $G￥

将频数表示为概率，需要大量的实验才能证明频率和实际频率相差无一

有一个公式可以预计出需要游走的步数m。m可以使得误差不大于$ϵ$,不小于$\delta$，其中$\eta$为长度l的匿名随机游走数

$$m=[\frac{2}{{ϵ}^2}(log(2^{\eta }-2)-\log (\delta ))]$$

aproach 2

对匿名游走进行嵌入，最后得到一个向量矩阵作为图的向量嵌入。计算方法类似于word2vec的skip-gram，不再赘述。

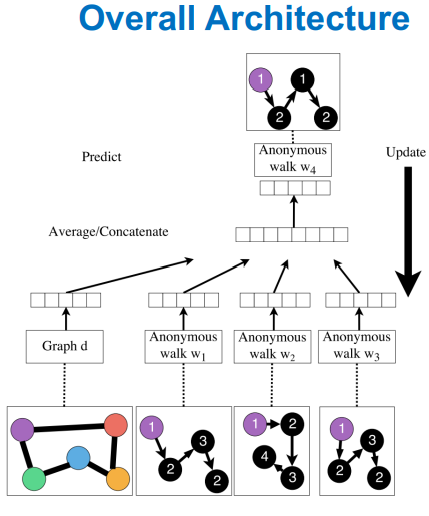
summary

最后总结一些可以利用node embedding的方法

• Clustering/community detection: Cluster points $z_i$
• Node classification: Predict label of node $i$ based on z_i
• Link prediction: Predict edge $(i,j)$ based on $(z_i,z_j)$
  • Concatenate: $f(z_i,z_j)=g([z_i,z_j])$
  • Hadamard: $f(z_i,z_j)=g(z_i\ast z_j)$ (per coordinate product)
  • Sum/Avg: $f(z_i,z_j)=g(z_i+z_j)$
  • Distance: $f(z_i,z_j)=g(||z_i,z_j|{|}_2)$
• Graph classification: graph embedding z_G via aggregating node embeddings or anonymous random walks. Predict label based on graph embedding z_G