shu-jia
暑假
NOIP2023模拟测试赛(一)
A
每个数出现 \(\ge2\) 次,可以容斥:
钦定 \(0\) 个数出现 \(<2\) 次,减去钦定 \(1\) 个数出现 \(<2\) 次,加上钦定 \(2\) 个数出现 \(<2\) 次,...
钦定 \(i\) 个数出现 \(<2\) 次怎么算?假设它们是前 \(i\) 个数(最后乘上 \(\binom n i\))。
如果是全出现一次,则可以把这 \(i\) 个数划分成若干集合,每个数都被划分且每个集合都有数。
这个方案数就是斯特林数 \(i\brace j\),\(j\) 是枚举的集合数量。
如果允许有出现 \(0\) 次的,那这些 \(0\) 次的数再放进一个集合。注意这个集合可能没有数,不符合斯特林数的定义,
那就再假设有一个数,提前给它放到这个集合中。方案数就是 \({i+1}\brace{j+1}\)。
我们还需要考虑剩下 \(n-i\) 个数。这些数在已经选好的 \(j\) 个集合中可以任意出现,
有 \((n-i)j\) 个位置,每个位置可以选择出现或者不出现,方案数即 \(2^{(n-i)j}\)。
除此之外,还有一些集合可以被选择,那就是不选前 \(i\) 个数的集合(前 \(i\) 位均为 \(0\))。
这些集合无所谓选不选,对前 \(i\) 位无影响。它们的选择方案数是 \(2^{2^{n-i}}\)。最后答案为
直接计算,复杂度 \(\mathcal O(n^2)\)。
B
先假设全树选择次数均为某个数 \(k\)。我们每次可以选择一棵非全树的子树 \(u\),把这棵子树选择次数加 \(1\)。
那么会导致答案加了 \(siz_u\),总重量加了 \(\sum_{v\in t_u} m_v\)。
现在变成这么个问题:\(n\) 个物品,\(\sum m\) 作为体积,\(siz_u\) 作为价值,物品 \(1\) 有无限个,其他物品有 \(d\) 个,求体积上限内最大能得到的价值和。
这是一个多重背包,可以二进制分组解决。可是 \(d\) 太大,过不去。
考虑一个错误贪心:把所有物品按性价比 \(\frac w v\) 从大到小排序,从大到小能选就选。
这个贪心什么时候正确?若 \(\frac{w_i}{v_i}>\frac{w_j}{v_j}\),我们可以把 \(w_i\) 个物品 \(j\) 替换成 \(w_j\) 个物品 \(i\),因为它们的价值均为 \(w_iw_j\),但前者体积为 \(w_iv_j\),大于后者体积 \(w_jv_i\)。
这意味着排完序如果性价比偏低的 \(j\) 个数大于性价比偏高的 \(i\) 的 \(w_i\),且 \(i\) 还能放(个数少),可以把 \(j\) 替换掉。
注意到 \(w_i=siz_i\le50\)。所以说,大范围里我们可以贪心,小范围用背包解决即可。
具体地,每个物品拿 \(\min(50,d)\) 个出来多重背包,之后枚举每一种权值对应的最小体积,剩余体积贪心分配。
这里由于体积大,权值小,背包的状态要换一下,不再是一定体积能装的最大权值,而是一定权值需要的最小体积。
复杂度 \(\mathcal O(n^4\log n)\)。
C
根据幻想乡战略游戏的经验,权值由一个点从小到大向外发散。
什么,你问我证明??听说是凸函数相加仍为凸函数,我不太懂!!
还是套路点分,但不同于 P3345,这里 dis 带了个 \(1.5\) 的指数,不能直接点分树维护。
也不能每次爆搜 \(v\),万一度数很大就完蛋了。
于是使出所谓的凸函数的神秘方法,假设答案不在点上而在边上,考察只有两个点的情况:
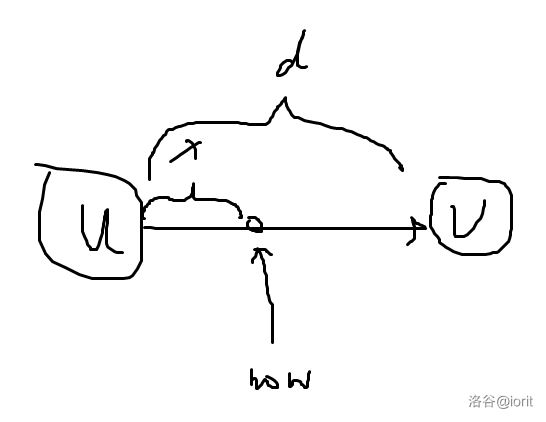
\(weight=f(x)=\sum_{w\in t_v}(dis(w,u)-x)^{1.5}a_w+\sum_{w\not\in t_v}(dis(w,u)+x)^{1.5}a_w\)
这是一个关于 \(x\) 的下凸函数,它可能有以下三种姿态:
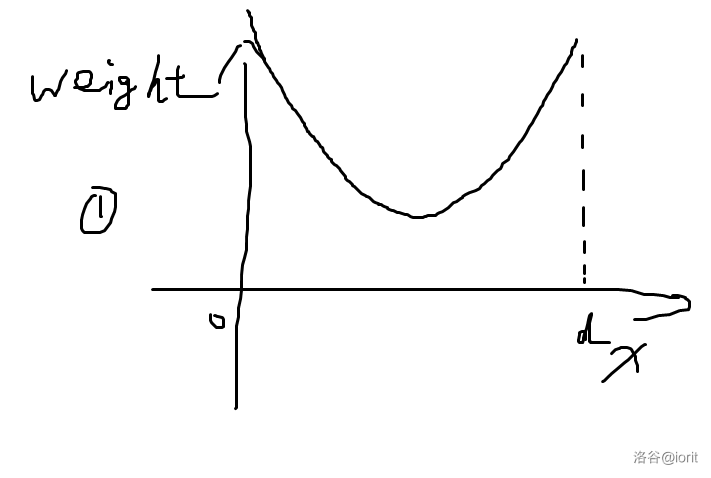
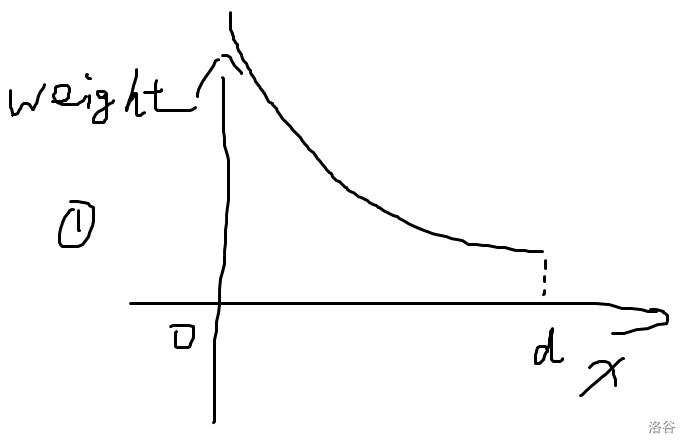
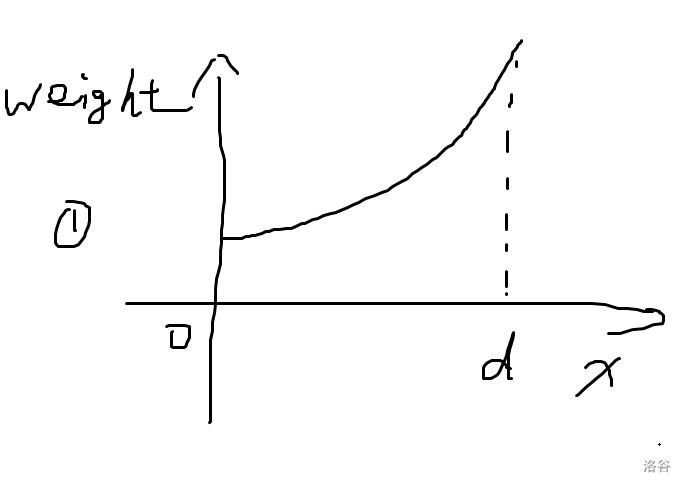
第一种,说明最优点在边上。那么 \(u,v\) 两点中有一者是答案。
第二种,说明从 \(u\) 走到 \(v\) 答案不断减小。那么就往 \(v\) 走吧。
第三种,说明从 \(u\) 走到 \(v\) 答案不断增大。那么不应该往 \(v\) 走,考虑其他儿子吧。
我们发现,\(f'(0)\) 的正负性可以判断出要不要走到 \(v\)(不管第一种,我们实时更新答案即可。)
这个可以从 \(u\) 出发,一次 dfs 预处理得到。于是就不用 dfs 每个 \(v\) 了,解决了最大的问题。
复杂度 \(\mathcal O(n\log n)\)。
NOIP2023模拟测试赛(二)
A
先求出最小生成树,记它的权值为 \(M\)。分类讨论:
-
若 \(X<M\),显然怎么染权值都不可能小于最小的权值,答案为 \(0\)。
-
若 \(X=M\),随便搞出一个最小生成树,设为 \(T\)。
考虑最小生成树的通用处理,对每条树外边 \(E\),求出它两个端点在 \(T\) 上之间的边权最大值。
设最大值减去边权的值为 \(d_E\),显然 \(d_E>=0\),否则就不是最小生成树了。
如果我们把当前的树染成同色的(设为黑),那我们要保证其它最小生成树中有异色的。
其他的最小生成树一定是由一些 \(d_E=0\) 的边替换掉一些当前树的边得到的。设这些边数量为 \(c_0\),
则这 \(c_0\) 条边中一定有至少一条白色的。其他边怎么染都无所谓,不会出现在最小生成树中。
方案数即 \(2\times(2^{c_0}-1)\times(2^{m-(n-1)-c_0})\)。(2 表示树是黑还是白)
如果我们把当前的树染成异色的,那已经满足条件,剩下边随便怎么染都行。方案数即 \((2^{n=1}-2)\times2^{m-(n-1)}\)。
- 若 \(X>M\),还是搞出一个生成树,求出 \(d_E\)。
由于 \(X>M\),这棵生成树只能染同色,设为黑色。树外边会分成三类:
1.\(d_E<X-M\)。这些边如果替换进来,生成树权值还是小于 \(X\),因此它们必须全部染成黑色。
注意这里不存在替换两条的情况。替换两条的权值大于替换一条,如果替换两条可行,其中至少有一条白色的,如果直接替换这一条,生成树权值应该小于 \(X\),不符合题意。
2.\(d_E=X-M\)。这些边替换进来刚好权值是 \(X\),它们之中应该至少有一条白色的。
3.\(d_E>X-M\)。这些边替换进来不影响答案,随便怎么染都行。
设 \(c_2\) 表示第二类边数量,\(c_3\) 表示第三类边数量,方案数即为 \(2\times(2^{c_2}-1)\times2^{c_3}\)。
B
\(1\) 在哪个位置都一样,不妨设他在第一位,最后答案乘上 \(2^n\)。
现在简单来说,\(1\) 想赢,要满足 \(\min\{p_2\},\min\{p_3,p_4\},\min\{p_5,p_6,p_7,p_8\}\dots,\min\{p_{2^{n-1}+1},\dots,p_{2^n-1},p_{2^n}\}\) 这些数中没有出现 \(a\) 中的数。
考虑容斥,设上述分组完的 min 分别为 \(mn_1,mn_2,\dots,mn_n\)。求出 \(f(S)\) 表示 \(S\) 中包含的 \(mn\) 全都在 \(A\) 中的方案数(\(S\) 是由若干 \(mn\) 组成的集合。)
答案即为 \(\sum_S(-1)^{|S|}f(S)\)。如何求出 \(f(S)\)?考虑 dp,设 \(dp_{i,S}\) 表示只考虑前 \(i\) 大的 \(a\) 时的 \(f(S)\)。
转移:每多一个更小的 \(a_i\),我们可以继承之前的状态,即 \(dp_{i,S}\gets dp_{i-1,S}\)。
也可以考虑新开一个集合,令其中最小值为 \(a_i\)。即
这里枚举了新的集合 \(j\),乘 \(2^{j-1}\) 是因为第 \(j\) 个集合大小就是 \(2^{j-1}\),\(a_i\) 放哪里都可以;
乘 \(A_{2^n-a_i-\sum_{x\in S}|x|}^{2^{j-1}-1}\) 是考虑剩下 \(2^{j-1}-1\) 个位置放的数,这些位置只要放大于 \(a_i\) 的数即可。
可选的数的数量为 \(2^n-a_i-\sum_{x\in S}|x|\),还要减去 \(\sum_{x\in S}|x|\) 的原因是要减去之前在 \(S\) 中已经放过的数的数量。
由于 \(a\) 从大到小转移,这些数一定全部大于 \(a_i\)。所以不会算重也不会算漏。
实现时,\(\sum_{x\in S}|x|\) 就是枚举二进制数时的 \(S\)。复杂度大概 \(\mathcal O(nm\log n)\)。
C
考虑 dp。设 \(dp_i\) 表示前 \(i\) 位划分的方案数。
转移考虑枚举最后一段的左端点,如果这一段出现一次的数数量 \(\le k\) 则可以转移。
这样是平方的。考虑数据结构优化,转移到 \(i\) 时维护数组 \(b\),\(b_j(j\le i)\) 表示 \([j,i]\) 出现一次的数数量。
向右移动一格到 \(i+1\) 时,设 \(a_i=x\),则将 \((pre_x,i+1]\) 的 \(b\) 加 \(1\),\((pre2_x,pre_x]\) 的 \(b\) 减 \(1\)。
这里 \(pre_x\) 表示上一个 \(x\) 的位置,\(pre2_x\) 表示上上个 \(x\) 的位置。
现在问题变成,区间 \(b\) 加减 \(1\),求 \(b_j\le k\) 位置的 \(dp_{j-1}\) 的和。
考虑分块,虽然教主的魔法只能根号log,但这题有特殊性质:每次加减的数为 \(1\),且每次都是查询 \(k\)。
考虑每块内维护桶,修改时整块打上标记,因为只加减 \(1\),答案可以根据桶 \(\mathcal O(1)\) 维护。
散块直接重构,重构时也可以顺便维护答案。这样就做到了一个根号。
复杂度 \(\mathcal O(n\sqrt n)\)。
NOIP2023模拟测试赛(三)
A
一个括号序列合法,当且仅当我们把 ( 设成 \(1\),) 设成 \(-1\),满足设出来的序列所有前缀和 \(\ge0\) 且总的和为 \(0\)。
这里,我们建出 SAM。为了在 SAM 上方便处理,把上述检验中所有前缀变成后缀,\(1\) 和 \(-1\) 交换一下。
SAM 中每个节点表示了一些本质相同的字符串。维护每个节点 \(\text{endpos}\) 中任意一个结束位置 \(x\)。
设这个节点代表的子串的左端点区间为 \([l,r]\)。固定子串的右端点,左端点越向左,越难以满足“所有后缀和 \(\ge0\)”的条件。
我们可以用 st 表 / 线段树二分等数据结构,或者单调栈,对数时间或均摊 \(\mathcal O(1)\) 的复杂度内二分出这个临界点 \(k\)。对于右端点在 \(x\) 的子串,若它的左端点小于等于 \(k\),则这个子串一定不合法。
如果 \(k>r\),那么这个节点代表的子串都是不合法的。否则令 \(k=\max(k,l)\)。
现在要求的是,右端点在 \(x\),左端点在 \([x,r]\) 的所有子串中有多少个和为 \(0\)。(赋值完 \(1\),\(-1\) 之后)
设序列的前缀和数组为 \(pre\)。也就是求 \([x-1,r-1]\) 内有多少个 \(i\) 满足 \(pre_i=pre_x\)。
随便搞,扫描线可以做到线性。
最后复杂度线性对数,或者精细的话线性。
B
C
神题
环上不会有相邻的两个 \(\ge \lceil\frac{m}2\rceil\) 的数。假设 \(\ge \lceil\frac{m}2\rceil\) 的数称作大数,否则称为小数。
那么整个环的构成有两种可能:

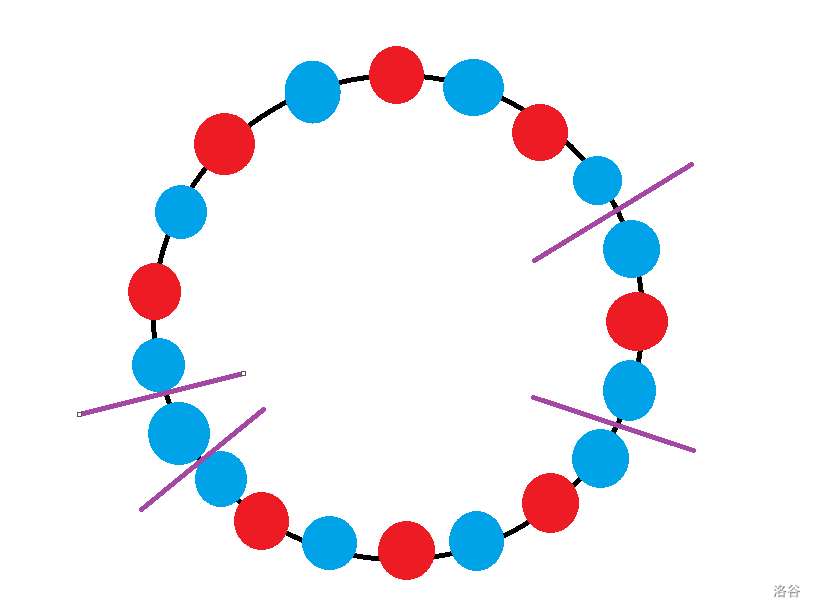
如上,红色代表大数,蓝色代表小数。
第一种情况下,整个环大小数交替。
第二种,整个环可以从每两个小数之间断开,变成若干链。
我们先研究第二种如何计算。设 \(a_{m,n}\) 表示长度为 \(n\) 的序列,在 \(m\) 下大小数交替,以小数开头小数结尾的方案数。
求出序列 \(a_m\) 的 OGF \(A_m\),则把这些链拼成长度为 \(n\) 的链的方案数即
设 \(W=\frac1{1-A_m}\),\(W\) 各项系数为 \(w\)。这里拼的是环,我们要拼的是链。考虑断环为链,如果:
-
\(1,n\) 之间的断点没有链覆盖,则方案为 \(w_n\)。
-
否则有一条链跨越 \(1,n\) 之间,枚举它的长度 \(i\),则方案为 \(\sum_i(i-1)a_iw_{n-i}\)。(断点有 \(i-1\) 种可能,这条跨越的链有 \(a_i\) 种可能,剩下是长为 \(n-i\) 的链)
下面来求 \(a_m\)。有一个很神的转化,把 \(a\) 中大数全部减去 \(\lceil\frac m2\rceil\),剩下的相邻两项之和小于 \(\lfloor\frac m2\rfloor\)。
而且这两种方案一一对应(可以想象一下)。
设 \(f_{m,n}\) 表示长度为 \(n\) 的序列,相邻两项之和小于 \(m\) 的方案数(原问题去掉环。)
那么因为一一对应,有 \(a_{m,i}=f_{\lfloor\frac m2\rfloor,i}\)(\(m-\lceil\frac m2\rceil=\lfloor\frac m2\rfloor\))。
现在让我们求 \(f\)。像环一样,考虑把序列从两个小数之间断开。与环不同,头尾两段的序列不一定要小数开头小数结尾,而开头一段可以大数开头小数结尾,结尾一段可以小数开头大数结尾。
考虑设 \(b_{m,n}\) 表示长度为 \(n\) 的序列,在 \(m\) 下大小数交替,以大数开头小数结尾的方案数(可以为空)。
大数开头小数结尾的方案显然是一样的。设 \(B_m\) 为 \(b_m\) 的 OGF,则答案的 OGF 为 \(\frac{B^2}{1-A}\)。
这里漏掉了一种情况,和环一样可能只有大小数交替没有可以断开的地方,且大数开头大数结尾。
我们令小数加上 \(\lceil\frac m2\rceil\),大数减去 \(\lceil\frac m2\rceil\),则这就变成了先前 \(a\) 定义的方案(小数开头小数结尾,大小数交替)。
于是答案的 OGF 应该是 \(\frac{B^2}{1-A}+A\)。
剩下还有环的第一种情况,即整个环大小数交替。还是将大数减去 \(\lceil\frac m2\rceil\),这变成一个 \(m\gets \lfloor\frac m2\rfloor\) 的原问题。
递归解决即可。这里将 \(\lfloor\frac m2\rfloor\) 的子问题还原回原问题有 \(2\) 种方式,奇数位加 \(\lceil\frac m2\rceil\) 或者偶数位加 \(\lceil\frac m2\rceil\)。
每层做一个求逆,共有 \(\log m\) 层,复杂度 \(\mathcal O(n\log n\log m)\)。
NOIP2023模拟测试赛(四)
A
在每个数出现次数不变的规则下,所有序列都可以转化为以下两种序列之一:
-
\(\{1,2,1,2,1,2,3,2,3,4,3,4,\dots,x-1,x,x-1,x\}\)
-
\(\{1,2,1,2,1,2,3,2,3,4,3,4,\dots,x-1,x,x-1,x,x-1\}\)
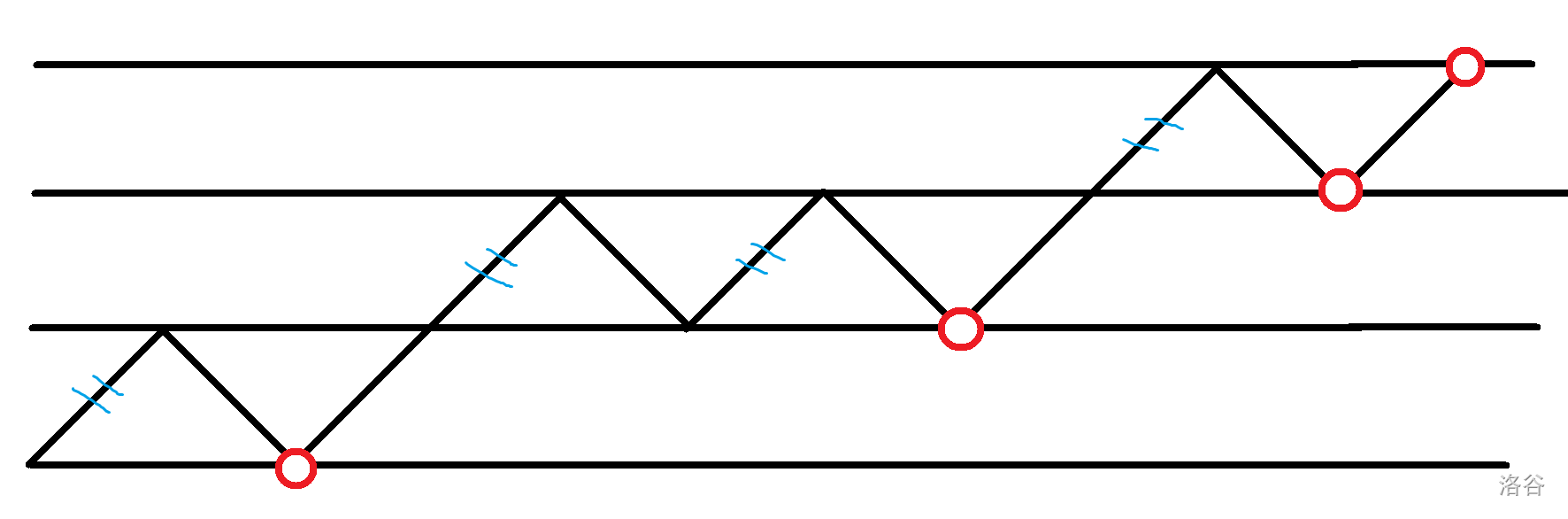
证明,设最大的数为 \(x\),考虑每个数 \(i\) 的出现次数 \(c_i\)。
我们有 \(c_{i}\le c_{i-1}+c_{i+1}\)(除了 \(1\)),因为每个数都由 \(i-1\) 或 \(i+1\) 走来,一个 \(i\) 对应一个 \(i-1\) 或 \(i+1\)。
那么从小的到大的像这样折线放,每放一个 \(i\) 就跟放一个 \(i+1\),直到 \(i\) 不够了就走上面,一定可以涵盖所有情况。
第二种和第一种差不多,我们最后把 \(n\) 减一再算一遍就可以得到第二种。来看第一种。
把每个数最后出现的位置标出来(图中红圈)。会发现剩下的点可以被两两匹配(图中蓝色短线划的线段)。
枚举所有数的最大值 \(x\le m\),以及序列长度 \(l\le n\)。那么除去红点共有 $ \frac{l-x}2$ 组短边。
这些短边要被分配到 \(x-1\) 组里。插板一下就是 \(\binom{\frac{l-x}2+x-2}{x-2}\)。
列个式子
直接计算即可。
B
要求字典序比它小的矩阵个数,考虑求某个位置之前都是一样的,当前位置小于原矩阵,剩下合法随便放的方案数。
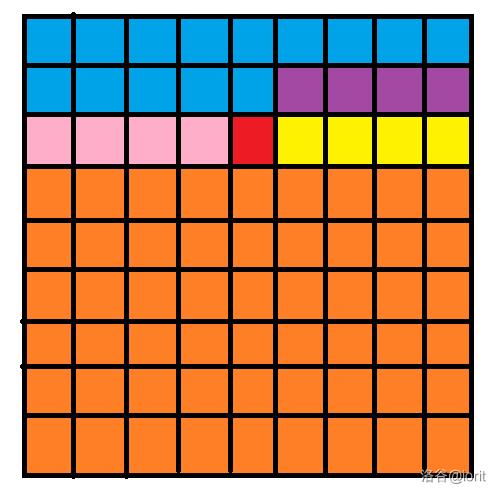
如图,蓝色、紫色、粉色部分都一样,红色格子是决定字典序的格子,黄色、橙色随便放。(满足错排)
设红色格子为 \((i,j)\),设它最后填了 \(x\)。
首先需要满足 \(x<a_{i,j}\)。其次,\(x\) 不能在红色区域出现过。
然后,还要求出黄色部分的方案。具体地,假设黄色还能选的数集合为 \(S\),紫色的 \(a\) 构成的集合为 \(T\),
求出 \(dp_{i,j}\) 表示共有 \(i+j\) 组物品匹配,有 \(i\) 组需要满足错排限制,剩下 \(j\) 组不需要的方案数。
初始:\(dp_{i,0}=f_i,dp_{0,j}=j!\)。\(f\) 是错排方案数,有 \(f_i=if_{i-1}+(-1)^i\)。
然后呢,黄色部分的方案就是 \(dp_{|S\cap T|,|S|+|T|-|S\cap T|}\)
。
现在我们要对每种可能的 \(x\) 求出 \(|S|,|T|\) 和 \(|S\cap T|\)。
事实上,枚举 \(x\) 只会导致 \(S\) 中一个数的变动,不会导致 \(|S|,|T|\) 变化。
考虑 \(|S\cap T|\) 的变化。如果 \(x\) 取到了 \(T\) 中的数会让这个值 \(+1\),否则不变。
那么现在要求不在粉色区域的,且在紫色区域的,且 \(<a_{i,j}\) 的 \(x\) 有多少个。
\(x\) 取到这些数时会使 \(S\cap T\) 少一个数。最后分成两类算即可。
这个 \(x\) 的数量可以考虑维护树状数组,向右移动时顺便维护一下即可。
复杂度 \(\mathcal O(n^2\log n)\)。
C
LIS,LDS 最多只有一个交点。将每个点表示为 \((i,p_i)\),能找到不相交的 LIS,LDS 当且仅当:
序列中存在下标 \(a,b,c,d\),满足 \(a,b\) 是 LIS 中相邻两项,\(c,d\) 是 LDS 中相邻两项,且位置、大小满足下图关系:
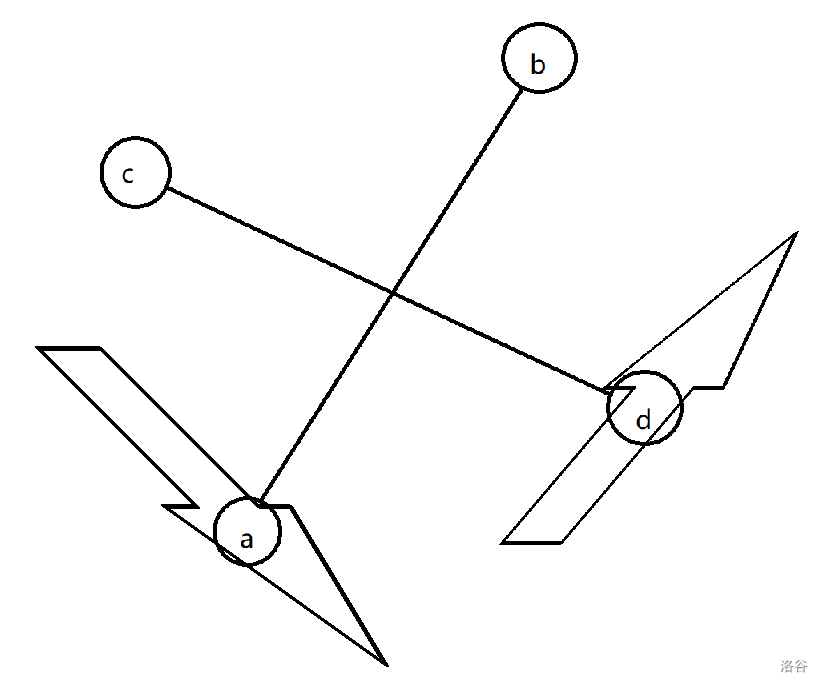
即 \(c<a<b<d,p_a<p_d<p_c<p_b\)。
充分性:显然以上情况,选取包含 \(a,b\) 的 LIS,包含 \(c,d\) 的 LDS 即为答案。
因为 \(a,b\) 是相邻两项,\(c,d\) 也是,所以 LIS,LDS 不会有交点。
必要性:如果存在答案,将 LIS,LDS 中相邻点连线。很显然这两条折线会相交(否则有更长的 LIS / LDS)
假设相交的两条线段,LIS 的端点为 \(a,b\),LDS 的端点为 \(c,d\)。如下图。
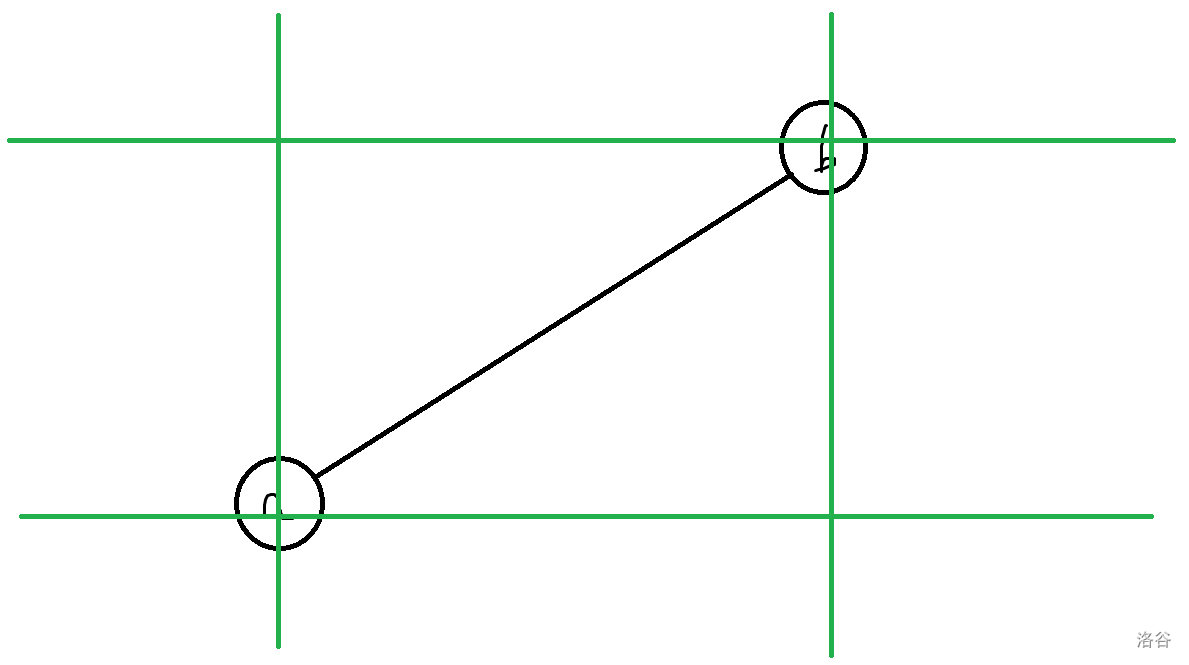
\((a,p_a),(b,p_b)\) 将平面分成了九块。中间一块一定没有点,否则 \(a,b\) 不是相邻两项。
设 \(c<d\)。则 \((c,p_c)\) 可能在左上角一块,正上方,正左方,左下角或者右上角。
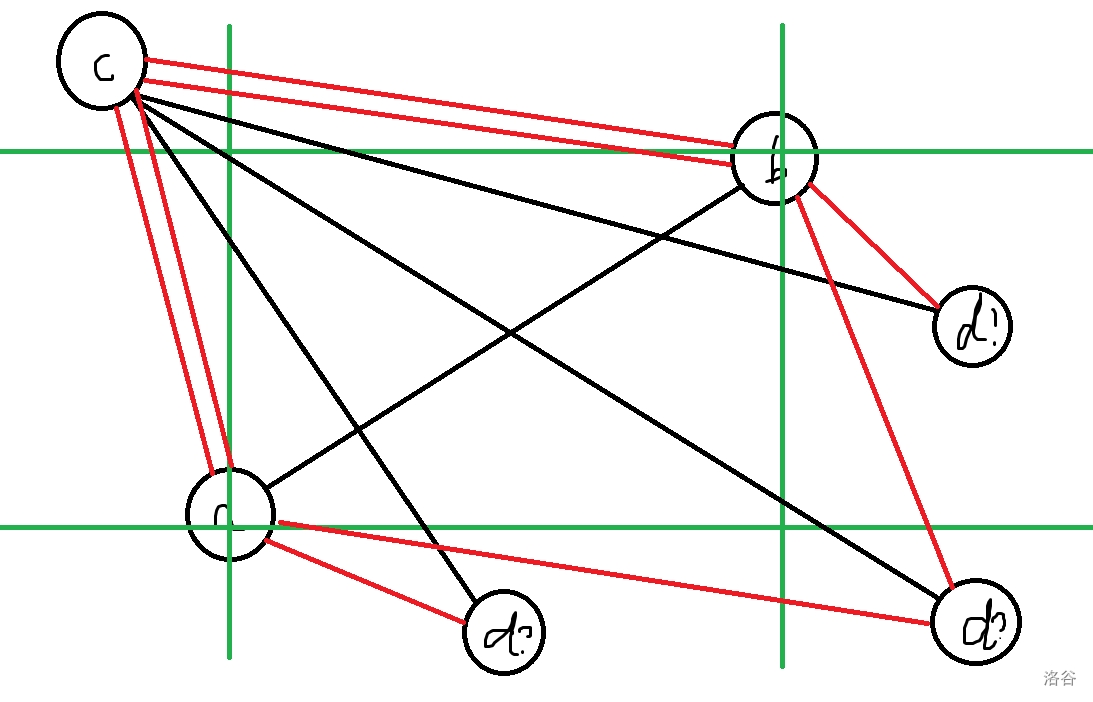
看看左上角。那么 \((d,p_d)\) 可能在下方,右下角或者右方。
如果在下面,你发现 \(c-a-d\) 构成了下降子序列,与 \(c,d\) 在 LDS 中相邻矛盾。
在右边同理,右下方更是使 \(b,c\) 都可以插到中间。
类似地讨论 \(c\) 在其他地方。我们会发现,只有 \(c\) 上 \(d\) 下或者 \(c\) 左 \(d\) 右满足条件。
这两种情况是对称的。至此必要性也证明完毕。

回到这个具有充要性的图。我们现在要做的是,求图中是否存在这么一个结构。
没有的话无解,有的话找一个出来。
注意到求 LIS 的时候,每个 \(b\) 对应多个 \(a\)。这些 \(a\) 的排列一定按图中箭头方向。
(越右上的 dp 值一定越大,可以从左下的转移而来)
而 \(a\) 越往右,合法的 \(c,d\) 只会变多。所以我们对每个 \(b\) 求对应的最大的 \(a\),设为 \(pre_b\)。
同理的,每个 \(c\) 对应一些 \(d\),而这里 \(d\) 越大越能满足条件。因此我们对每一个 \(c\) 维护最大的 \(d\),设为 \(nxt_c\)。
那么对于每一组 \(b,pre_b\),要求满足 \(p_c\in(p_b,p_{pre_b})\) 的 \(c\) 的 \(nxt_c\) 最大值,看看最大值是否大于 \(b\)。
如果大于 \(b\) 则这组 \(a,b,c,d\) 合法。这个简单扫描线,线段树维护最大值即可。
复杂度线性对数。还有,实现时求对称的结构可以直接反转数组再做一遍!/qiang
NOIP2023模拟测试赛(五)
A
\(A_i\) 把值域分成若干段。暴力 dfs 每个数在哪一段。
然后暴力枚举每个数的大小关系。可以求出 LIS 长度。
然后求概率。随便算,长得像一个插板。
复杂度魔幻。\(n\le6\) 且跑不满,基本怎么写都能过。
B
考虑 dp:\(dp_i\) 表示前 \(i\) 个灯笼能照亮的最长前缀。
转移,考虑看第 \(i\) 个灯笼向左还是向右。
如果向右,那么 \(1\sim i\) 一定都是照亮的(才会更长)。
若 \(dp_{i-1}\ge i\),\(dp_{i}\gets\max\{dp_{i-1},i+p_i\}\)。否则 \(dp_{i}\gets dp_{i-1}\)。
如果向左,只需要 \(1\sim i-p_i-1\) 被照亮。
找一个最小的 \(j\) 满足 \(dp_j\ge i-p_i-1\)。那么 \(j+1\sim i-1\) 全部可以向右,转移即
考虑方案如何求。反向推,如果当前 dp 值由向右得到,则自己向右,走到 \(i-1\) 继续推。
否则自己向左,\(j+1\sim i-1\) 全部向右,走到 \(j\)。
复杂度线性对数。
C
即求权值前 \(k\) 大的区间之和。考虑二分,求第 \(k\) 大过程中求出这个和。
设二分的值为 \(x\),要求有多少个区间的权值大于等于 \(x\),以及这些权值的和。
考虑扫描线扫 \(r\)。\(l\) 越大 \([l,r]\) 的权值最小。所以可以双指针。
区间的权值如何快速计算呢?考虑对于每个小的区间 \([a_i,b_i]\),把数轴上 \([a_i,b_i]\) 赋值为 \(i\)。
那么扫到 \(r\) 的时候查询数轴上有多少个 \(\ge l\) 的数即代表 \([l,r]\) 的答案。
考虑颜色段均摊。那么要维护前 \(k\) 大的和,考虑 \(r\) 向右移对所有 \(l\) 的影响:
覆盖 \([a_r,b_r]\),把其中的颜色段提取出来,每段都变成了 \(r\)。
假设这段原先是 \(y\),长度为 \(len\),则 \(l\in[y+1,r]\) 的权值都会加 \(len\)。
总共 \(\mathcal O(n)\) 次区间加。注意到权值随着 \(l\) 增加而减少,区间加完也是减少的。
区间加考虑差分,设 \(d_i=w_i-w_{i-1}\)(\(w\) 为权值),则 \([y+1,r]\) 加 \(len\) 等价于 \(d_{y+1}\) 加 \(len\),\(d_{r+1}\) 减 \(len\)。
设双指针前面的指针为 \(p\),满足 \(\forall l\in[1,p],w_l\ge x\),且 \(p\) 最大。
那么在对权值区间加时,如果区间加的左端点 \(y+1\) 在 \(p\) 左侧,直接计算多出来这段对和、权值的贡献。
否则打上差分的标记,等 \(p\) 走到右边的时候再计算贡献。
至此复杂度 \(\mathcal O(n\log^2n)\)。但注意到每次 ODT 执行的操作是一模一样的,可以在二分前先搞好这些操作。
二分时直接调用转换后的颜色段均摊操作,复杂度即为 \(\mathcal O(n\log n)\)。
NOIP2023模拟测试赛(六)
A
果然是 braintest。有点智障
这个强制在线有明显的漏洞,你发现 lst 会一直是 \(0\),之后某次询问后一直是 \(1\)。
假设变成 \(1\) 的询问序号是 \(k\),那么 \(1\sim k\) 的询问都没被加密。
我们假设一个 \(k\),如果操作完 \(1\sim k\) 图不连通,说明真正的 \(k\) 在这个 \(k\) 之前(或等于)。
那么可以二分,每次暴力删边 check,复杂度线性对数。
此题存在线性做法,具体地改删边为倒序加边,并查集判断是否连通。
B
考虑 \(m=2n\) 的解。我们把矩阵黑白染色,\((1,1)\) 填黑,黑格填上所在行数,白格填上所在列数 \(+n\)。
例如 \(n=6\),如下:
考虑优化,我们先搜索得到一个 \(n=4,m=6\) 的好矩阵,如下:
这里这个矩阵不仅满足原有限制,我们将它横向或者纵向循环移位都会得到好的矩阵。
还是将原矩阵黑白染色,然后我们用上述矩阵拼成一个大矩阵,把黑格子的数加上所在行除以 \(4\) 乘 \(6\),白格子的数加上所在列除以 \(4\) 乘 \(6\)。假设加的这些数称为额外数。
为什么这样是对的?考虑如果存在两组相同的相邻格子,它们上面黑白格子所加的额外数一定相同。
减去这些数,在原来的 \(4\times4\) 矩阵中就会出现两组相同的相邻格子,这与假设矛盾。
因此这样构造一定是对的。
C
考虑 kruskal 求最小生成树的过程,每当加入一条边,如果两端未联通,这条边就在最小生成树中。
设对于一个图,\(F(i)\) 表示只保留边权 \(\le i\) 的边得到的图连通块个数。
那么从 \(F(i-1)\) 到 \(F(i)\),减少的连通块个数即为边权为 \(i\) 的边在最小生成树中的数量。
即,最小生成树权值为 \(\sum_{i=1}^ki(F(i-1)-F(i))\)。
推一下,即为 \(-kF(k)+\sum_{i=0}^{k-1}F(i)\)。
现在对于这个完全图要求 \(E(-kF(k)+\sum_{i=0}^{k-1}F(i))\)。
设 \(f(n,i)=E(F(i))\),\(n\) 表示图的点数,即 \(n\) 个点的完全图,保留 \(\le i\) 的边的期望连通块数。
现在要求的就是 \(-k+\sum_{i=0}^{k-1}f(n,i)\)。为了求 \(f\) 还要套路的求一个东西:
设 \(g(n,i)\) 表示,\(n\) 个点的完全图,保留 \(\le i\) 的边,全图联通的概率。
转移 \(g\):用 \(1\) 减去不连通的概率,枚举 \(1\) 所在的连通块大小 \(j<n\):
乘 \((1-\frac i k)^{j(n-j)}\) 是因为,这个大小为 \(j\) 的连通块不能与其他点有 \(\le i\) 的边。
转移 \(f\):枚举 \(1\) 所在的连通块大小 \(j<n\):
注意到,\(g(n,i)\) 是一个关于 \(i\) 的 \(\frac{n(n-1)}2\) 次多项式。这个可以归纳证明,这里不写了。
同理可以归纳证明,\(f(n,i)\) 也是一个关于 \(i\) 的 \(\frac{n(n-1)}2\) 次多项式。
要求的 \(\sum f(n,i)\) 就是关于 \(i\) 的 \(\frac{n(n-1)}2+1\) 次多项式。
\(n\) 很小,我们可以求出这个前缀和的前 \(\frac{n(n-1)}2+2\) 项,然后拉格朗日插值。
复杂度 \(\mathcal O(n^4)\)。
D
参考这个。板子题不解释
NOIP2023模拟测试赛(七)
我出的




 浙公网安备 33010602011771号
浙公网安备 33010602011771号