p7916-solution

P7916 Solution

link

建立平面图的对偶图，即：对于平面图的每个平面建立它代表的一个点。

对于两个平面，它们之间如果有接触边，则两个平面代表的点之间连一条边，边权为接触边的边权。

对于此题，抄个图：

每个红点都是平面代表的点，当然中间两个平面也应该有代表的点，但是因为两侧颜色不同所以不用建，一会会讲。

中间 \(15\) 格的平面也是 \(15\) 个点。

考虑 \(k=2\) 的情况，这时候外面只有两个平面，假设代表的点为 \(s,t\)。

如果两个询问点同色则显然答案为 \(0\)。否则，考虑用一条折线切开这个平面图，一半黑色一半白色。

如果不是这样划分一定不优，可以通过翻转一部分颜色得到更优的。

这条折线想要权值最小，其实就是求 \(s\) 到 \(t\) 的最短路。

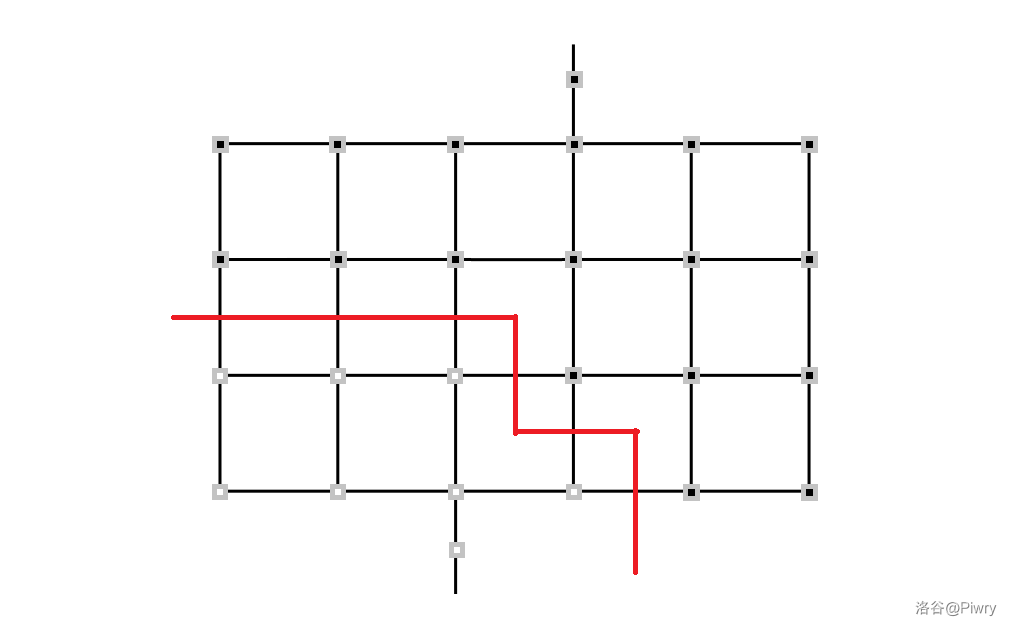
如图，左边大平面是 \(s\)，右边大平面是 \(t\)，容易发现就是最短路。

考虑 \(k>2\)。对于一种染色方案，将划分黑白的若干折线画出来。

首先折线一定没有环，否则直接去掉这个环答案减小。

然后每个点的度数一定是偶数，毕竟是黑白染色。

接着对于两条射线都同色的平面，显然它的度数应为 \(0\)，因为既然两侧同色都不需要划分开。

这样就可以将划分线变成两侧不同色平面的两两配对问题。

而且配对一定不存在交叉，否则换一下顺序就一样了。

这样就可以区间 \(dp\)，转移要么枚举断点要么让 \(l,r\) 配对，权值是 \(l,r\) 最短路。

复杂度 \(\Theta(k^3+knm\log(nm))\)。