cf1473g-solution

CF1473G Solution

link

题意：

现在有一条由许多瓷砖拼成的路，类似下图所示：

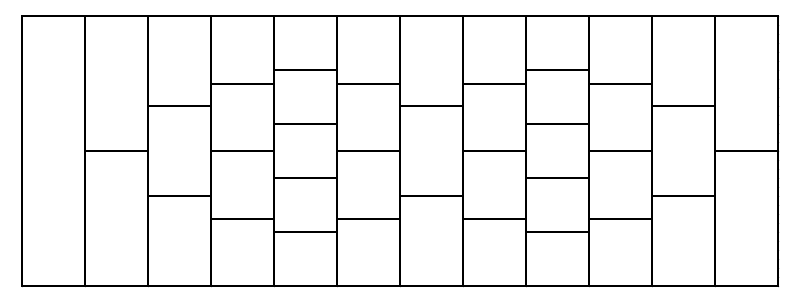
它的构成方式如下：

• 每一列的所有瓷砖都全等，第一列仅有 \(1\) 块瓷砖。

• 接下来 \(a_1\) 列，每列的瓷砖数量都比上一列多 \(1\)。

• 接下来 \(b_1\) 列，每列的瓷砖数量都比上一列少 \(1\)。

• 接下来 \(a_2\) 列，每列的瓷砖数量都比上一列多 \(1\)。

• 接下来 \(b_2\) 列，每列的瓷砖数量都比上一列少 \(1\)。

• ...

• 接下来 \(a_n\) 列，每列的瓷砖数量都比上一列多 \(1\)。

• 接下来 \(b_n\) 列，每列的瓷砖数量都比上一列少 \(1\)。

现在你在第一块瓷砖上，你想要走到最后一列（任意一块瓷砖）上，

且每次只能走到下一列与当前瓷砖接触的任意一块瓷砖。

请你求出方案数，对 \(998244353\) 取模。

\(n\le1000,1\le a_i,b_i\le10^5,|a_i-b_i|\le 5\)。

---

这个瓷砖上行走的方式有点诡异。我们考虑转换一下题意。

根据直觉，假设这一列的瓷砖比下一列少，那么从这列某个瓷砖到下一列的瓷砖选择仅有两种。

看看样例的图至少是正确的：

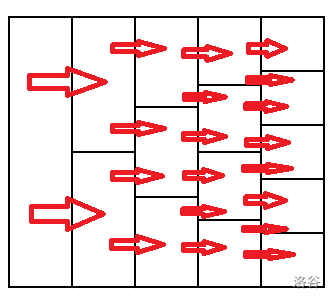
下面进行证明。

假设这一列有 \(x\) 个瓷砖，那么下一列就有 \(x+1\) 个瓷砖。

显然这列的瓷砖至少都有两个选择。因为它们比下一列的瓷砖大。

现在我们假设这一列的第 \(i\) 个瓷砖有至少 \(3\) 个选择，

那么显然下一列至少有一个瓷砖是会被这一列的第 \(i\) 个瓷砖”包含“的。假设它是第 \(j\) 个瓷砖。

如图：

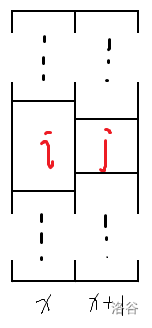
那么可以列出不等式

\[\begin{cases} \dfrac{i-1}x<\dfrac{j-1}{x+1}\cdots\cdots\cdots\mathbf I\\\\ \dfrac{x-i}x<\dfrac{x+1-j}{x+1}\cdots\cdots\cdots\mathbf{II} \end{cases}\]

\(\mathbf I\) 等价于 \((i-1)(x+1)<x(j-1)\)

即 \(ix-x+i-1<jx-x\)

即 \(ix+i-1<jx\cdots\cdots\cdots\mathbf{III}\)

\(\mathbf{II}\) 等价于 \(1-\dfrac i x<1-\dfrac j{x+1}\)

即 \(\dfrac i x>\dfrac j{x+1}\)

即 \(i(x+1)>jx\cdots\cdots\cdots\mathbf{IV}\)

\(\mathbf{III},\mathbf{IV}\) 可得 \(ix+i-1<jx<ix+i\)。

但是 \(ix+i-1\) 和 \(ix+i\) 是两个相邻自然数，在其中是不可能再夹一个自然数的。

故假设矛盾，即这列的瓷砖到下一列的选择仅有两种。\(\blacksquare\)

接下来就好办了，因为选择仅有两种，原题的每一段都等价于下面的图：

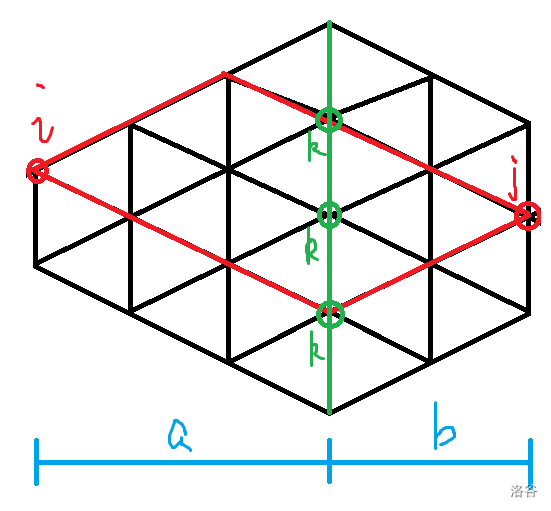
这里把瓷砖抽象成了点，每次可以向右边相邻的点走。

那么想要知道从 \(i\) 到 \(j\) 有多少方案，直接看可能看不出来，那么我们可以枚举中间的 \(k\) 点：

\[\begin{aligned} \sum_k\binom a{k-i}\binom b{k-j} &=\sum_k\binom a{k-i}\binom b{b-k+j}\\ &=\binom{a+b}{b-i+j} \end{aligned}\]

接下来我们考虑 dp：设 \(dp_{pos,i}\) 表示到第 \(pos\) 组瓷砖铺完后最后一列的第 \(i\) 块瓷砖的方案数。

初始化：\(dp_{0,1}=1\)。

转移：

\[dp_{pos,i}=\sum_jdp_{pos-1,j}\binom{a_{pos}+b_{pos}}{b_{pos}-j+i} \]

对于当前的 \(pos\)，设 \(f_x=\dbinom{a+b}{b+x}\)，则

\[dp_{pos,i}=\sum_jdp_{pos-1,j}f_{i-j} \]

容易看出这是个卷积形式。于是用 NTT 优化，最后复杂度 \(\mathcal O(n^2\log n)\)。