cf1163f-solution

CF1163F Solution

link

考虑求出从 $1$ 和 $n$ 开始的最短路树，如下图。

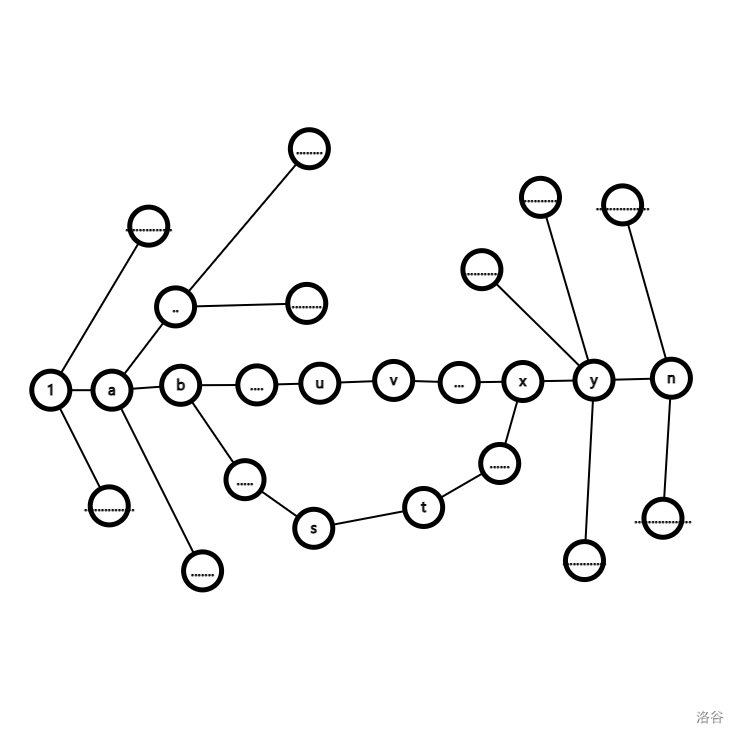
$1\to a\to b\to\cdots\to x\to y\to n$ 是 $1$ 到 $n$ 的最短路。

分类讨论：

• 如果修改的边 $(u,v)$ 不在最短路上，

答案就是原来最短路长和过 $(u,v)$ 的最短路的最小值，这个容易预处理。从 $1,n$ 分别跑一遍最短路即可。

• 如果修改的边 $(u,v)$ 在最短路上，

$1)$ 如果边权变小，最短路径不变。长度修改一下就好。

$2)$ 如果边权变大，

考虑过 $(u,v)$ 的最短路和不过 $(u,v)$ 的最短路。前者的路径就是原来最短路的路径，可以直接计算。

不过 $(u,v)$ 的最短路：考虑最终路径一定是先沿 $1\to n$ 的最短路走一段，然后从某个点 $b$ 走出这条主干，然后沿 $1$ 的最短路树走一段，然后跳某条边 $(s,t)$ 跳到 $n$ 的最短路树上，然后走回 $1\to n$ 的最短路到达 $n$。

从图中看就是 $1\to b\to s\to t\to x\to n$，而且要满足 $b$ 在 $u$ 前面， $x$ 在 $v$ 后面。

于是对于每条不在最短路中的边，求出它的 $u$ 在 $1$ 的最短路树上往上跳到的主干对应位置（相当于 $s$ 和 $b$），$v$ 在 $n$ 的最短路树上跳到位置。

塞进一个数据结构里，这样每次查询相当于查询所有 $l\le x,r\ge x+1$ 的 $dis$ 最小值。这就是一个二维数点。

当然也可以考虑每个 $[l,r]$ 对 $[l,r-1]$ 的 $x$ 有 $dis$ 的贡献，搞一个区间取 min，最后直接预处理每条边的答案。

复杂度 $O(n\log n)$，若 $n,m$ 同阶。

Code

#include <bits/stdc++.h>
#define LL long long
#define sl(n) strlen(n)
#define endline puts("")
#define pii pair<int , int>
#define pr_q priority_queue
#define DEBUG puts("DEBUG.")
using namespace std;
const int N = 2e5 + 10;
const LL inf = ~0ull >> 2;
int n,m,q,cnt = 1,head[N];
struct edge
{
	int u,v,w;
	int nxt;
}edge[N << 1];
void add(int u , int v , int w = 0)
{
	++cnt,edge[cnt].u = u,edge[cnt].v = v,edge[cnt].w = w;
	edge[cnt].nxt = head[u],head[u] = cnt;
}
bool inp[N],ine[N << 1];
struct shortest_path
{
	LL dis[N];
	int pre[N],epre[N];
	bool vis[N];
	struct node
	{
		LL dis;
		int num;
		bool operator < (const node &x) const
			{return x.dis < dis;}
	};
	void dijk(int s)
	{
		memset( dis , 32 , sizeof(dis) );
		pr_q<node> q;
		dis[s] = 0,q.push( (node){0 , s} );
		while( !q.empty() )
		{
			int u = q.top().num;
			q.pop();
			if( vis[u] )
				continue;
			vis[u] = true;
			for(int i = head[u];i;i = edge[i].nxt)
			{
				int v = edge[i].v;
				if(dis[v] > dis[u] + edge[i].w)
				{
					dis[v] = dis[u] + edge[i].w,pre[v] = u,epre[v] = i;
					q.push( (node){dis[v] , v} );
				}
			}
		}
	}
}D[2];
vector<int> G[2][N];
int bel[2][N];
void dfs0(int u)
{
	if( inp[u] )
		++bel[0][u];
	for( auto v : G[0][u] )
	{
		bel[0][v] = bel[0][u];
		dfs0(v);
	}
}
void dfs1(int u)
{
	if( inp[u] )
		--bel[1][u];
	for( auto v : G[1][u] )
	{
		bel[1][v] = bel[1][u];
		dfs1(v);
	}
}
struct node
{
	LL mn,tag;
}t[N << 2];
LL ans[N];
void build(int o , int l , int r)
{
	t[o].mn = t[o].tag = inf;
	if(l == r)
		return ;
	int mid = l + r >> 1;
	build(o << 1 , l , mid);
	build(o << 1 | 1 , mid + 1 , r);
}
void push_down(int o)
{
	if(t[o].tag == inf)
		return ;
	LL &k = t[o].tag;
	o <<= 1;
	t[o].tag = min(t[o].tag , k),t[o].mn = min(t[o].mn , k);
	++o;
	t[o].tag = min(t[o].tag , k),t[o].mn = min(t[o].mn , k);
	k = inf;
}
void modify(int sl , int sr , int o , int l , int r , LL k)
{
	if(sl > sr)
		return ;
	if(sl <= l && r <= sr)
	{
		t[o].tag = min(t[o].tag , k),t[o].mn = min(t[o].mn , k);
		return ;
	}
	push_down(o);
	int mid = l + r >> 1;
	if(mid >= sl)
		modify(sl , sr , o << 1 , l , mid , k);
	if(mid + 1 <= sr)
		modify(sl , sr , o << 1 | 1 , mid + 1 , r , k);
	t[o].mn = min(t[o << 1].mn , t[o << 1 | 1].mn);
}
void dfs(int o , int l , int r)
{
	if(l == r)
	{
		ans[l] = t[o].mn;
		return ;
	}
	push_down(o);
	int mid = l + r >> 1;
	dfs(o << 1 , l , mid),dfs(o << 1 | 1 , mid + 1 , r);
}
signed main()
{
	cin >> n >> m >> q;
	for(int i = 1,u,v,w;i <= m;i++)
		scanf("%d%d%d" , &u , &v , &w),add(u , v , w),add(v , u , w);
	D[0].dijk(1),D[1].dijk(n);
	int u = n;
	while(u)
		ine[ D[0].epre[u] ] = ine[D[0].epre[u] ^ 1] = 1,inp[u] = 1,u = D[0].pre[u];
	for(int i = 1;i <= n;i++)
		for(int j = 0;j <= 1;j++)
			G[j][ D[j].pre[i] ].push_back(i);
	dfs0(1),bel[1][n] = bel[0][n] + 1,dfs1(n);
	int len = bel[0][n] - 1;
	build(1 , 1 , len);
	for(int i = 2;i <= cnt;i++)
	{
		if( ine[i] )
			continue;
		int l = bel[0][edge[i].u],r = bel[1][edge[i].v];
		LL k = D[0].dis[edge[i].u] + edge[i].w + D[1].dis[edge[i].v];
		modify(l , r - 1 , 1 , 1 , len , k);
	}
	dfs(1 , 1 , len);
	while(q--)
	{
		int x,y;
		scanf("%d%d" , &x , &y);
		int u = edge[x * 2].u,v = edge[x * 2].v,w = edge[x * 2].w;
		if( ine[x * 2] )
			if(y > w)
				printf( "%lld\n" , min( D[0].dis[n] - w + y , ans[ min( bel[0][u] , bel[0][v] ) ] ) );
			else
				printf("%lld\n" , D[0].dis[n] - w + y);
		else
			if(y > w)
				printf( "%lld\n" , D[0].dis[n] );
			else
				printf( "%lld\n" , min({D[0].dis[n] , D[0].dis[u] + y + D[1].dis[v] , D[0].dis[v] + y + D[1].dis[u]}) );
	}
	return 0;
}