Java KMP算法总结
KMP 算法:比BF算法更为高效,BF算法的时间复杂度是:O(mn)
m代表主串的长度,n 代表子串的长度。而KMP的话,时间复杂度就变为 O(m+n);
KMP 和 BF 唯一不同,KMP主串的i并不会回退,并且j也不会移动到0号位置。那么会退到哪里呢??
![]()
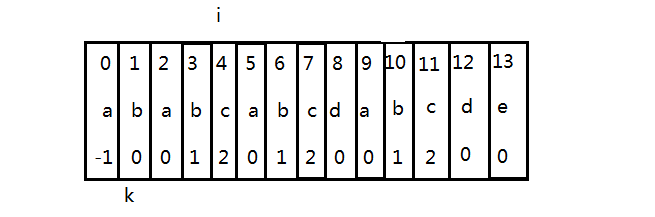
这时候,对应的 next 数组:-1,0,0,0,1,2 next[2] 对应的就是 c.
假定主串 S 子串 P:
P0...PK-1 = Px...Pj-1
则有:P0...PK-1 = Pj-k...Pj-1
假如每一次不成功,肯定会有对应的一个K值。那么如何保存这些值?怎么求这些值?那这就是
KMP 的精髓。在这里就会出现新的东西,那就是 next 数组;也就是用 next[j] = k;来表示,不同的 j 来对应一个 K 值,
这个K就是将来要移动的j要移动的位置。
K值求法:找到匹配成功部分的两个相等的真子串(不包含本身),一个以下标 0 开始,另一个以 j-1 下标结尾。
不管什么数据 next[0] = -1;next[1] = 0;
得到 next 数组:通过 next[i]的值,通过一系列转换得到 next[i+1]得值,那么我们就能够实现这部分。
怎么做?
首先假设:next[i] = k 成立,那么,就有这个式子成立:P0...Pk-1 = Px...Pi-1;
得到:P0...Pk-1 = Pi-k..Pi-1;
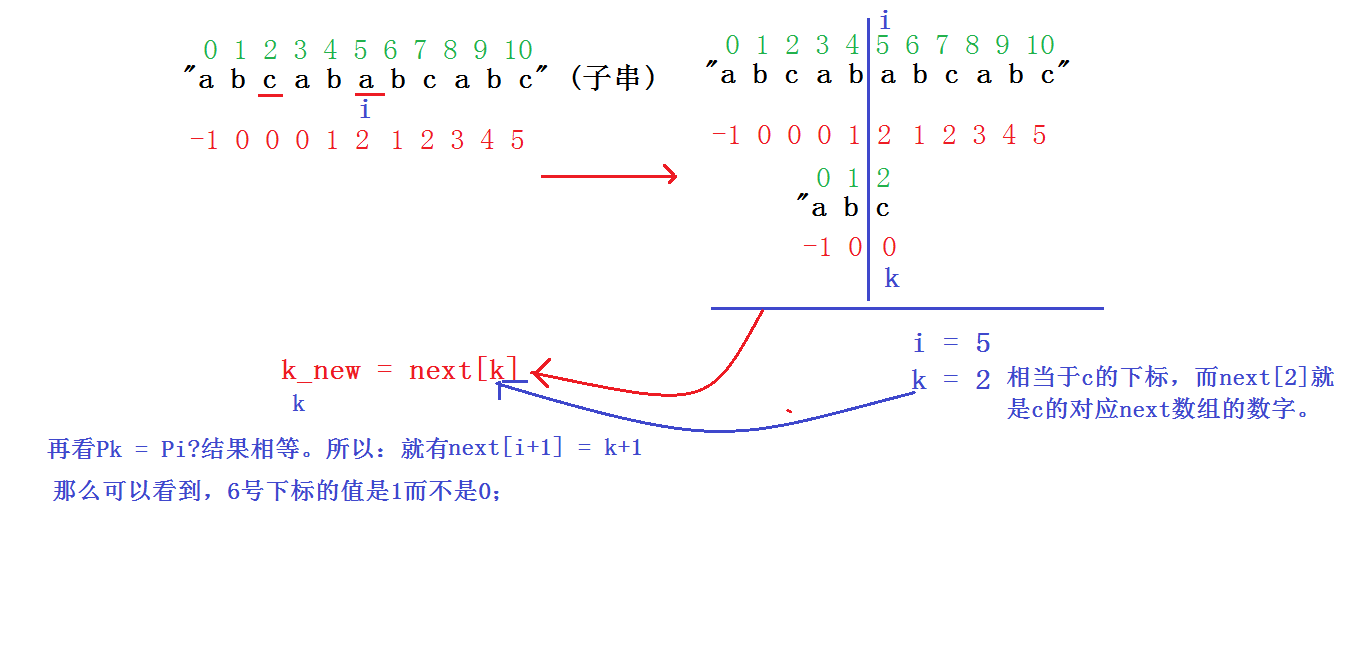
假设如果 Pk = Pi: 得到 P0...Pk = Pi-k..Pi;那这个就是 next[i+1] = k+1;
那么:Pk != Pi 呢?看这个例子:abcababcabc
package string; public class KMPDemo { //得到next数组 public static void getNext(int[]next,String sub){ next[0]=-1; next[1]=0; int i=2; int k=0; while(i<sub.length()){
if(k==-1||sub.charAt(k)==sub.charAt(i-1)){//Pk==P(i-1)
next[i]=k+1;
i++;
k++;
}else{
k=next[k]; } } } public static int KMP(String str,String sub,int pos ){ if(pos<0||pos>str.length()||sub.length()>str.length()){ return -1; } //开始查找 int i=pos; int j=0; int[]next=new int[sub.length()]; getNext(next,sub); //遍历主串和子串 while(i<str.length()&&j<sub.length()){ //判断对应下表是否相同 if(j==-1l||str.charAt(i)==sub.charAt(j)){ i++; j++; }else{ j=next[j];//j返回到next【j】处 } } //那种情况说明了子串在主串的位置 if(j>=sub.length()){// return i-j;//子串出现在主串上的某一位置 }else{ return -1;//子串不在主串上 } } public static void main(String[] args) { // TODO Auto-generated method stub String str="abcabcdabcd"; String sub="dab"; int index=KMP(str,sub,0); System.out.println(index); } }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号