多元函数二阶偏导数的矩阵表示

几天前,求解二维 Laplace 方程,为了方便,欲用坐标变换把直角坐标化为极坐标。花费了不小的力气才得到结果,所以就寻思把二阶偏导的内容整理一下,便得出此技巧。


发现过程大致如下,整理资料的时候,顺手尝试了这样一道题目:


解题过程就是普通的求导运算得到的结果是:
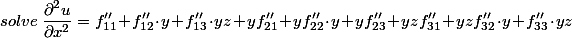
看着这么有规律的下标,不用说,各位一定想到了矩阵,而且是3阶方阵......
为了得到更一般的规律,必须用符号再一次的进行运算。对于多元复合函数 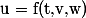 求其二阶偏导数:
求其二阶偏导数:
- 一阶偏导数为:
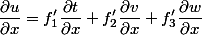
- 进一步求二阶偏导数:
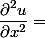
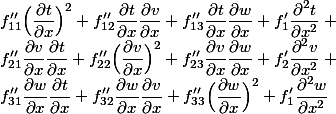
- 上面式子的结构很清晰,是一个完全二次型加上两个向量的积:

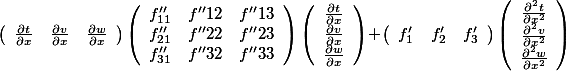
也许这里想一下矩阵的运算法则和偏微分的法则,数学素养可能会稍有提升…… - 同理有:
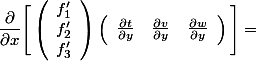
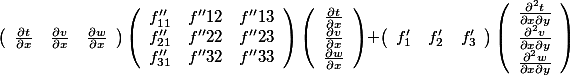
类似地,可以依次得出其他二次偏导的结果...
- 另外,值得一提的是,这种方法也适用于二中间变量,二自变量,甚至稍加修改便可以推广 到求n阶偏导... 例如,
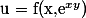 和,
和,  的二阶偏导数,都可以在片刻得到结果。
的二阶偏导数,都可以在片刻得到结果。


回到初始,把二维直角坐标的 Laplace 方程 化为极坐标:
- 二维直角坐标 Laplace 方程 数学形式如下:
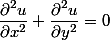
值得注意的是,它的物理解释简单明了。表示热或者物质扩散在某种特殊的情况下处于稳定状态, 或者说变化相当小,可以看作与时间无关。
- 根据二阶的二次偏导公式:
- 对极角:

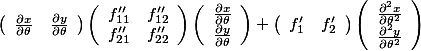
- 对极径:

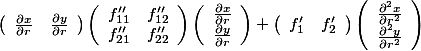
- 对极角:
- 根据坐标变换公式:
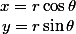
- 可以求出以下结果:
- 把4.的结果代入到2.:
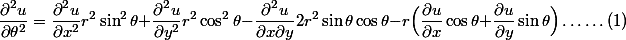
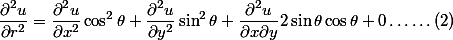
- (2)加上(1)除以r的平方:
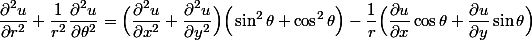
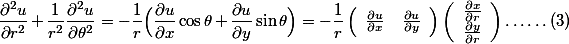
- 因为(在4.里第一个等式):
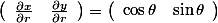
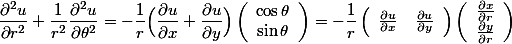
- 根据:
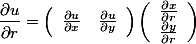
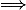

结果已经得到,文章也该结束了……


本文是为了测试数学公式的输出问题所写,内容没有太多新意和思想,大家见谅!如果发现文中 错误,请一定要点击下面链接发邮件与我交流
给我QQ发邮件(1074193407@qq.com) 给我Hotmail发邮件(yang31415@hotmail.com)
如果配置了OUTLOOK可以直接点击上面链接,如果没有配置直接向以上邮箱地址发邮件即可。



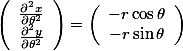

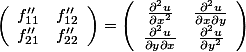
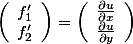


 浙公网安备 33010602011771号
浙公网安备 33010602011771号