第10章数值计算

10.1 线性方程组的解法

函数	功能
rank(A)	求A的秩，即A中线性无关的行数和列数
det(A)	求A的行列式
inv(A)	求A的逆矩阵。如果A是奇异矩阵或近似奇异矩阵，则会给出一个错误信息
pinv(A)	求A的伪逆。如果A是mn矩阵，则伪逆的大小为nm。对于非奇异矩阵A来说，有pinv(A)=inv(A)
trace(A)	求A的迹，即对角线元素之和

x=A\b % 求解系统Ax=b
X=A\B % 求解系统AX=B，其中B=(b1 b2 ... bp)

10.1.1 直接解法

>> A=[1 3 -3 -1; 3 -6 -3 4; 1 5 -9 -8];
>> B=[1 4 0]';
>> X=A\B % 一个特解近似值

X =

         0
   -0.0000
   -0.5333
    0.6000

10.1.2 逆矩阵法

x=A^-1*b
x=inv(A)*b

>> A=[1 2; 3 4]; b=[-1; -1];
>> x=inv(A)*b

x =

    1.0000
   -1.0000

>> x=A^-1*b

x =

    1.0000
   -1.0000

>> A=[1 2; 2 4]; b=[-1; -1];
>> x=A^-1*b % 警告：矩阵为奇异工作精度

x =

  -Inf
  -Inf

10.1.3 利用矩阵的LU分解求解

[L,U]=lu(A)

>> A=[4 2 -1; 3 -1 2; 11 3 1];
>> B=[2 10 8]';
>> D=det(A)

D =

  -10.0000

>> [L,U]=lu(A)

L =

    0.3636   -0.5000    1.0000
    0.2727    1.0000         0
    1.0000         0         0


U =

   11.0000    3.0000    1.0000
         0   -1.8182    1.7273
         0         0   -0.5000

>> X=U\(L\B)

X =

    4.0000
  -10.0000
   -6.0000

10.1.4 求线性方程组的其他解法

10.1.4.1 Jacobi迭代法

新建“函数 jacobi.m 文件”

function jacobi(A,B,P,delta,max1) % A-系数矩阵；B-常数项；P-初始值；delta-允许误差；maxl-最大迭代次数
N=length(B);
for k=1:max1
    for j=1:N
        X(j)=(B(j)-A(j,[1:j-1,j+1:N])*P([1:j-1,j+1:N]))/A(j,j);
    end
    err=abs(norm(X'-P));
    relerr=err/(norm(X)+eps);
    P=X';
    k; P';
    if (err<delta)||(relerr<delta)
        break
    end
end
X=X'

>> A=[3 1 -1; 4 8 1; 3 1 6];
>> B=[6 -20 15]';
>> x0=[1 2 1]'; % 设定初始值
>> jacobi(A,B,x0,1e-5,50);

X =

    3.9786
   -4.6500
    1.2857

10.1.4.2 Gauss-Seidel迭代法

新建“函数 gseid.m 文件”

function jacobi(A,B,P,delta,max1) % A-系数矩阵；B-常数项；P-初始值；delta-允许误差；maxl-最大迭代次数
N=length(B); % X=zeros(N,1)
for k=1:max1
    for j=1:N
        if j==1
            X(1)=(B(1)-A(1,2:N)*P(2:N))/A(1,1);
        elseif j==N
            X(N)=(B(N)-A(N,1:N-1)*(X(1:N-1))')/A(N,N);
        else
            X(j)=(B(j)-A(j,1:j-1)*X(1:j-1)-A(j,j+1:N)*P(j+1:N))/A(j,j);
        end
    end
    err=abs(norm(X'-P));
    relerr=err/(norm(X)+eps);
    P=X';
    k; P';
    if (err<delta)||(relerr<delta)
        break
    end
end
X=X'

>> A=[3 1 -1; 4 8 1; 3 1 6];
>> B=[6 -20 15]';
>> x0=[1 2 1]'; % 设定初始值
>> gseid(A,B,x0,1e-5,60);

X =

    3.9786
   -4.6500
    1.2857

10.2 插值

10.2.1 一维数据插值

vq=interp1(x,v,xq) % 使用线性插值返回一维函数在特定查询点的插入值
vq=interp1(x,v,xq,method) % 指定备选插值方法
vq=interp1(x,v,xq,method,extrapolation) % 指定外插策略计算落在x域范围外的点

vq=interp1(v,xq) % 返回插入的值，并假定一个样本点坐标默认集
vq=interp1(v,xq,method) % 指定备选插值方法中的任意一种，并使用默认样本点
vq=interp1(v,xq,method,extrapolation) % 指定外插策略，并使用默认样本点
pp=interp1(x,v,method,'pp') % 使用method算法返回分段多项式形式的v(x)

>> x=linspace(0,2*pi,40);
>> y=cos(x.^2);
>> val=interp1(x,y,[0 pi/2 3]) % 用interp1计算中间点的函数值

val =

    1.0000   -0.7677   -0.8200

>> cor=cos([0 pi/2 3].^2) % 与用cos计算得到的正确结果进行比较

cor =

    1.0000   -0.7812   -0.9111

10.2.2 二维数据插值

Vq=interp2(X,Y,V,Xq,Yq) % 使用线性插值返回双变量函数在特定查询点的插入值

Vq=interp2(V,Xq,Yq) % 假定一个默认的样本点网格

Vg=interp2(V) % 将每个维度上样本值之间的间隔分割一次形成优化网格，并返回插入值
Vq=interp2(V,k) % 将每个维度上样本值之间的间隔反复分割k次形成优化网格,并在这些网格上返回插入值，即在样本值之间生成2^k-1个插值点
Vq=interp2(___,method) % 指定备选插值方法
Vq=interp2(___,method,extrapval) % 指定标量值extrapval

>> [X,Y]=meshgrid(-3:3);
>> V=peaks(7);
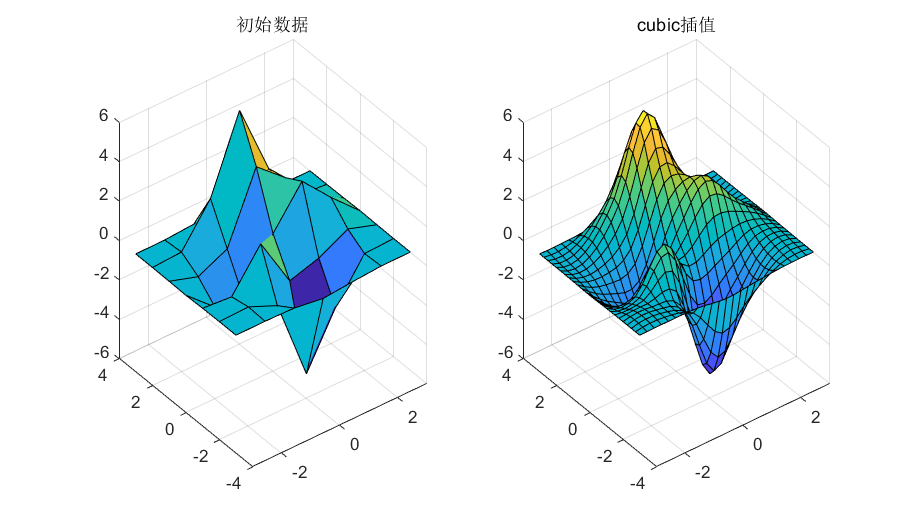
>> subplot(1,2,1); surf(X,Y,V)
>> title('初始数据');
>> [Xq,Yq]=meshgrid(-3:0.25:3); % 创建间距为0.25的查询网格
>> Vq=interp2(X,Y,V,Xq,Yq,'cubic'); % 对查询点插值，并指定三次插值
>> subplot(1,2,2); surf(Xq,Yq,Vq) % 绘制结果
>> title('cubic插值');

10.2.3 三维及多维数据插值

Vq=interp3(X,Y,Z,V,Xq,Yq,Zq)
Vq=interp3(V,Xq,Yq,Zq)
Vg=interp3(V)
Vq=interp3(V,k)
Vq=interp3(___,method)
Vq=interp3(___,method,extrapval)

10.2.4 三次样条数据插值

s=spline(x,y,xq) % 返回与xg中的查询点对应的三次样条插值s的向量
pp=spline(x,y) % 返回一个分段多项式结构体，以用于ppval和样条工具unmkpp

>> x=-3:3;
>> y=[-1 -1 -1 0 1 1 1];
>> xq1=-3:.01:3;
>> p=pchip(x,y,xq1);
>> s=spline(x,y,xq1);
>> m=makima(x,y,xq1);
>> plot(x,y,'o',xq1,p,'-',xq1,s,'-.',xq1,m,'--')
>> legend('Points','pchip','spline','makima','Location','SouthEast')

10.2.5 快速傅里叶变换插值

y=interpft(X,n) % 在X中内插函数值的傅里叶变换以生成n个等间距的点
y=interpft(X,n,dim) % 沿维度dim运算

10.2.6 对二维或三维散点数据插值

vq=griddata(x,y,v,xq,yq) % 拟合v=f(x,y)形式的曲面与向量(x,y,v)中的散点数据，即在(xq,yq)指定的点对曲面进行插值并返回插入的值vq
vg=griddata(x,y,z,v,xq,yq,zq) % 拟合v=f(x,y,z)形式的超曲面
vq=griddata(___,method) % 指定计算vq所用的插值方法
[Xq,Yq,vq]=griddata(x,y,v,xq,yq)
[Xq,Yq,vq]=griddata(x,y,v,xq,yq,method) % 额外返回Xq、Yq，包含查询点的网格坐标

>> x=rand(20,1); % 生成有20个元素的向量，元素值随机分布在0~1内
>> y=rand(20,1); % 生成有20个元素的向量，元素值随机分布在0~1内
>> z=rand(20,1); % 生成有20个元素的向量，元素值随机分布在0~1内
>> stps=0:0.02:1; % 向量A的值在[0,1]区间
>> [X,Y]=meshgrid(stps); % 生成一个[0,1]*[0,1]坐标网络
>> Z1=griddata(x,y,z,X,Y); % 线性插值
>> Z2=griddata(x,y,z,X,Y,'cubic'); % 三次插值
>> Z3=griddata(x,y,z,X,Y,'nearest'); % 最邻近插值
>> Z4=griddata(x,y,z,X,Y,'v4'); % MATLAB中的插值方法
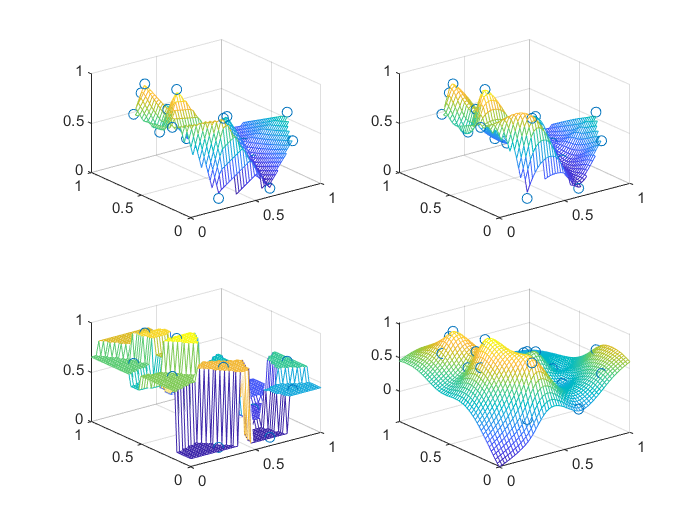
>> subplot(2,2,1); mesh(X,Y,Z1); % 第一个子图中画曲面网格
>> hold on % 保持当前图形
>> plot3(x,y,z,'o'); % 画出数据点
>> hold off % 释放图形
>> subplot(2,2,2); mesh(X,Y,Z2); % 第二个子图中画曲面网格
>> hold on % 保持当前图形
>> plot3(x,y,z,'o'); % 画出数据点
>> hold off % 释放图形
>> subplot(2,2,3); mesh(X,Y,Z3); % 第三个子图中画曲面网格
>> hold on % 保持当前图形
>> plot3(x,y,z,'o'); % 画出数据点
>> hold off % 释放图形
>> subplot(2,2,4); mesh(X,Y,Z4); % 第四个子图中画曲面网格
>> hold on % 保持当前图形
>> plot3(x,y,z,'o'); % 画出数据点
>> hold off % 释放图形

10.3 曲线拟合

p=polyfit(x,y,n) % 返回多项式的系数，是一个长度为n+1的向量p,用最小二乘法对输入的数据x、y用n阶多项式进行逼近
[p,s]=polyfit(x,y,n) % 额外返回误差分析报告，并保存在结构体变量s中

>> x=[1 2 3 4 5];
>> y=[1.2 1.8 2.4 3.9 4.5];
>> [p,s]=polyfit(x,y,1)

p =

    0.8700    0.1500


s = 

  包含以下字段的 struct:

           R: [2×2 double]
          df: 3
       normr: 0.4930
    rsquared: 0.9689

>> y1=polyval(p,x);
>> plot(x,y1); hold on;
>> plot(x,y,'b*');

>> clear,clf
>> x=-2:0.2:2;
>> y=1./(1+2*x.^2);
>> p4=polyfit(x,y,4);
>> p10=polyfit(x,y,10); % 用向量x和y中元素拟合不同次数的多项式
>> xcurve=-2:0.02:2;
>> p4curve=polyval(p4,xcurve); % 计算在这些x点处的多项值
>> p10curve=polyval(p10,xcurve);
>> plot(xcurve,p4curve,'r--',xcurve,p10curve,'b-.',x,y,'ko');
>> legend('L4(x)','L10(x)','精确值');

>> clear,clf
>> x=0:0.2:2;
>> y=sin(x);
>> p=polyfit(x,y,8); % 用x和y在[0,2]区间上拟合
>> x1=0:0.2:6;
>> y1=polyval(p,x1);
>> y2=sin(x1);
>> plot(x1,y1,'kx',x1,y2,'k-') % 在[0,6]区间上画图
>> legend('polyfit','sin(x)');

10.4 数值积分

10.4.1 梯形法数值积分

T=trapz(Y) % 用等距梯形法近似计算Y的积分
T=trapz(X,Y) % 用梯形法计算Y在X点上的积分
T=trapz(___,dim) % 沿着dim指定的方向对Y进行积分，若参量中包含X，则应有length(X)=size(Y,dim)

>> X=-1:.1:1;
>> Y=1./(1+2*X.^2);
>> T=trapz(X,Y)

T =

    1.3503

>> x=-3:.1:3;
>> y=-5:.1:5;
>> [X,Y]=meshgrid(x,y); % 创建由域值构成的网络
>> F=X.^2+Y.^2; % 建立网络上的函数
>> T=trapz(y,trapz(x,F,2)) % 对数值数据的数组执行二重积分运算

T =

  680.2000

10.4.2 自适应辛普森积分法

q=quad(fun,a,b) % 近似地从a到b计算函数fun的数值积分，默认误差为1.0e-6
q=quad(fun,a,b,tol) % 用指定的绝对误差tol代替默认误差
q=quad(fun,a,b,tol,trace) % 打开诊断信息的显示

>> fun=inline('x.^2./(x.^3-x.^2+3)');
>> Q1=quad(fun,0,2)

Q1 =

    0.6275

>> Q2=quad(fun,0,2)

Q2 =

    0.6275

% 梯形法
>> m=pi/20;
>> x=0:m:pi/2;
>> y=cos(x);
>> z=trapz(y)*m

z =

    0.9979

% 自适应辛普森积分法
>> z=quad('cos',0,pi/2)

z =

    1.0000

10.4.3 全局自适应积分法

q=integral(fun,xmin,xmax) % 在xmin~xmax间以数值形式对函数fun求积分
g=integral(fun,xmin,xmax,Name,Value) % 指定一个或多个Name，Value参数对
g=integral2(fun,xmin,xmax,ymin,ymax)
q=integral2(fun,xmin,xmax,ymin,ymax,Name,Value)
q=integral3（fun,xmin,xmax,ymin,ymax,zmin,zmax)
q=integral3（fun,xmin,xmax,ymin,ymax,zmin,zmax,Name,Value)

>> fun=@(x) exp(-x.^2).*log(x).^2; % 创建匿名函数
>> q=integral(fun,0,Inf) % 求积分

q =

    1.9475

>> fun=@(x,y,z) x.*cos(y)+x.^2.*cos(z); % 创建匿名函数
>> xmin=-1; xmax=1;
>> ymin=@(x) -sqrt(1-x.^2); ymax=@(x) sqrt(1-x.^2);
>> zmin=@(x,y) -sqrt(1-x.^2-y.^2); zmax=@(x,y) sqrt(1-x.^2-y.^2);
>> q=integral3(fun,xmin,xmax,ymin,ymax,zmin,zmax)

q =

    0.7796

10.5 常微分方程（组）的数值求解

函数	求解问题类型	方法
ode23	求解非刚性微分方程—低阶方法	显式Runge-Kutta(2,3)法
ode45	求解非刚性微分方程—中阶方法	基于显式Runge-Kutta(4,5)的Dormand-Prince法
ode113	求解非刚性微分方程—变阶方法	Adams-Bashforth-Moulton PECE求解
ode78	求解非刚性微分方程—高阶方法	7阶连续外推Runge-Kutta 8(7)法
ode89	求解非刚性微分方程—高阶方法	8阶连续外推Runge-Kutta 9(8)法
ode15s	求解刚性微分方程和DAE—变阶方法	基于1到5阶数值微分公式(NDF)的VSVO求解器
ode23s	求解刚性微分方程—低阶方法	改进的二阶Rosenbrock法
ode23t	求解中等刚性的ODE和DAE—梯形法	使用“自由”插值的梯形法
ode23tb	求解刚性微分方程—梯形法+后向差分公式	TR-BDF2，采用隐式Runge-Kutta公式
ode15i	求解全隐式微分方程—变阶方法	基于1到5阶后向差分公式(BDF)的VSVO求解器

[X,Y]=odeN('odex',[t0,tf],y0,tol,trace)

新建“函数 odex1.m 文件”

function dy=odex1(x,y)
    dy=[y(2);y(3);y(2)*(1+y(3)^2)-y(1)];
end

>> [X,Y]=ode45('odex1',[0 30],[1;-1;0]); % 调用ode45命令求解
警告: 在 t=9.144275e-01 处失败。在时间 t 处，步长必须降至所允许的最小值(1.776357e-15)以下，才能达到积分容差要求。 
> 位置：ode45 (第 346 行)

>> plot(X,Y(:,1),'r-',X,Y(:,2),'k:',X,Y(:,3),'b--') % 绘图并观察变化趋势
>> xlabel('timeX');
>> ylabel('solutionY');
>> legend('Y1','Y2','Y3');

>> [X,Y]=ode45('odex1',[0 0.9],[1;-1;0]);
>> plot(X,Y(:,1),'r-',X,Y(:,2),'k:',X,Y(:,3),'b--')
>> xlabel('timeX');
>> ylabel('solutionY');
>> legend('Y1','Y2','Y3');

新建“函数 rigid.m 文件”

function dy=rigid(t,y)
    dy=zeros(3,1); % 列向量
    dy(1)=-y(2)*y(3);
    dy(2)=y(1)*y(3);
    dy(3)=2*y(1)*y(2);
end

>> options=odeset('RelTol',1e-4,'AbsTol',[1e-4 1e-4 1e-5]);
>> [t,Y]=ode45(@rigid,[0 12],[1 0 1],options); % 调用ode45命令求解
>> plot(t,Y(:,1),'-',t,Y(:,2),'-.',t,Y(:,3),'.') % 绘图并观察变化趋势

新建“函数 vdp.m 文件”

function dy=vdp(t,y)
    dy=zeros(2,1); % 列向量
    dy(1)=y(2);
    dy(2)=900*(1-y(1)^2)*y(2)-y(1);
end

>> [T,Y]=ode15s(@vdp,[0 4000],[2 0]); % 调用ode15s命令求解
>> plot(T,Y(:,1),'-o') % 绘图并观察变化趋势

10.6 数据分析

函数名	功能描述	基本调用格式
max	求最大值	C=max(A)	如果A是向量，则返回向量中的最大值；如果A是矩阵，则返回一个包含各列最大值的行向量
		C=max(A,B)	返回矩阵A和B中较大的元素，矩阵A、B必须具有相同的大小
		C=max(A,[],dim)	返回dim维上的最大值[C,1]=max(...)，多返回最大值的下标
min	求最小值	与求最大值函数max的调用格式一致
mean	求平均值	M=mean(A)	如果A是向量，则返回向量A的平均值；如果A是矩阵，则返回含有各列平均值的行向量
mean	求平均值	M=mean(A,dim)	返回dim维上的平均值
median	求中间值	与求平均值函数mean的调用格式一致
std	求标准方差	s=std(A)	如果A是向量，则返回向量的标准方差；如果A是矩阵，则返回含有各列标准方差的行向量
		s=std(A,flag)	用flag选择标准方差的定义式
		s=std(A,flag,dim)	返回dim维上的标准方差
var	方差（标准方差的平方）	var(A)	如果A是向量，则返回向量的方差；如果A是矩阵，则返回含有各列方差的行向量
		var(A,1)	返回第二种定义的方差
		var(A,w)	利用w作为权重计算方差
		var(A,w,dim)	返回dim维上的方差
sort	数据排序	B=sort(A)	如果A是向量，则升序排列向量；如果A是矩阵，则升序排列各列
		B=sort(A,dim)	升序排列矩阵A的dim维
		B=sort(...,mode)	用mode选择排序方式：ascend为升序，descend为降序
		[B,IX]=sort(...)	多返回数据B在原来矩阵中的下标IX
sortrows	对矩阵的行排序	B=sortrows(A)	升序排序矩阵A的行
		B=sortrows(A,column)	以column列数据作为标准，升序排序矩阵A的行
		[B,index]=sortrows(A)	多返回数据B在原来矩阵A中的下标index
sum	求元素之和	B=sum(A)	如果A是向量，则返回向量A的各元素之和；如果A是矩阵，则返回含有各列元素之和的行向量
		B=sum(A,dim)	求dim维上的矩阵元素之和
		B=sum(A,'double')	返回数据类型指定为双精度浮点数
		B=sum(A,'native')	返回数据类型指定为与矩阵A的数据类型相同
prod	求元素的连乘积	B=prod(A)	如果A是向量，则返回向量A的各元素的连乘积；如果A是矩阵，则返回含有各列元素连乘积的行向量
		B=prod(A,'all')	返回A的所有元素的乘积
		B=prod(A,dim)	返回dim维上的矩阵元素连乘积
hist	画直方图	n=hist(Y)	在10个等间距的区间内统计矩阵Y属于该区间的元素个数
		n=hist(Y,x)	在x指定的区间内统计矩阵Y属于该区间的元素个数
		n=hist(Y,nbins)	用nbins个等间距的区间统计矩阵Y属于该区间的元素个数
		hist(...)	直接画出直方图
histc	直方图统计	n=histc(x,edges)	计算在edges区间内向量x属于该区间的元素个数
histc	直方图统计	n=histc(x,edges,dim)	在dim维上统计x出现的次数
trapz	梯形数值积分（等间距）	Z=trapz(Y)	返回Y的梯形数值积分
		Z=trapz(X,Y)	计算以X为自变量时Y的梯形数值积分
		Z=trapz(...,dim)	在dim维上计算梯形数值积分
cumsum	矩阵的累加	B=cumsum(A)	如果A是向量，则计算向量A的累加和；如果A是矩阵，则计算矩阵A在列方向上的累加和
cumsum	矩阵的累加	B=cumsum(A,dim)	在dim维上计算矩阵A的累加和
cumprod	矩阵的累积	与函数cumsum的调用格式相同
cumtrapz	梯形积分累积	与函数trapz的调用格式相同

10.6.1 最大值、最小值、平均值、中间值、元素求和

>> x=1:20;
>> y=randn(1,20); % 创建20个随机数y
>> plot(x,y); hold on;
>> [y_max,I_max]=max(y);
>> plot(x(I_max),y_max,'*');
>> [y_min,I_min]=min(y);
>> plot(x(I_min),y_min,'o');
>> y_mean=mean(y);
>> plot(x,y_mean*ones(1,length(x)),'--');
>> legend('数据','最大值','最小值','平均值');

10.6.2 标准差和方差

>> x1=rand(1,200);
>> x2=8*x1;
>> std_x1=std(x1);
>> var_x1=var(x1);
>> std_x2=std(x2);
>> var_x2=var(x2);
>> disp(['x2的标准方差与x1的标准方差之比=',num2str(std_x2/std_x1)]);
x2的标准方差与x1的标准方差之比=8
>> disp(['x2的方差与x1的方差之比=',num2str(var_x2/var_x1)]);
x2的方差与x1的方差之比=64

10.6.3 元素排序

>> a=[0 -13i 1 i -i -3i 3 -3];
>> b=sort(a)

b =

   0.0000 + 0.0000i   0.0000 - 1.0000i   1.0000 + 0.0000i   0.0000 + 1.0000i   0.0000 - 3.0000i   3.0000 + 0.0000i  -3.0000 + 0.0000i   0.0000 -13.0000i

10.7 多项式函数

10.7.1 多项式表示法

>> poly2sym([1 -2 0 8 0 6 -8])
 
ans =
 
x^6 - 2*x^5 + 8*x^3 + 6*x - 8

10.7.2 多项式求值

y=polyval(p,x)

Y=polyvalm(p,X) % 把矩阵X代入多项式p中进行计算，矩阵X必须是方阵

>> p1=[1 3 6]; % 多项式x^2+3x+6的系数
>> A=[10 -1];
>> A1=[1 0; 0 1];
>> p1_A=polyval(p1,A) % 求多项式的值

p1_A =

   136     4

>> p1_Am=polyvalm(p1,A1) % 求矩阵多项式的值

p1_Am =

    10     0
     0    10

函数名	功能描述	函数名	功能描述	函数名	功能描述
poly	求多项式的系数	roots	求多项式的根	deconv	去卷积或多项式除法
polyeig	求多项式特征值问题	polyval	求多项式的值	polyint	求多项式的积分
polyfit	多项式曲线拟合	polyvalm	求矩阵多项式的值	polyder	求多项式的一阶导数（微分）
residue	部分分式展开（分解）	conv	卷积或多项式乘法	...	...

posted @ 2026-01-12 10:43 Zhuye_inking 阅读(37) 评论(0) 收藏举报

刷新页面返回顶部

inking

第10章 数值计算

第10章 数值计算

10.1 线性方程组的解法

10.1.1 直接解法

10.1.2 逆矩阵法

10.1.3 利用矩阵的LU分解求解

10.1.4 求线性方程组的其他解法

10.1.4.1 Jacobi迭代法

10.1.4.2 Gauss-Seidel迭代法

10.2 插值

10.2.1 一维数据插值

10.2.2 二维数据插值

10.2.3 三维及多维数据插值

10.2.4 三次样条数据插值

10.2.5 快速傅里叶变换插值

10.2.6 对二维或三维散点数据插值

10.3 曲线拟合

10.4 数值积分

10.4.1 梯形法数值积分

10.4.2 自适应辛普森积分法

10.4.3 全局自适应积分法

10.5 常微分方程（组）的数值求解

10.6 数据分析

10.6.1 最大值、最小值、平均值、中间值、元素求和

10.6.2 标准差和方差

10.6.3 元素排序

10.7 多项式函数

10.7.1 多项式表示法

10.7.2 多项式求值

公告

第10章数值计算

第10章数值计算