第6章数据可视化

6.1 绘图基础

6.1.1 离散数据的可视化

\[用图形表示离散函数y=\dfrac{100}{|(n-12)(n+20)|},n=0,1,\cdots,50。 \]

>> n=0:50; % 取51个点
>> y=100./abs((n-12).*(n+20)); % 准备离散数据点
>> plot(n,y,'.','MarkerSize',16); % 绘制散点图
>> grid % 添加栅格

6.1.2 连续函数的可视化

>> x=linspace(0,2*pi,21); % 在0~2π间取21个点，作为自变量x
>> y=sin(x); % 对应sin的函数值y
>> plot(x,y,'-o'); % 绘制图形
>> grid % 添加栅格

6.1.3 数据可视化的通用步骤

步骤	内容	典型命令示例
1	准备数据。选定所要绘图的范围，产生自变量采样向量，并计算相应的函数值	x=linspace(0,2*pi,21); % 自变量x y=sin(x); % 因变量y
2	选定图形窗口及子图位置。默认打开Figure1，或当前窗口，或当前子图：通过命令可以指定图形窗口和子图位置	figure(1);subplot(2,3,2) figure(1);subplot(2,3,5)
3	调用绘图命令，可指定线型、线宽、颜色、数据点类型等	plot(x,y,'r-*')
4	设置轴的范围与刻度、坐标栅格	axis([0,2*pi,-1.2,1.2]) % 坐标轴范围 grid on % 栅格控制
5	添加图形注释。包括图题、轴题、图例、文字说明等	title(figure) % 图题 xlabel(x);ylabel(y) % 轴题 legend(x,sin(x)) % 图例 text(2,0.5,y=sin(x) % 说明
6	图形精细修饰。利用对象属性值及图形窗口工具栏进行设置	set(h,MarkerSize,8) % 设置数据点大小
7	导出与打印图形	无命令，采用图形窗口菜单操作

6.2 二维图形的绘制

6.2.1 plot绘图命令

plot(y) % 绘制y对一组隐式x坐标的图
plot(x,y) % 绘制y中数据对x中对应值的二维线图
plot(x1,y1,...,xn,yn) % 在同一组坐标轴上绘制多对x和y坐标
plot(___,LineSpec) % 使用指定的线型、标记和颜色绘图
plot(___,Name,Value) % 使用一个或多个名称—值参数对指定线条属性

其中，Name，Value为名称—值参数对，Name可以为‘Marker’（标记）、‘MarkerFaceColor’（标记颜色），‘LineStyle’（线型），‘LineWidth’（线宽）等。设置格式为

'Marker','o','MarkerFaceColor','r'

6.2.1.1 plot(y)命令

>> x=0:pi/5:4*pi;
>> y=2*cos(x);
>> plot(y) % 绘制的向量曲线，x坐标从1至length(y)

>> y=[3 6 9; 2 4 6; 1 2 3]; % 创建实数矩阵
>> plot(y) % 绘制矩阵曲线，即绘制y中各列对其行号的图，x坐标为从1到y的行数

>> x=[1:0.5:10];
>> y=[1:0.5:10];
>> z=x+sin(y).*i; % 创建复数向量
>> plot(z) % 绘制的复数向量曲线，实部为横坐标、虚部为纵坐标

6.2.1.2 plot(x,y)命令

>> x=0:pi/10:4*pi;
>> y=2*sin(x);
>> plot(x,y) % 绘制的双向量曲线

>> x=0:pi/10:4*pi;
>> y=[sin(1.5*x); cos(x)+2];
>> plot(x,y) % 绘制的向量和矩阵曲线

>> x=[1 2 3; 4 5 6; 7 8 9];
>> y=[7 8 9; 6 5 4; 1 2 3];
>> plot(x,y) % 绘制的双矩阵曲线

% plot(x,y1,x,y2,x,y3,...)以公共向量x为横轴，分别以y1、y2、y3、...为纵轴，其效果与双矩阵曲线的绘制效果类似。

6.2.1.3 plot(x,y,LineSpec)命令

标记符号	标记	颜色符号	颜色	线型符号	线型
'.'	点	'r'	红色	'-'	实线（默认）
'o'	圆圈	'g'	绿色	'--'	虚线
'+'	加号	'b'	蓝色	'-.'	点画线
'**'	星号	'c'	青色	':'	点线
'x'	叉号	'm'	紫色	'none'	无线条
's'	方形	'y'	黄色
'd'	菱形	'w'	白色
'^'	上三角	'k'	黑色
'v'	下三角
'>'	右三角
'<'	左三角
'p'	五角形
'h'	六角形
'_'	水平线条—
'\|'	数值线条\|
'none'	无标记

>> x=0:pi/50:4*pi;
>> y=sin(x);
>> plot(x,y,'k.')

>> x=0:pi/20:6*pi;
>> y1=sin(x);
>> y2=cos(x);
>> plot(x,y1,'k-',x,y2,'r--') % 绘制不同颜色和线型的曲线

>> t=(0:pi/100:2*pi)';
>> y1=sin(t)*[1,-1];
>> y2=sin(t).*cos(6*t);
>> t3=2*pi*(0:10)/10;
>> y3=sin(t3).*sin(10*t3);
>> plot(t,y1,'r:',t,y2,'-bo',t3,y3,'m.') % y=sin(t)cos(t)的图形包络线

6.2.2 绘制双坐标图

6.2.2.1 plotyy函数

plotyy(X1,Y1,X2,Y2) % 绘制Y1对X1的图，在左侧显示y轴标签；同时绘制Y2对X2的图，在右侧显示y轴标签
plotyy(X1,Y1,X2,Y2,function) % 使用指定的绘图函数生成图形
plotyy(X1,Y1,X2,Y2,'function1','function2') % 使用function1(X1,Y1)绘制左轴的数据；使用function2(X2,Y2)绘制右轴的数据

其中，function可以是指定plot、semilogx、semilogy、loglog、stem的函数句柄或字符向量，或者是能接受一下以下语法的任意MATLAB函数：

h=function(x,y)

plotyy(x1,y1,x2,y2,@loglog) % 函数句柄
plotyy(x1,y1,x2,y2,'loglog') % 字符向量

>> x=0:0.01:20;
>> y1=200*exp(-0.05*x).*sin(x);
>> y2=0.8*exp(-0.5*x).*sin(10*x);
>> plotyy(x,y1,x,y2) % 绘制双y轴图

6.2.2.2 使用yyaxis命令

yyaxis left % 激活当前坐标区中与左侧y轴关联的一侧，后续图形命令的目标为左侧
yyaxis right % 激活当前坐标区中与右侧y轴关联的一侧，后续图形命令的目标为右侧

>> x=linspace(0,10);
>> y=sin(3*x);
>> yyaxis left % 激活左轴
>> plot(x,y)
>> z=sin(3*x).*exp(0.5*x);
>> yyaxis right % 激活右轴
>> plot(x,z)
>> ylim([-150 150]) % 绘制双y轴图

6.2.2.3 fplot绘图命令

fplot(f) % 在默认区间[-5,5]（对x）绘制函数y=f(x)定义的曲线
fplot(f,xinterval) % 在指定区间[xmin,xmax]内绘图
fplot(funx,funy) % 在默认区间[-5,5]（对t）绘制由x=funx(t)与y=funy(t)定义的曲线
fplot(funx,funy,tinterval) % 在指定区间[tmin,tmax]内绘图
fplot(___,LineSpec) % 指定线型、标记符号和线条颜色
fplot(___,Name,Value) % 使用一个或多个名称—值参数对指定线条属性

>> ff=@tan;
>> fplot(ff,[-3 6]); % 在指定区间内绘图

>> xt=@(t)cos(3*t);
>> yt=@(t)sin(2*t);
>> fplot(xt,yt) % 绘制参数化曲线x=cos(3t)和y=sin(2t)

6.2.2.4 ezplot绘图函数

ezplot(f) % 在默认区间[-2π 2π]（对x）绘制y=f(x)定义的曲线
ezplot(f,xyinterval) % 在指定区间[min,max]绘图
ezplot(f2) % 在默认区间[-2π 2π]（对x和y）绘制f2(x,y)=0定义的曲线
ezplot(f2,xyinterval) % 在指定区间[xmin,xmax,ymin,ymax]绘制图
ezplot(funx,funy) % 在默认区域[0 2π]（对u）绘制x=funx(u)和y=funy(u)通过参数方式定义的平面曲线
ezplot(funx,funy,xyinterval) % 在指定区间[umin,umax]绘图

>> ezplot('x^4-y^6')

6.2.2.5 多次叠图操作

>> x=linspace(0,4*pi,50);
>> y=sin(x);
>> z=cos(x);
>> plot(x,y,'b');
>> hold on;
>> plot(x,z,'k--');
>> legend('sin(x)','cos(x)'); % 添加标签
>> hold off

6.2.2.5 多子图操作

>> x=linspace(0,4*pi,40);
>> y=sin(x);
>> z=cos(x);
>> t=sin(x)./(cos(x)+eps);
>> ct=cos(x)./(sin(x)+eps);

>> subplot(2,2,1); plot(x,y);
>> title('sin(x)');
>> subplot(2,2,2); plot(x,z);
>> title('cos(x)');
>> subplot(2,2,3); plot(x,t);
>> title('tangent(x)');
>> subplot(2,2,4); plot(x,ct);
>> title('cotangent(x)');

6.3 三维图形的绘制

6.3.1 plot3绘图命令

plot3(X,Y,Z) % 绘制三维空间中的坐标，X、Y、Z为向量或矩阵
plot3(X,Y,Z,LineSpec) % 使用LineSpec指定的线型、标记和颜色绘图
plot3(X1,Y1,Z1,...,Xn,Yn,Zn) % 在同一组坐标轴上绘制多组坐标
plot3(X1,Y1,Z1,LineSpec1,...,Xn,Yn,Zn,LineSpecn) % 为每个XYZ三元组指定特定的线型、标记和颜色

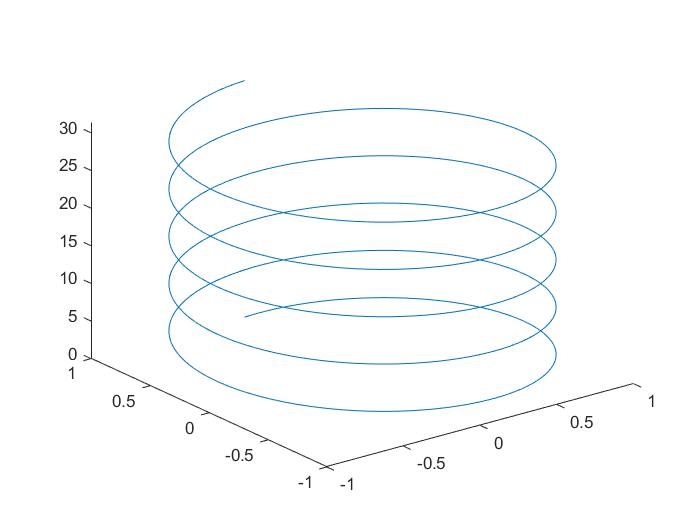
>> t=0:pi/50:10*pi;
>> plot3(sin(t),cos(t),t) % 绘制螺旋线

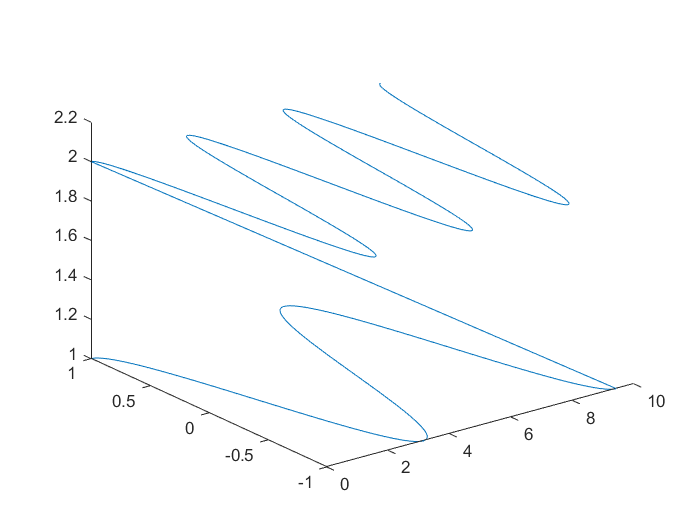
>> t=0:pi/100:3*pi;
>> x=[t t];
>> y=[cos(t) cos(2*t)];
>> z=[(sin(t)).^2+(cos(t)).^2 (sin(t)).^2+(cos(t)).^2+1];
>> plot3(x,y,z) % 绘制矩阵向量曲线

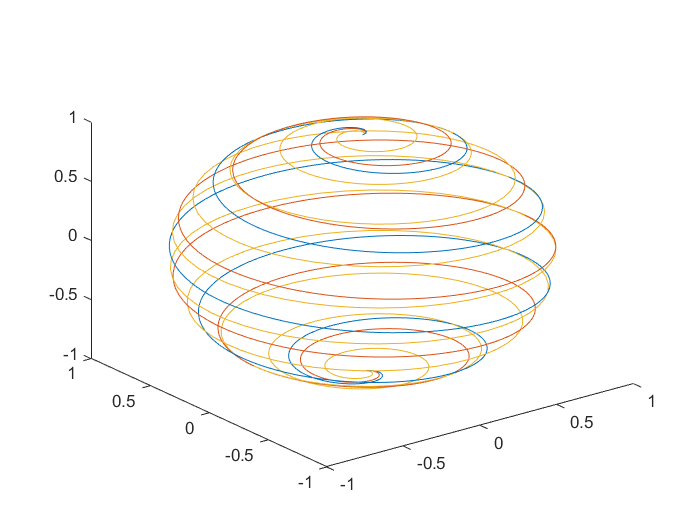
>> t=0:pi/500:pi;
>> X=[sin(t).*cos(10*t); sin(t).*cos(12*t); sin(t).*cos(20*t);];
>> Y=[sin(t).*sin(10*t); sin(t).*sin(12*t); sin(t).*sin(20*t);];
>> Z=cos(t); % 创建矩阵Z，其中包含所有三组坐标的z坐标
>> plot3(X,Y,Z) % 在同一坐标轴上绘制三组曲线

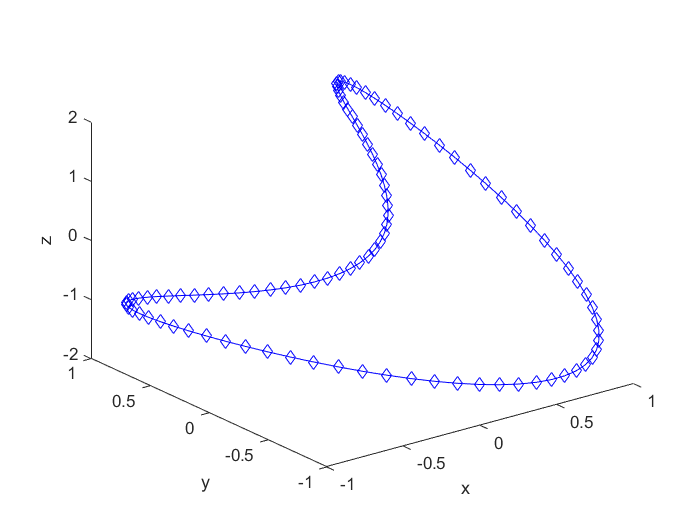
>> t=(0:0.02:2)*pi;
>> x=sin(t);
>> y=sin(2*t);
>> z=2*cos(t);
>> plot3(x,y,z,'b-',x,y,z,'bd') % 通过三维曲线图演示该曲线的参数方程
>> xlabel('x'),ylabel('y'),zlabel('z')

6.3.2 三维网格图和三维曲面图的绘制

6.3.2.1 三维网格图mesh命令

mesh(X,Y,Z) % 创建一个网格图，该网格图为三位曲面，有实色边颜色，无面颜色
mesh(Z) % 创建一个网格图，并将Z中元素的列索引和行索引用作x坐标和y坐标
mesh(___,C) % 进一步指定边的颜色

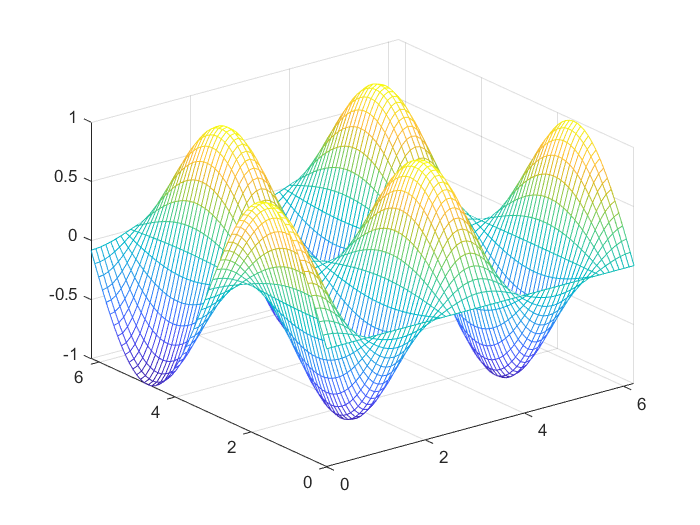
>> x=0:0.1:2*pi;
>> y=0:0.1:2*pi;
>> z=sin(x').*cos(2*y);
>> mesh(x,y,z) % 绘制三维网格图

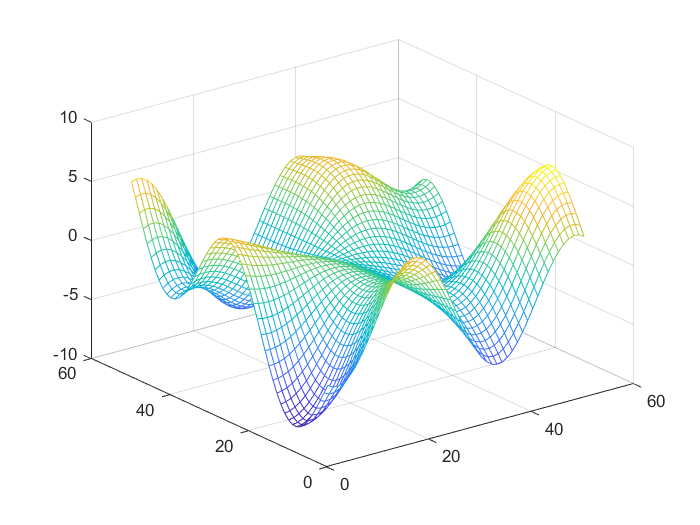
>> [X,Y]=meshgrid(-5:.2:5);
>> Z=Y.*sin(X)-X.*cos(Y);
>> mesh(Z) % 绘制三维网格图

6.3.2.2 三维曲面图surf命令

surf(X,Y,Z) % 创建一个具有实色边和实色面的三维曲面
surf(Z) % 创建一个曲面图，并将Z中元素的列索引和行索引用作x坐标和y坐标
surf(___,C) % 通过C指定曲面的颜色

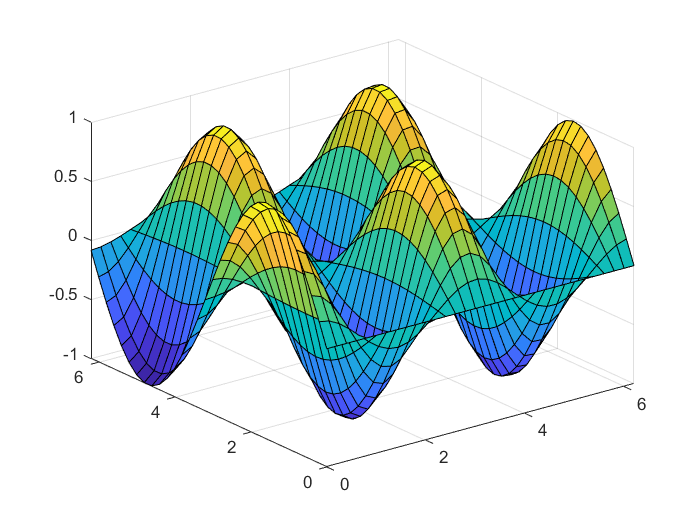
>> x=0:0.2:2*pi;
>> y=0:0.2:2*pi;
>> z=sin(x')*cos(2*y);
>> surf(x,y,z)

6.3.3 其他三位绘图函数

6.3.3.1 meshgrid、meshc和meshz

[X,Y]=meshgrid(x,y)

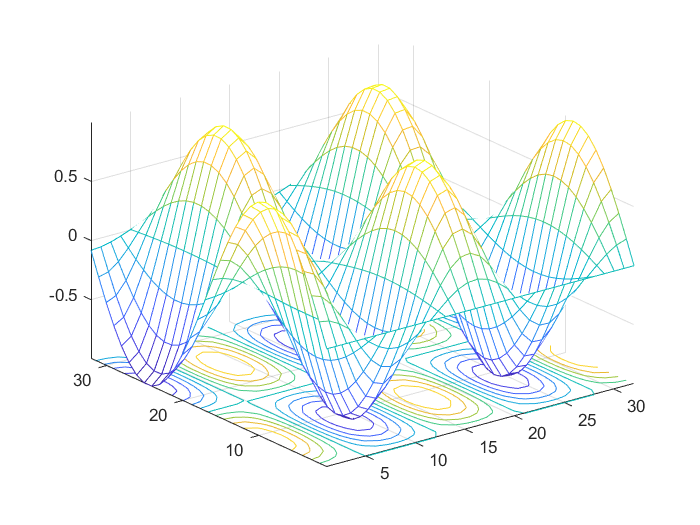
>> x=0:0.2:2*pi;
>> y=0:0.2:2*pi;
>> z=sin(x')*cos(2*y);
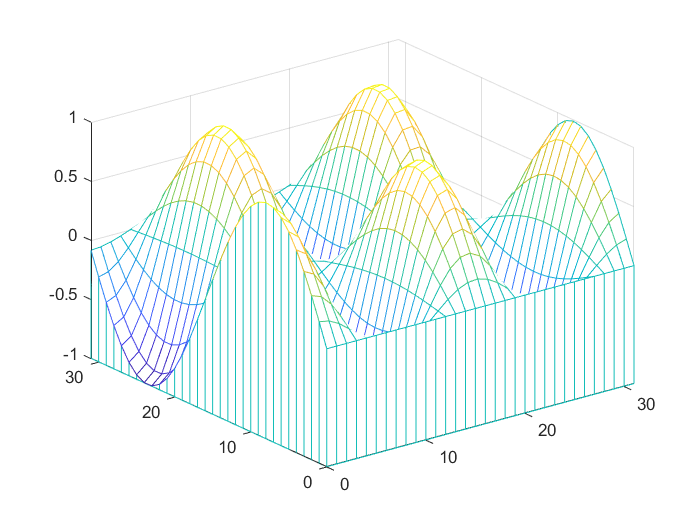
>> meshc(z) % 利用meshc命令绘制三维网格图
>> meshz(z) % 利用meshz命令绘制三维网格图

6.3.3.2 surfc和surfl命令

surfl(Z) % 创建曲面，并将Z中的元素的列索引和行索引作为x坐标和y坐标
surfl(X,Y,Z) % 创建一个带光源高光的三维曲面图，X、Y、Z定义x、y、z的坐标
surfl(___,S) % 参数S为一个三维向量[Sx,Sy,Sz]，用于指定光源的方向
surfl(X,Y,Z,S,K) % K为反射常量

>> x=0:0.2:2*pi;
>> y=0:0.2:2*pi;
>> z=sin(x')*cos(2*y);
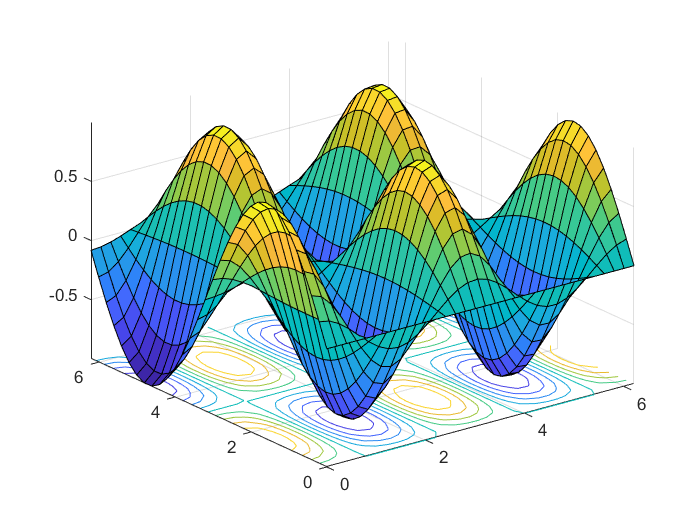
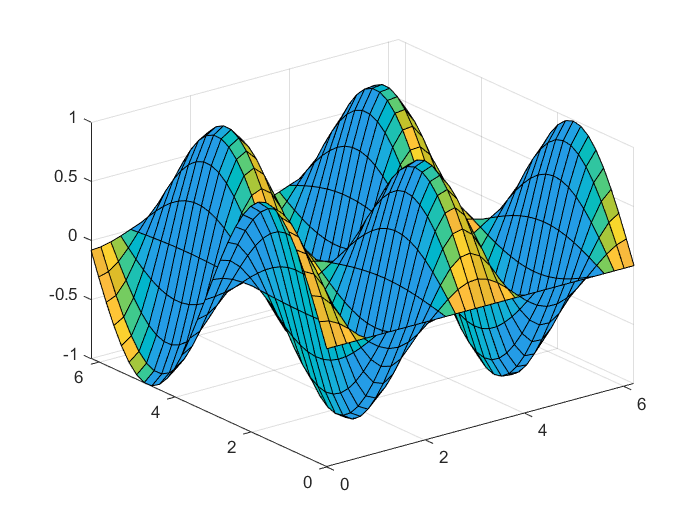
>> surfc(x,y,z) % 绘制等高线三维曲面图
>> surfl(x,y,z) % 绘制光照效果三维曲面图

6.4 特殊图形的绘制

6.4.1 二维特殊图形函数

函数名	说明	函数名	说明	函数名	说明
pie	饼状图	gplot	拓扑图	hist/histogram	二维条形直方图
area	填充绘图	quiver	向量场	scatter	散射图
comat	彗星图	contour	等高线图	stem	离散数据序列针状图
errorbar	误差条图	barh	水平条形图	stairs	阶梯图
feather	矢量图	bar	垂直条形图	rose	极坐标系下的柱状图
fill	多边形填充	plotmatrix	分散矩阵绘制	...	...

6.4.1.1 pie命令

pie(X) % 使用X中的数据绘制饼状图，饼状图中的每个扇区代表X中的一个元素
pie(X,explode) % 指定扇区从饼状图偏移一定位置
pie(X,labels) % 指定扇区的文本标签，X是数值型，标签数必须等于X中的元素数
pie(X,explode,labels) % 偏移扇区并指定文本标签，X可以是数值或分类数据类型

>> x=[0.43 .30 .68 .45 .8];
>> pie(x)
>> y=[0 0 0 1 0];
>> pie(x,y)

6.4.1.2 stairs命令

stairs(Y) % 绘制Y中元素的阶梯图，Y为向量时，绘制一条线条；Y为矩阵时，为每个矩阵列绘制一条线条
stairs(X,Y) % 在Y中由X指定的位置绘制元素，X和Y必须是相同大小的向量或矩阵，X可以是行向量或列向量，Y必须是包含length(X)行的矩阵
stairs(___,LineSpec) % LineSpec指定线型、标记和颜色

>> X=linspace(0,4*pi,40); % 在[0,4π]区间取40个均匀分布的值
>> Y=sin(X);
>> stairs(Y) % 创建阶梯图，Y的长度自动确定并生成x轴刻度
>> stairs(X,Y) % 在指定的x值位置绘制单个数据序列阶梯图

6.4.1.3 bar与barh命令

bar(y) % 创建一个条形图，y中的每个元素对应一个条形。若y是m*n的矩阵，则创建每组包含n个条形的m个组
bar(x,y) % 在x指定的位置绘制条形图
bar(___,width) % 设置条形的相对宽度以控制组中各个条形的间隔
bar(___,style) % 指定条形组样式，包括'grouped'（默认）|'stacked'|'hist'|'histc'
bar(___,color) % 设置条形的颜色，包括'b'|'r'|'g'|'c'|'m'|'y'|'k'|'w'

>> x=-2.5:0.25:2.5;
>> y=2*exp(-x.*x);
>> bar(x,y,'b') % 绘制条形图
>> y=[2 2 3; 2 5 6; 2 8 9; 2 11 12];
>> bar(y) % 显示4个条形组，每组包含3个条形

>> X=round(20*rand(3,4));
>> subplot(2,2,1); bar(X,'group'); title('bargroup')
>> subplot(2,2,2); barh(X,'stack'); title('barhstack')
>> subplot(2,2,3); bar(X,'stack'); title('barstack')
>> subplot(2,2,4); bar(X,1.2); title('barwidth=1.2')

6.4.1.4 hist/histogram命令

hist(y) % 把向量y中的元素放入等距的10个条形中，且返回每个条形中的元素个数，若y为矩阵，则该命令按列对y进行处理
hist(y,x) % 参量x为标量，用于指定条形的数目；参量x为向量，把y中的元素放到m（m=length(x)）个由x中的元素指定的位置为中心的条形中
histogram(x) % 基于X使用自动分组划分算法创建直方图。矩形高度为各分组元素数量
histogram(X,nbins) % 使用标量nbins指定的分组数量
histogram(X,edges) % 将X划分到由向量edges指定边界的分组内

>> x=-2.5:0.25:2.5;
>> y=randn(5000,1);
>> hist(y,x)

>> x=randn(1000,1);
>> nbins=25;
>> histogram(x,nbins) % 根据等距分组的随机数绘制条形直方图

6.4.1.5 stem命令

stem(Y) % 将数据序列Y绘制为从x轴的基线延伸的针状图，数据值由终止于每个针状图的圆表示
stem(X,Y) % 在X指定值的位置绘制数据序列Y。X、Y必须是大小相同的向量或矩阵

>> Y=linspace(-2*pi,2*pi,20); % 创建一个在[-2π,2π]区间内的20个离散数据值
>> stem(Y) % 绘制离散数据序列针状图

>> X=linspace(0,2*pi,20); % 在[0,2π]区间内产生20个余弦数据值
>> Y=cos(X);
>> stem(X,Y) % 绘制离散数据序列针状图

6.4.1.6 contour命令

contour(Z) % 创建一个包含矩阵Z的等高线图，其中Z包含XY平面上的高度值，Z的列索引和行索引分别是平面中的X和Y坐标
contour(X,Y,Z) % 指定Z中各值的X和Y坐标
contour(___,levels) % 为等高线指定最后一个参数
contour(___,LineSpec) % 指定等高线的线型和颜色

>> [X,Y]=meshgrid(-2:.2:2,-2:.2:3);
>> Z=2*Y.*exp(-X.^2-Y.^2);
>> contour(X,Y,Z);

>> [X,Y,Z]=peaks; % 调用peaks函数以创建x、Y和Z
>> contour(X,Y,Z,20) % 绘制Z的20条等高线

6.4.1.7 quiver命令

quiver(u,v) % 在XY平面的等距点处绘制u和v指定的向量
quiver(x,y,u,v) % 在坐标(x,y)处用箭头图形绘制向量，(u,v)为相应点的速度分量，x、y、u、v必须大小相同
quiver(___,scale) % scale用来控制图中向量长度的实数，默认为1

>> [X,Y]=meshgrid(-2:.2:2,-2:.2:3);
>> Z=2*Y.*exp(-X.^2-Y.^2);
>> [DX,DY]=gradient(Z,.2,.2);
>> contour(X,Y,Z)
>> hold on
>> quiver(X,Y,DX,DY)

6.4.1.8 errorbar命令

errorbar(y,err) % 创建y中的数据线图，并在每个数据点处绘制一个垂直误差条，err中的值确定数据点上方和下方的每个误差条的长度
errorbar(x,y,err) % 绘制y对x的图，并在每个数据点处绘制一个垂直误差条
errorbar(x,y,neg,pos) % 在每个数据点处绘制一个垂直误差条
errorbar(___,ornt) % ornt设置误差条的方向
errorbar(x,y,yneg,ypos,xneg,xpos) % 绘制y对x的图，并绘制水平和垂直误差条
errorbar(___,linespec) % 设置线型、标记和颜色

>> x=[0:0.1:4*pi];
>> y=2*cos(2*x);
>> e=[0:1/(length(x)-1):1];
>> errorbar(x,y,e)

6.4.1.9 comet命令

comet(y) % 显示向量y的彗星图
comet(x,y) % 显示向量y对向量x的彗星图
comet(x,y,p) % 指定长度为p*1ength(y)的彗星体，p默认为0.1

>> t=0:.01:4*pi;
>> x=sin(t).*(cos(2*t).^2);
>> y=cos(t).*(sin(2*t).^2);
>> comet(x,y);

6.4.2 三维特殊图形函数

函数名	说明	函数名	说明	函数名	说明
bar3	三维条形图	scatter3	三维散射图	trimesh	三角形网格图
comet3	三维慧星轨迹图	quiver3	向量场	sphere	球面图
ezgraph3	函数控制绘制三维图（不推荐）	stem3	三维离散数据图	cylinder	柱面图
pie3	三维饼状图	trisurf	三角形表面图	contour3	三维等高线

6.4.2.1 cylinder命令

[X,Y,Z]=cylinder % 返回半径r=1、高度h=1圆柱体的x、y、z坐标值，不绘图
[X,Y,Z]=cylinder(r) % 返回半径为r、高度h=1圆柱体的x、y、z坐标值，不绘图
[X,Y,Z]=cylinder(r,n) % 额外指定等距点数目n，不绘图
cylinder(___) % 无输出参量时，直接绘制圆柱体

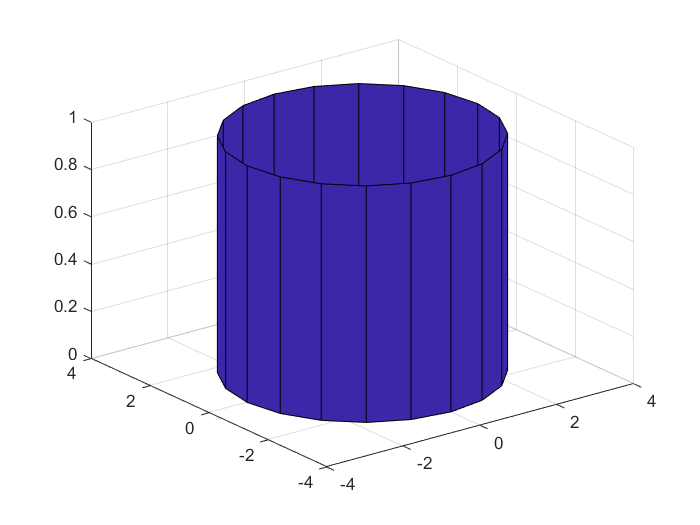
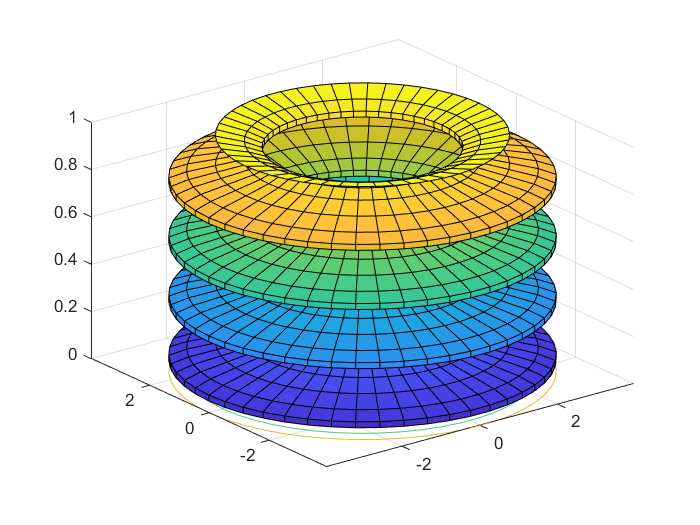
>> cylinder(3) % 绘制圆柱图形

>> t=0:pi/10:4*pi;
>> [X,Y,Z]=cylinder(sin(2*t)+3,50);
>> surfc(X,Y,Z) % 绘制圆柱图形

6.4.2.2 sphere命令

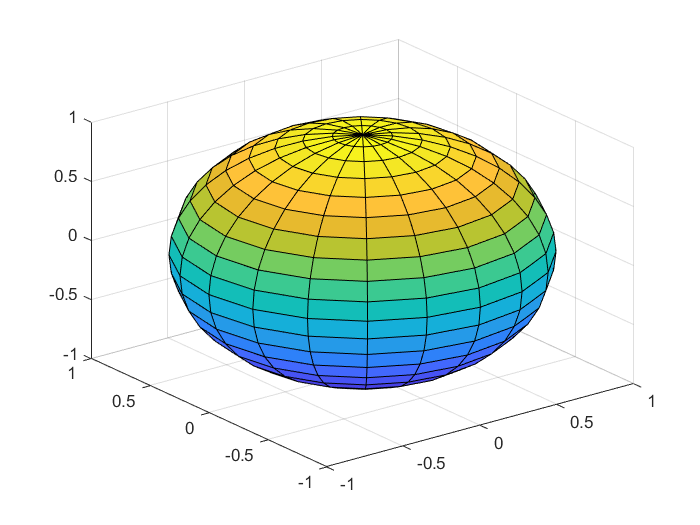
sphere % 生成三维直角坐标系中的单位球体，球体半径为1，由20×20个面组成
sphere(n) % 在当前坐标系中画出有n*n个面的球体
[X,Y,Z]=sphere(___) % 返回3个阶数为(n+1)*(n+1)的直角坐标系中的坐标矩阵

>> sphere % 绘制球体

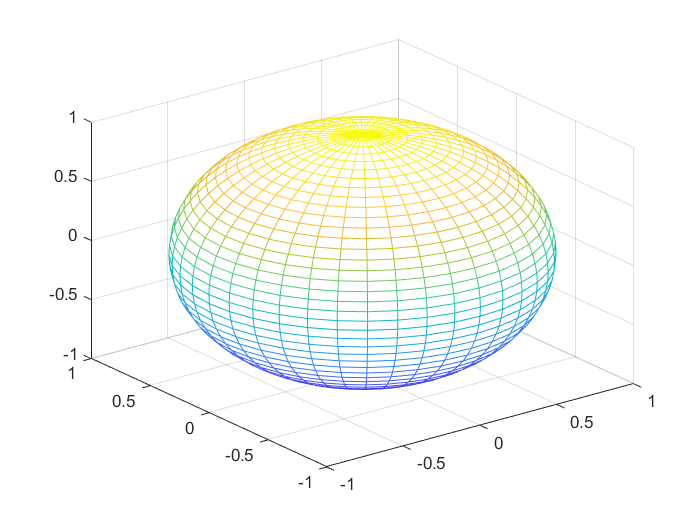
>> [x,y,z]=sphere(40);
>> mesh(x,y,z) % 绘制球体

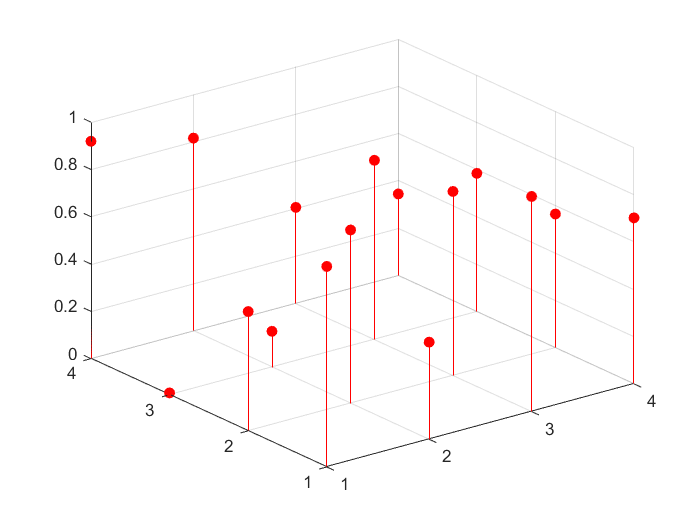
6.4.2.3 stem3命令

stem3(Z) % 将Z中的各项绘制为针状图，从xy平面开始延伸并在各项值处以圆圈终止
stem3(X,Y,Z) % 将Z中的各项绘制为针状图，这些针状图从xy平面开始延伸
stem3(___,'filled') % 填充圆形
stem3(___,LineSpec) % 指定线型、标记和颜色

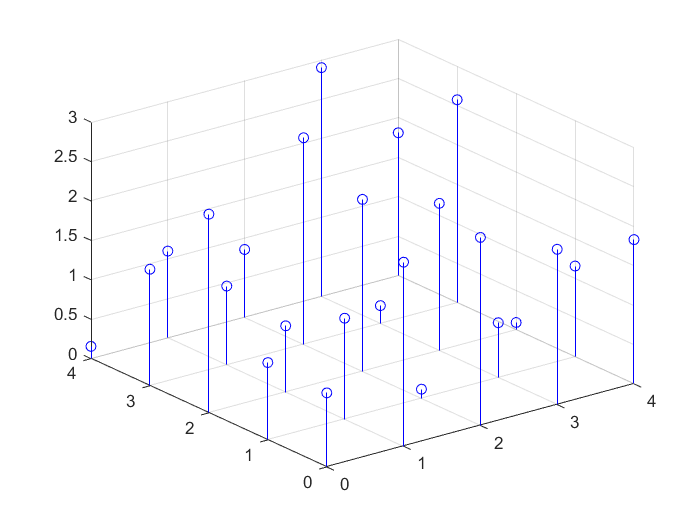
>> x=0:1:4;
>> y=0:1:4;
>> z=3*rand(5);
>> stem3(x,y,z,'bo') % 绘制三维离散数据序列
>> z=rand(4);
>> stem3(z,'ro','filled') % 带填充的三维离散数据序列

6.4.3 特殊坐标轴函数

6.4.3.1 semilogx命令

semilogx(Y) % 对x轴的刻度求常用对数（以10为底），而y轴为线性刻度
semilogx(X1,Y1,X2,Y2,...) % 在同一组坐标轴上绘制多对x和y坐标
semi1ogx(X1,Y1,LS1,X2,Y2,LS2,...) % 按顺序取三参数Xn，Yn，LSn画线

>> x=0:0.01:2*pi;
>> y=abs(100*sin(4*x))+1;
>> plot(x,y); % 绘制图形

>> x=0:0.01:2*pi;
>> y=abs(100*sin(4*x))+1;
>> semilogx(x,y); % 绘制以x轴为对数的坐标图

6.4.3.2 semilogy命令

>> x=0:0.1:4*pi;
>> y=abs(100*sin(2*x))+1;
>> plot(x,y) % 绘制图形

>> x=0:0.1:4*pi;
>> y=abs(100*sin(2*x))+1;
>> semilogy(x,y); % 绘制以y轴为对数的坐标图

6.4.3.3 loglog命令

>> x=0:0.1:2*pi;
>> y=abs(100*sin(3*x))+2;
>> plot(x,y) % 绘制图形

>> x=0:0.1:2*pi;
>> y=abs(100*sin(3*x))+2;
>> loglog(x,y) % 绘制双对数坐标图

6.4.3.4 polar命令

polar(theta,rho) % 创建角theta对半径rho的极坐标图
polar(theta,rho,LineSpec) % LineSpec指定线型、绘图符号及极坐标图中线条颜色

6.4.3.5 polarplot命令

polarplot(theta,rho) % 在极坐标中绘制线条
polarplot(rho) % 按等间距角度（介于0和2π之间）绘制rho中的半径值
polarplot(Z) % 绘制Z中的复数值
polarplot(___,LineSpec) % 设置线条的线型、标记符号和颜色
polarplot(theta1,rho1,...,thetaN,rhoN) % 绘制多个rho，theta对组
polarplot(theta1,rho2,LineSpec1,...,thetaN,rhoN,LineSpecN)

>> theta=0:0.01:2*pi;
>> rho=sin(2*theta).*cos(2*theta);
>> polarplot(theta,rho); % 等同于polar(theta,rho)

6.4.4 四维表现图（三维体切片平面）

slice(V,sx,sy,sz) % 使用V的默认坐标数据绘制切片，切片位置由sx、sy、sz指定
slice(X,Y,Z,V,sx,sy,sz) % 为三维体数据V绘制切片，X、Y和Z作为坐标数据
slice(___,method) % 指定内插值的方法，指定linear、cubic、nearest之一

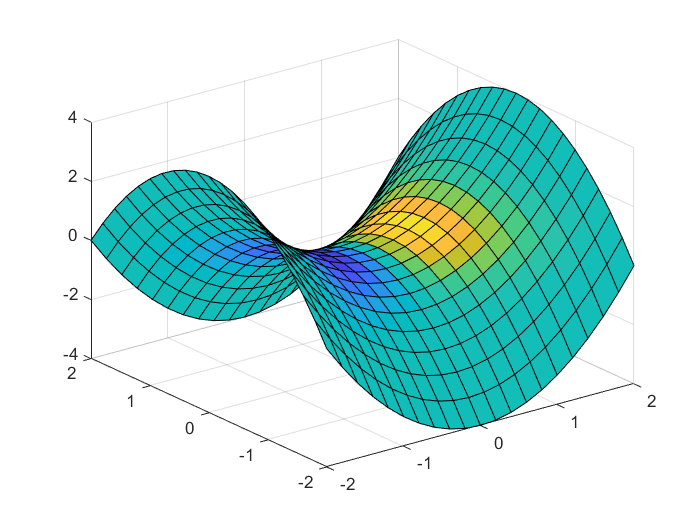
>> [X,Y,Z]=meshgrid(-5:0.2:5);
>> V=X.*exp(-X.^2-Y.^2-Z.^2);
>> [xsurf,ysurf]=meshgrid(-2:0.2:2);
>> zsurf=xsurf.^2-ysurf.^2;
>> slice(X,Y,Z,V,xsurf,ysurf,zsurf) % 绘制切片图

posted @ 2026-01-12 10:02 Zhuye_inking 阅读(0) 评论(0) 收藏举报

刷新页面返回顶部

inking

第6章 数据可视化

第6章 数据可视化

6.1 绘图基础

6.1.1 离散数据的可视化

6.1.2 连续函数的可视化

6.1.3 数据可视化的通用步骤

6.2 二维图形的绘制

6.2.1 plot绘图命令

6.2.1.1 plot(y)命令

6.2.1.2 plot(x,y)命令

6.2.1.3 plot(x,y,LineSpec)命令

6.2.2 绘制双坐标图

6.2.2.1 plotyy函数

6.2.2.2 使用yyaxis命令

6.2.2.3 fplot绘图命令

6.2.2.4 ezplot绘图函数

6.2.2.5 多次叠图操作

6.2.2.5 多子图操作

6.3 三维图形的绘制

6.3.1 plot3绘图命令

6.3.2 三维网格图和三维曲面图的绘制

6.3.2.1 三维网格图mesh命令

6.3.2.2 三维曲面图surf命令

6.3.3 其他三位绘图函数

6.3.3.1 meshgrid、meshc和meshz

6.3.3.2 surfc和surfl命令

6.4 特殊图形的绘制

6.4.1 二维特殊图形函数

6.4.1.1 pie命令

6.4.1.2 stairs命令

6.4.1.3 bar与barh命令

6.4.1.4 hist/histogram命令

6.4.1.5 stem命令

6.4.1.6 contour命令

6.4.1.7 quiver命令

6.4.1.8 errorbar命令

6.4.1.9 comet命令

6.4.2 三维特殊图形函数

6.4.2.1 cylinder命令

6.4.2.2 sphere命令

6.4.2.3 stem3命令

6.4.3 特殊坐标轴函数

6.4.3.1 semilogx命令

6.4.3.2 semilogy命令

6.4.3.3 loglog命令

6.4.3.4 polar命令

6.4.3.5 polarplot命令

6.4.4 四维表现图（三维体切片平面）

公告

第6章数据可视化

第6章数据可视化