第5章矩阵运算

5.1 矩阵分析基础

函数名	功能描述	函数名	功能描述
norm	求矩阵或向量的范数	null	矩阵的零空间
normest	估计矩阵的2阶范数	orth	矩阵的正交化空间
rank	矩阵的秩	rref	矩阵的约化行阶梯形式
det	矩阵的行列式	subspace	求两个矩阵空间之间的夹角
trace	矩阵的迹，即求对角元素的和	...	...

5.1.1 向量的范数

对于线性空间中的一个向量\(\boldsymbol{x}=\{x_1,x_2,\dots,x_n\}\)，如果存在一个函数\(r(\boldsymbol{x})\)满足以下3个条件，则称\(r(\boldsymbol{x})\)为向量\(\boldsymbol{x}\)的范数，一般记为\(\Vert \boldsymbol{x} \Vert\)。

（1）正定性。\(r(\boldsymbol{x})>0\)，且\(r(\boldsymbol{x})=0\)的充要条件为\(\boldsymbol{x}=0\)。

（2）齐次性。\(r(a\boldsymbol{x})=ar(\boldsymbol{x})\)，其中\(a\)为任意标量。

（3）三角不等式。对向量\(\boldsymbol{x}\)和\(\boldsymbol{y}\)，有\(r(\boldsymbol{x} + \boldsymbol{y}) \le r(\boldsymbol{x}) + r(\boldsymbol{y})\)。

范数的形式多种多样，下式中定义的范数操作就满足以上3个条件：

\[\Vert \boldsymbol{x} \Vert_p = \left( |x_1|^p + |x_2|^p + \dots + |x_n|^p \right)^{1/p} = \left( \sum_{i=1} ^n |x_i|^p \right)^{1/p}, p = 1,2,\dots \text{且} \Vert \boldsymbol{x} \Vert_{\infty} = \max_{1 \le i \le n} |x_i| \]

式中，\(\Vert \boldsymbol{x} \Vert_p\)称为\(p\)-范数，其中最有用的是1阶、2阶和\(\infty\)阶范数，即

1-范数：\(\displaystyle \Vert \boldsymbol{x} \Vert_1 = |x_1| + |x_2| + \dots + |x_n|\)

2-范数：\(\displaystyle \Vert \boldsymbol{x} \Vert_2 = \left( |x_1|^2 + |x_2|^2 + \dots + |x_n|^2 \right)^{1/2}\)

\(\infty\)-范数：\(\displaystyle \Vert \boldsymbol{x} \Vert_{\infty} = \max_{1 \le i \le n} |x_i|\)

矩阵的范数是基于向量的范数定义的，其定义式如下：

\[\Vert A \Vert = \max_{x \ne 0} \dfrac{\Vert A \boldsymbol{x} \Vert}{\Vert \boldsymbol{x} \Vert} \]

与向量的范数一样，矩阵的范数最常用的也是1阶、2阶和\(\infty\)阶范数，它们的定义式如下：

\[\Vert A \Vert_1 = \max_{1 \le j \le n} \sum_{i=1}^n |a_{ij}|, \Vert A \Vert_2 = \sqrt{S_{\max} \{ A^{\mathrm{T}} A \}} \text{和} \Vert A \Vert_{\infty} = \max_{1 \le j \le n} \sum_{j=1}^n |a_{ij}| \]

式中，\(\displaystyle \sqrt{S_{\max} \{ A^{\mathrm{T}} A \}}\) 为矩阵\(A\)的最大奇异值的平方。

n=norm(v) % 返回向量v的欧几里得范数，也称为2-范数、向量模或欧几里得长度
n=norm(v,p) % 返回广义向量p-范数
n=norm(X) % 返回矩阵X的2-范数或最大奇异值，该值近似等于max(svd(X))
n=norm(X,p) % 返回矩阵X的p-范数，其中p为1、2或Inf
n=norm(X,'fro') % 返回矩阵X的Frobenius范数

>> A=[5 -2 2];
>> m=norm(A) % 计算向量的范数

m =

    5.7446

>> m=norm(A,1) % 计算向量的1-范数，该范数为元素模的总和

m =

     9

>> B=[6 0 8; -1 5 0; -5 6 0];
>> n=norm(B) % 计算矩阵的2-范数，该范数为最大奇异值

n =

   11.0410

>> S=sparse(1:15,1:15,1);
>> n=norm(S,'fro') % 计算系数矩阵的Frobenius范数

n =

    3.8730

5.1.2 矩阵的行列式

d=det(A) % 返回矩阵A的行列式

>> A=[1 4 7; 2 5 8; 3 6 9];
>> A_det=det(A)

A_det =

     0

>> B=[1 5 12; 2 8 18; 3 9 25];
>> B_det=det(B)

B_det =

  -14.0000

5.1.3 矩阵的秩

k=rank(A) % 用默认允许误差计算矩阵的秩
k=rank(A,tol) % 给定允许误差计算矩阵的秩

对于具有n个为质量的m个线性系统方程Ax=b，有A、b可以构成增广矩阵[A b]。当且仅当rank(A)=rank(A b)时，系统有解。如果秩等于n，系统有唯一解；如果秩小于n，系统有无数解。

>> A=[1 4 7; 2 5 8; 3 6 9];
>> A_rank=rank(A)

A_rank =

     2

5.1.4 矩阵的迹

b=trace(A) % 计算矩阵A的对角元素之和

>> A=[1 4 7; 2 5 8; 3 6 9];
>> A_trace=trace(A)

A_trace =

    15

5.1.5 特征值和特征向量

一个\(n \times n\) 的方阵 \(A\) 的特征值和特征向量满足下列关系式：

\[A \nu = \lambda \nu \]

其中，\(\lambda\) 为一个标量，\(\nu\) 为一个向量。如果把矩阵 \(A\) 的所有 \(n\) 个特征值放在矩阵 \(D\) 的对角线上，则相应的特征向量按照与特征值对应的顺序排列，作为矩阵 \(V\) 的列，此时特征值问题可以改写为

\[AV=VD \]

如果矩阵\(V\) 是非奇异的，则该问题可以认为是一个特征值分解问题，此时关系式如下：

\[A=VDV^{-1} \]

e=eig(A) % 返回一个列向量，包含矩阵A的所有特征值
[V,D]=eig(A) % 返回特征值对角阵D和特征向量V，列对应右特征向量，满足A*V=V*D
[V,D,W]=eig(A) % 额外返回满矩阵W，列对应左特征向量，满足W'*A=D*W'
e=eig(A,B) % 返回一个列向量，包含方阵A和B的广义特征值
[V,D]=eig(A,B) % 返回A和B的广义特征值对角阵D与广义特征向量V，满足A*V=B*V*D
[V,D,W]=eig(A,B) % 额外返回满矩阵W，列对应左特征向量，满足W'*A=D*W'*B

>> A=[3 15 27; 1 8 32; -4 -12 -38];
>> [V D]=eig(A)

V =

  -0.3090 + 0.0000i   0.8042 + 0.0000i   0.8042 + 0.0000i
  -0.6617 + 0.0000i  -0.0718 + 0.5580i  -0.0718 - 0.5580i
   0.6831 + 0.0000i  -0.0857 - 0.1712i  -0.0857 + 0.1712i


D =

 -24.5658 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i
   0.0000 + 0.0000i  -1.2171 + 4.6607i   0.0000 + 0.0000i
   0.0000 + 0.0000i   0.0000 + 0.0000i  -1.2171 - 4.6607i

5.1.6 矩阵的逆

Y=inv(X) % 用默认允许误差计算矩阵的秩

>> X=[1 0 2; -1 5 0; 0 3 -9];
>> Y=inv(X)

Y =

    0.8824   -0.1176    0.1961
    0.1765    0.1765    0.0392
    0.0588    0.0588   -0.0980

>> I=Y*X

I =

    1.0000    0.0000   -0.0000
         0    1.0000   -0.0000
         0   -0.0000    1.0000

5.1.7 矩阵的正交空间

Q=orth(A) % 返回矩阵A的正交空间Q

>> A=[1 4 7; 2 5 8; 3 6 9];
>> Q=orth(A) % 求矩阵A的正交空间

Q =

   -0.4797    0.7767
   -0.5724    0.0757
   -0.6651   -0.6253

>> TA=rank(A) % 求矩阵A的秩

TA =

     2

>> TQ=rank(Q) % 求矩阵Q的秩

TQ =

     2

5.1.8 矩阵的化零矩阵

Z=null(A) % 返回矩阵A的一个化零矩阵（零空间的标准正交基），不存在，则返回空矩阵
Z=null(A,'r') % 返回有理数形式的化零矩阵（零空间的有理基，它通常不是正交基）

>> A=[1 4 7; 2 5 8; 3 6 9];
>> Z=null(A) % 求化零矩阵

Z =

    0.4082
   -0.8165
    0.4082

>> AZ=A*Z

AZ =

   1.0e-14 *

    0.0888
         0
   -0.1332

>> Zr=null(A,'r') % 求有理数形式的化零矩阵

Zr =

     1
    -2
     1

>> AZr=A*Zr

AZr =

     0
     0
     0

5.1.9 矩阵约化行阶梯形式

R=rref(A) % 使用高斯消元法和部分主消元法返回矩阵A的约化行阶梯形式R
R=rref(A,tool) % 以tol作为误差容限
[R,jb]=rref(A) % 返回矩阵A的约化行阶梯形式R，并返回1*r的向量jb，使r为A的秩；A(:,jb)是A的列向量构成的线性空间；R(1:r,jb)是r*r的单位矩阵

>> A=[8 1 6; 3 5 7; 4 9 2];
>> R=rref(A)

R =

     1     0     0
     0     1     0
     0     0     1

>> t=(rank(A)==rank(R))

t =

  logical

   1

5.1.10 矩阵空间夹角

Th=subspace(A,B) % 返回矩阵A和矩阵B之间的夹角

>> A=[1 4 7; 2 5 8; 3 6 9; 10 12 16];
>> B=[1 15 23; 14 11 5; 8 13 29; 2 4 6];
>> Th=subspace(A,B)

Th =

    1.5480

5.2 矩阵分解

函数	功能描述	函数	功能描述
chol	Cholesky分解	qr	正交三角分解（QR分解）
ichol	稀疏矩阵的不完全Cholesky分解	svd	奇异值分解
lu	矩阵LU分解	gsvd	广义奇异值分解
ilu	稀疏矩阵的不完全LU分解	schur	舒尔分解

5.2.1 Cholesky分解

5.2.1.1 chol函数

R=chol(A) % 将A分解为满足A=R'*R的上三角矩阵R，其中，A为对称正定矩阵，若A不是，那么将返回出错信息
[R,p]=chol(A) % 返回两个参数，并且不会返回出错信息

5.2.1.2 ichol函数

L=ichol(A) % 使用零填充对A执行不完全Cholesky分解
L=ichol(A,opts) % 使用opts指定的选项对A执行不完全Cholesky分解

>> A=[1 1 1 2; 1 4 2 1; 1 2 20 8; 2 1 8 40]; % A为正定矩阵
>> R=chol(A)

R =

    1.0000    1.0000    1.0000    2.0000
         0    1.7321    0.5774   -0.5774
         0         0    4.3205    1.4659
         0         0         0    5.7895

>> B=[1 0 6 0; 0 18 0 60; 6 0 42 0; 0 60 0 78]; % B为非正定矩阵
>> R=chol(B)
错误使用 chol
矩阵必须为正定矩阵。
 
>> Rinf=ichol(sparse(A)); % 函数sparse将矩阵A转换为稀疏矩阵
>> Rinf=full(Rinf) % 函数full将稀疏矩阵转换为满储存结构

Rinf =

    1.0000         0         0         0
    1.0000    1.7321         0         0
    1.0000    0.5774    4.3205         0
    2.0000   -0.5774    1.4659    5.7895

5.2.2 LU分解

5.2.2.1 lu函数

[L,U]=lu(A) % 将矩阵A分解为一个上三角矩阵U和一个经过置换的下三角矩阵L，满足A=L*U
[L,U,P]=lu(A) % 返回满足A=P'*L*U的置换矩阵P，L是单位下三角矩阵，U是上三角矩阵

det(A)=det(L)*det(U)
inv(A)=inv(U)*inv(L)

5.2.2.2 ilu函数

ilu(A,setup) % 计算A的不完全LU分解，返回L+U-speye(size(A))
[L,U]=ilu(A,setup) % 分别在L和U中返回单位下三角矩阵和上三角矩阵
[L,U,P]=ilu(A,setup) % 返回L中的单位下三角矩阵、U中的上三角矩阵和P中的置换矩阵

>> A=[1 4 7; 2 5 8; 3 6 9];
>> [L,U,P]=lu(A)

L =

    1.0000         0         0
    0.3333    1.0000         0
    0.6667    0.5000    1.0000


U =

     3     6     9
     0     2     4
     0     0     0


P =

     0     0     1
     1     0     0
     0     1     0

5.2.3 QR分解

X=qr(A) % 返回QR分解A=Q*R的上三角R因子，当A为满矩阵时，R=triu(X)；当A为稀疏矩阵时，R=X
[Q,R]=qr(A) % 对m*n的矩阵A执行QR分解，满足A=Q*R，适用于满矩阵和稀疏矩阵，因子R是m*n的上三角矩阵，因子Q是m*m的正交矩阵
[Q,R,E]=qr(A) % R是上三角矩阵，Q为正交矩阵，E为置换矩阵，它们满足A*E=Q*R，选择的矩阵E使得abs(diag(R))是降序排列的。适用于满矩阵
R=qr(A,0) % 精简方式返回上三角矩阵R
[Q,R]=qr(A,0) % 精简方式QR分解。适用于满矩阵和稀疏矩阵；设矩阵A是一个m*n的矩阵，若m>n，则只计算矩阵Q的前n列元素，R为n*n的矩阵；若m≤n，则其效果与[Q,R]=qr(A)的效果一致
[Q,R,E]=qr(A,0) % 精简方式QR分解，E是置换向量，满足A(:,E)=Q*R。适用于满矩阵
[C,R]=qr(A,B) % 矩阵B必须与矩阵A具有相同的行数，矩阵R是上三角矩阵，C=Q'*B；使用C和R计算稀疏线性方程组S*X=B和X=R\C的最小二乘解
[C,R,P]=qr(S,B) % 额外返回置换矩阵P；使用C、R、P计算稀疏线性方程组S*X=B和X=P*(R\C)的最小二乘解

>> A=[1 4 7; 2 5 8; 3 6 9];
>> A_rank=rank(A);
>> disp(['矩阵A的秩' num2str(A_rank)]);
矩阵A的秩2
>> [Q,R]=qr(A)

Q =

   -0.2673    0.8729    0.4082
   -0.5345    0.2182   -0.8165
   -0.8018   -0.4364    0.4082


R =

   -3.7417   -8.5524  -13.3631
         0    1.9640    3.9279
         0         0    0.0000

5.3 线性方程组

X=A\B % 表示求矩阵AX=B的解
X=A/B % 表示求矩阵XA=B的解

>> A=[8 1 6; 2 5 7; 3 9 2];
>> B=[1; 2; 3];
>> X=A\B

X =

    0.0463
    0.3059
    0.0540

观测数据：

x	0	0.25	0.5	0.75	1	1.25	1.5	1.75	2	2.25
y	-0.001	0.8	2.2	5.6	12.5	20.8	32.4	45.6	60	98.8

新建“脚本 OverdEx.m 文件”

clear
x=(0:0.25:2.25); % 用矩阵形式表示x
y=([-0.001 0.8 2.2 5.6 12.5 20.8 32.4 45.6 60 98.8])'; % 用矩阵形式表示y
A(:,1)=x'; % 构造系数矩阵A
A(:,2)=x'.^2;
b=A\y % 方程组可以写成A*[b1 b2]'=y，然后用\求系数a和b

>> OverdEx

b =

  -13.0750
   23.6278

>> x=0:0.25:3;
>> y=-13.075*x+23.6278*x.^2;
>> plot(x,y,'-',x,y,'o');
>> grid

5.4 非线性矩阵运算

函数	功能描述	函数	功能描述
expm	矩阵指数运算	sqrtm	矩阵开平方运算
logm	矩阵对数运算	funm	一般非线性矩阵运算

5.4.1 矩阵指数运算

Y=expm(X) % 返回矩阵X的指数

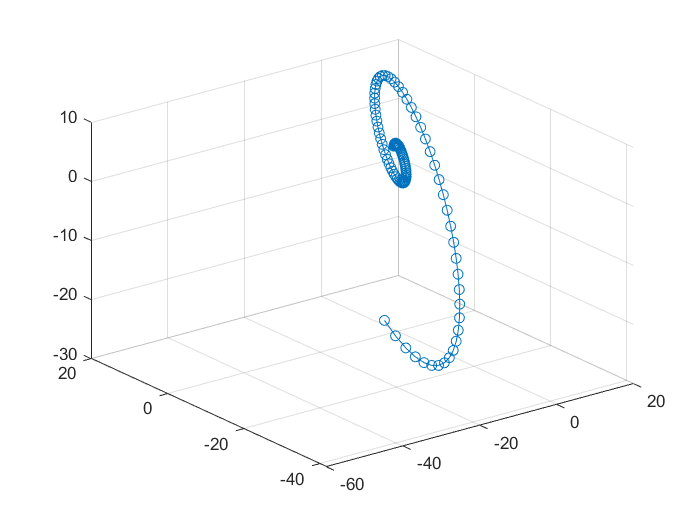
新建“脚本 expmEx.m 文件”

A=[1 0 5; 2 -4 8; -5 3 -1];
x0=[0; 1; 1];
t=0:0.03:3;
xt=[];
for i=1:length(t)
    xt(i,:)=expm(t(i)*A)*x0;
end
plot3(xt(:,1),xt(:,2),xt(:,3),'-o')
grid on;

5.4.2 矩阵对数运算

L=logm(A) % 返回矩阵A的对数L，即expm(A)的倒数
[L,exitflag]=logm(A) % 返回矩阵A的对数L，同时返回标量exitflag

>> A1=[1 4 7; 2 5 8; 3 6 9];
>> B=expm(A1)

B =

   1.0e+06 *

    1.1189    2.5339    3.9489
    1.3748    3.1134    4.8520
    1.6307    3.6929    5.7552

>> A2=logm(B)

A2 =

    1.0000    4.0000    7.0000
    2.0000    5.0000    8.0000
    3.0000    6.0000    9.0000

5.4.3 矩阵开平方运算

X=sqrtm(A) % 返回矩阵A的平方根X(X*X=A)，若矩阵A是奇异的，则返回警告信息
[X,resnorm]=sqrtm(A) % 返回残差resnorm，不返回非警告信息
[X,alpha,condx]=sqrtm(A) % 返回稳定因子alpha，矩阵X的平方根条件数估计condx

>> A=[1 -12 8; 2 25 -16; -3 36 27];
>> B=sqrtm(A)

B =

    1.3237   -2.0946    0.7115
    0.1847    5.4719   -1.4504
   -0.5134    3.1402    5.6498

>> BB=B*B

BB =

    1.0000  -12.0000    8.0000
    2.0000   25.0000  -16.0000
   -3.0000   36.0000   27.0000

5.4.4 一般非线性矩阵运算

F=fun(A,fun) % 计算在方阵参数为A时定义的函数fun，其中fun是一个函数句柄

函数名	调用格式	函数名	调用格式
exp	funm(A,@exp)	cos	funm(A,@cos)
log	funm(A,@log)	sinh	funm(A,@sinh)
sin	funm(A,@sin)	cosh	funm(A,@cosh)

>> A=[1 -2 8; 2 4 -1; -3 9 12];
>> A_cos=funm(A,@cos)

A_cos =

  -56.5160   38.3912   42.3732
    3.1211  -46.0226    2.0372
   -5.5119   64.6900   -2.5424

posted @ 2026-01-12 09:07 Zhuye_inking 阅读(49) 评论(0) 收藏举报

刷新页面返回顶部

inking

第5章 矩阵运算

第5章 矩阵运算

5.1 矩阵分析基础

5.1.1 向量的范数

5.1.2 矩阵的行列式

5.1.3 矩阵的秩

5.1.4 矩阵的迹

5.1.5 特征值和特征向量

5.1.6 矩阵的逆

5.1.7 矩阵的正交空间

5.1.8 矩阵的化零矩阵

5.1.9 矩阵约化行阶梯形式

5.1.10 矩阵空间夹角

5.2 矩阵分解

5.2.1 Cholesky分解

5.2.1.1 chol函数

5.2.1.2 ichol函数

5.2.2 LU分解

5.2.2.1 lu函数

5.2.2.2 ilu函数

5.2.3 QR分解

5.3 线性方程组

5.4 非线性矩阵运算

5.4.1 矩阵指数运算

5.4.2 矩阵对数运算

5.4.3 矩阵开平方运算

5.4.4 一般非线性矩阵运算

公告

第5章矩阵运算

第5章矩阵运算