容斥学习笔记

今天孔老爷讲容斥。感觉理解深了很多，记录一下重点。

基础容斥公式：

\[g_S=\sum_{T\subseteq S} f_S\\ f_{S}=\sum_{S\subseteq T} (-1)^{|T|-|S|}g_T \]

---

对于容斥的题目一般套路：

题目有若干条件，考虑部分满足条件，部分违背条件等作为 \(g\)。

在计算 \(g\) 的过程中，若要求指数复杂度则 \(f_{S,其他信息}\)，来做 DP，否则枚举集合的一些共通性质（常见的有集合大小等）对于满足性质的集合做 DP（通常可以不用暴力枚举集合算出来），再把所有的整合到一起。

---

二项式反演：特殊的容斥，当集合大小相同就满足 \(g\) 相同时的容斥。

---

LGV：平面 dag，条件为若干对 \(a,b\)，他们到达的方案数为 \(f_{a\to b}\)，求每个 \(a\) 到 \(b\) 的路径都不相交的方案。

若 \(a\to b\)，\(c\to d\) 相交了，那 \(a\to c\)，\(b\to d\) 也相交了且都是两种情况。于是前者减后者就是不相交方案书即 \(f_{a\to b}f_{c\to d}-f_{a\to c}f_{b\to d}\)，看出来是行列式，推广一下，变成 \(\det\) 邻接矩阵。

套路：将题目模型转化为路径的模型。常见套路：DP 转等高线。

或者更多的情况是套用 LGV 的思想与证明。

---

min-max 容斥

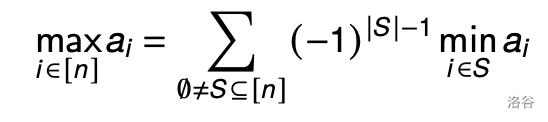
证明不用管，感性理解，把数当集合容斥。

在期望上也成立。

套路：求干完所有事的时间期望，相当于干一件事的最大值期望时间，用minmax容斥转为最小值做。