浅谈斜率优化 DP

由于作者去年 tg 都没一等，文中有错误请大家多多提出。

斜率优化是用来求解一系列 dp 方程形如 \(f_i=\displaystyle\min_{j=1}^{i}\{f_j+a_i+b_j+x_i\times y_j\}\)（其中 \(a_i\) 表示只和 \(i\) 有关的项，\(b_j\) 为只和 \(j\) 有关的项，\(x_i\times y_j\) 表示 \(i\) 有关的项和 \(j\) 有关的项相乘得到的项）。

显然转移方程中 \(\min\) 换为 \(\max\) 也同理。

考虑把转移方程化简，得到 \(f_i=\displaystyle\min_{j=1}^{i}\{f_j+b_j+x_i\times y_j\}+a_i\)，此时，我们把上式与一次函数的截距联系起来，令 \(Y=f_j+b_j,k=-x_i,X=y_j\)，此时方程即可化为 \(f_i=\displaystyle\min_{j=1}^{i}\{Y-kX\}+a_i\)。

此时，根据一次函数定义，可以得到 \(Y-kX\) 表示的是经过经过点 \((X,Y)\) 的斜率为 \(k\) 的直线的截距。所以我们只需要将斜率为 \(k\) 的直线从下往上（如果是 \(\max\) 就从上往下）贴合决策点，第一次经过的决策点即为更新 \(f_i\) 最优的点。

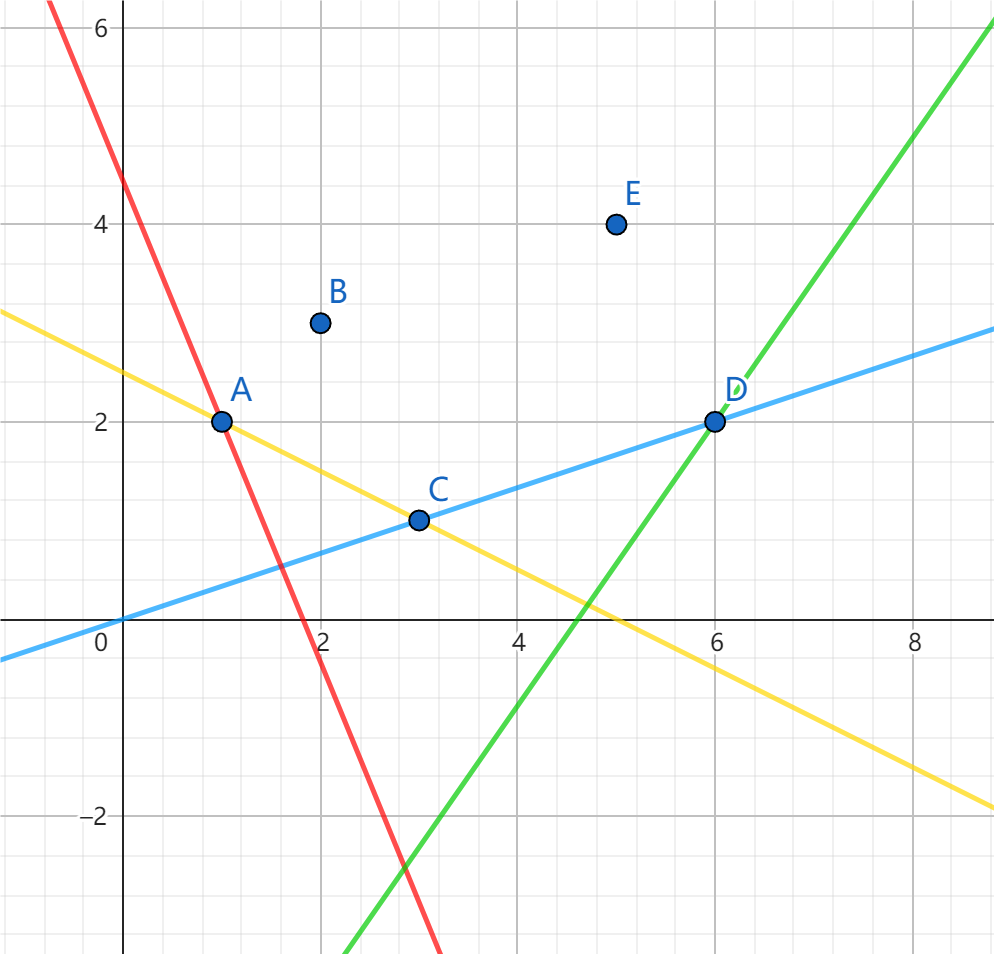
通过观察以下图，可以发现中间的点 \(B\) 和 \(E\) 一定不会被任一斜率的最优直线经过，只有在下凸壳上的点才有可能对答案有贡献（大家别被下凸壳给吓到了，这里其实只是一个名词，与实际代码没有关系）。

如果 \(k,x\) 均对于 \(i\) 单调递增，那么那么可以用单调队列实现，如果仅 \(x\) 递增，那么可以用二分实现，其他情况可以用平衡树/CDQ分治等算法优化，这里不展开（主要是作者根本不会 23333）。

模板

还是上式转移方程对应的代码，这里给出 \(k,x\) 均对于 \(i\) 递增的做法：

int f[N],q[N];
int hh = 0,tt = -1;
q[++tt] = 0;
// 这里 Y (i),X (i),K (i) 就是上式中推出的式子中的 Y,X,k
double slope (int i,int j) {
    return (Y (j) - Y (i)) / (X (j) - X (i));
}
for (int i = 1;i <= n;i++) {
    while (hh < tt && slope (q[hh],q[hh + 1]) < K (i)) hh++;
    f[i] = f[q[hh]] + a[i] + b[q[hh]] + x[i] * y[q[hh]]; //转移方程
    while (hh < tt && slope (q[tt - 1],q[tt]) > slope (q[tt],i)) tt--;
    q[++tt] = i;
}

P2120

这里不选取任务安排系列的题目原因是非斜率优化部分过于麻烦。

下文中 \(d_i\) 即为原题面中的 \(x_i\)。

考虑列出暴力转移方程 \(f_i=\displaystyle\min_{j=0}^{i-1}\{f_j+c_i+\sum_{k=j+1}^{i}p_k\times(d_i-d_k)\}\)。（这里 \(k\) 的范围为 \(i\) 其实会好写一些，后面有解释）

展开，得到 \(*=\displaystyle\min_{j=0}^{i-1}\{f_j+c_i+(\sum_{k=j+1}^{i}p_k\times d_i)- (\sum_{k=j+1}^{i}p_k\times d_k)\}\)。

继续化简得到 \(*=\displaystyle\min_{j=0}^{i-1}\{f_j+c_i+d_i\times(\sum_{k=j+1}^{i}p_k)- (\sum_{k=j+1}^{i}p_k\times d_k)\}\)。

令 \(g_{1,i}=\displaystyle\sum_{j=1}^i p_j\)，\(g_{2,i}=\displaystyle\sum_{j=1}^i (p_j\times d_j)\)。

那么得到 \(*=\displaystyle\min_{j=0}^{i-1}\{f_j+c_i+d_i\times(g_{1,i}-g_{1,j})- (g_{2,i}-g_{2,j})\}\)。

展开并添加括号得到 \(*=\displaystyle\min_{j=0}^{i-1}\{f_j+g_{2,j}-d_i\times g_{1,j}\}+c_i+d_i\times g_{1,i}-g_{2,i}\)。

令 \(Y=f_j+g_{2,j},k=d_i,X=g_{1,j}\)，那么 \(\min\) 里的项就是 \(\displaystyle\min_{j=0}^{i-1}\{Y-kX\}\)，显然可以用前面的式子进行优化。

注意到 \(k\) 关于 \(i\) 递增而递增，所以我们可以用单调队列维护下凸壳。

下面给出核心代码：

LL Y (int i) {
	return f[i] + g2[i];
}
LL X (int i) {
	return g1[i];
}
LL K (int i) {
	return x[i];
}
double slope (int i,int j) {
	if (X (i) == X (j)) return Y (j) - Y (i) > 0 ? 9e18 : -9e18;	// 特判斜率正负无穷大
	return (Y (j) - Y (i)) / (X (j) - X (i));
}

x[++n] = 3e9;	// 添加哨兵，这题数据比较恶心
for (int i = 1;i <= n;i++) g1[i] = g1[i - 1] + p[i],g2[i] = g2[i - 1] + p[i] * x[i]; 
int hh = 0,tt = -1;
q[++tt] = 0;
for (int i = 1;i <= n;i++) {
	while (hh < tt && slope (q[hh],q[hh + 1]) < K (i)) hh++;
	f[i] = f[q[hh]] + x[i] * (g1[i] - g1[q[hh]]) - (g2[i] - g2[q[hh]]) + c[i];
//	cout << q[hh] << endl;
	while (hh < tt && slope (q[tt - 1],q[tt]) > slope (q[tt],i)) tt--;
	q[++tt] = i;
}

简单总结一下，我们对于上述类似的转移方程，我们设 \(Y\) 等于仅和 \(j\) 有关的项，\(k\) 等于有关 \(i\) 的项和有关 \(j\) 的项相乘的项中的 \(i\) 的项（就是 \(x_i\times y_j\) 中的 \(x_i\)），\(X\) 等于有关 \(i\) 的项和有关 \(j\) 的项相乘的项中的 \(j\) 的项（就是 \(x_i\times y_j\) 中的 \(y_j\)）。

这样就讲完了最最最模板的斜率优化了。

求个赞不过分吧 QaQ