烟台CSP-S核心算法DAY 2

线段树日！！！（qwq）

其实树状数组就是废物——zhx

所以为什么线段树如此伟大？

特点

数据结构的90%

区间操作的KING

“种植”线段树

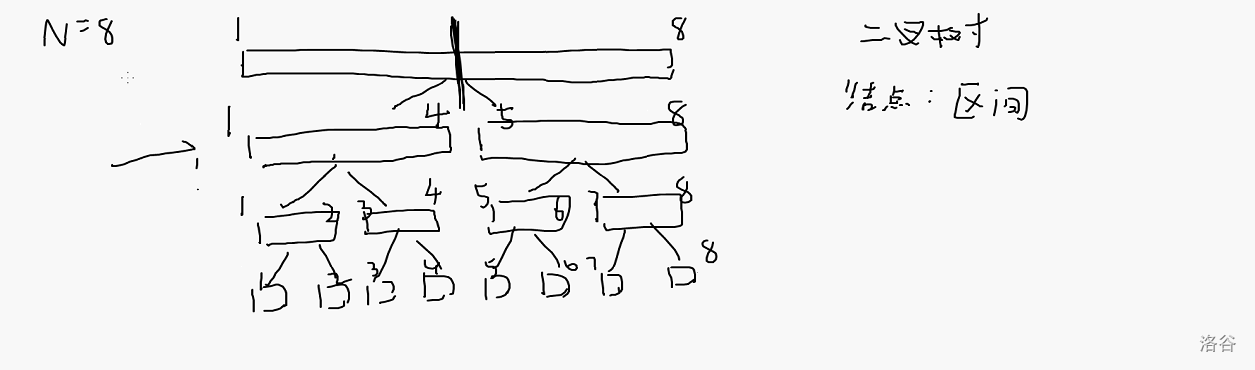
节点数：$2N$

基本思路：通过左区间和右区间的合并操作来解决父节点的操作（区间加法）

做区间操作是保证时间复杂度为$O(logN)$

数组开空间的时候，要记得开4倍$(MAXN << 2)$，因为它的标号方式不一定是到$2N$

王铭宇CODE

点击查看代码

#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>

using namespace std;
const int N = 10000005;
typedef long long ll;

int n;
ll a[N];
ll sum[N << 2];
ll mx[N << 2];
ll tag[N];

int ls(int x)
{
  return x << 1;
}
int rs(int x)
{
  return x << 1 | 1;
}
void pushup(int x)
{
  sum[x] = sum[ls(x)] + sum[rs(x)];
  mx[x] = max(mx[ls(x)], mx[rs(x)]);
}
void add(int x, int l, int r, ll k)
{
  sum[x] += k * (r - l + 1);
  mx[x] += k;
  tag[x] += k;
}
void pushdown(int x, int l, int r)
{
  int mid = (l + r) >> 1;
  if (tag[x] != 0)
  {
    add(ls(x), l, mid, tag[x]);
    add(rs(x), mid + 1, r, tag[x]);
    tag[x] = 0;
  }
}
void build(int x, int l, int r)
{
  if (l == r)
  {
    sum[x] = mx[x] =  a[l];
    return ;
  }
  int mid = (l + r) >> 1;
  build(ls(x), l, mid);
  build(rs(x), mid + 1, r);
  pushup(x);
}
ll query_sum(int x, int l, int r, int L, int R)
{
  if (L <= l && r <= R)
    return sum[x];
  pushdown(x, l, r);
  ll ret = 0;
  int mid = (l + r) >> 1;
  if (L <= mid)
  {
    ret += query_sum(ls(x), l, mid, L, R);
  }
  if (mid < R)
  {
    ret += query_sum(rs(x), mid + 1, r, L, R);
  }
  return ret;
}
ll query_max(int x, int l, int r, int L, int R)
{
  if (L <= l && r <= R)
    return mx[x];
  pushdown(x, l, r);
  ll ret = -2e9;
  int mid = (l + r) >> 1;
  if (L <= mid)
  {
    ret = max(ret, query_max(ls(x), l, mid, L, R));
  }
  if (mid < R)
  {
    ret = max(ret, query_max(rs(x), mid + 1, r, L, R));
  }
  return ret;
}
void add_one(int x, int l, int r, int p, int k)
{
  if (l == r)
  {
    sum[x] += k;
    mx[x] += k;
    return;
  }
  pushdown(x, l, r);
  int mid = (l + r) >> 1;
  if (p <= mid)
    add_one(ls(x), l, mid, p, k);
  else
    add_one(rs(x), mid + 1, r, p, k);
  pushup(x);
}
void add_many(int x, int l, int r, int L, int R, ll k)
{
  if (L <= l && R >= r)
  {
    add(x, l, r, k);
    return ;
  }
  pushdown(x, l, r);
  int mid = (l + r) >> 1;
  if (L <= mid)
    add_many(ls(x), l, mid, L, R, k);
  if (mid < R)
    add_many(rs(x), mid + 1, r, L, R, k);
  pushup(x);
}

int main()
{
  
  int m;
  cin >> n >> m;
  for (int i = 1; i <= n; ++i)
  {
    cin >> a[i];
  }
  build(1, 1, n);
  while (m--)
  {
    int opt;
    cin >> opt;
    if (opt == 1)
    {
      int x, y;
      ll k;
      cin >> x >> y >> k;
      add_many(1, 1, n, x, y, k);
    }
    if (opt == 2)
    {
      int x, y;
      cin >> x >> y;
      cout << query_sum(1, 1, n, x, y) << '\n';
    }
  }
  return 0;
}

zhx CODE（理论较优）

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1e5 + 7;

int read()
{
    int x = 0, w = 1;
	char ch = getchar();
    while(ch > '9' || ch < '0')
	{
		if(ch == '-')
		{
			w = -1;
			ch = getchar();
		}
	}
    while(ch <= '9' && ch >= '0')
	{
    	x = x * 10 + ch - '0';
		ch = getchar();
	}
    return x * w;
}

long long Qmi(int a, int b, int p)
{
	if(b == 0)
	{
		return 1%p;
	}

	if(b == 1)
	{
		return a%p;
	}

	long long ans = Qmi(a, b/2, p);

	ans = ans*ans%p;

	if(b % 2)
	{
		ans = ans*a%p;
	}

	return ans % p;
}

bool isprime(long long x)
{
	if(x <= 1)
	{
		return false;
	}
	if(x == 2)
	{
		return true;
	}
	if(x % 2 == 0)
	{
		return false;
	}
	for(int i = 3;  i <= sqrt(x);  i += 2)
	{
	   if(x % i == 0)
	   {
	   		return false;
	   }
	}
	return true;
}

#define root 1,n,1
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1

const int maxn=100010;

int n,m,a[maxn];

struct node//一个线段树节点 
{
	int sum;//代表区间和
	int size;//代表区间长度 
	int add;//这段区间被整体加了多少
	node()
	{
		sum = size = add = 0;
	} 
	void init(int v)//用一个数初始化 
	{
		sum = v;
		size = 1;
	}
}z[maxn<<2];//z[i]就代表线段树的第i个节点 

node operator+(const node &l,const node &r)
{
	node res;
	
	res.sum = l.sum + r.sum;
	res.size = l.size + r.size;
	
	return res;
}

void color(int l,int r,int rt,int v)//给l,r,rt这个节点打一个+v的懒标记
{
	z[rt].add += v;
	z[rt].sum += z[rt].size * v;
} 

void push_col(int l,int r,int rt)//标记下放 把标记告诉儿子
{
	if (z[rt].add == 0) return; //没标记 不需要下放  可以不要这句话 但会慢些 
	int m=(l+r)>>1;
	color(lson,z[rt].add);
	color(rson,z[rt].add);
	z[rt].add=0;
} 

void build(int l,int r,int rt)//建树 初始化l,r,rt这个节点 
//编号为rt的线段树节点 所对应的区间是l~r 
{
	if (l==r)
	{
		z[rt].init(a[l]);
		return;
	} 
	int m=(l+r) >> 1;
	build(lson);
	build(rson);
	z[rt] = z[rt<<1] + z[rt<<1|1]; 
}

node query(int l,int r,int rt,int nowl,int nowr)
//l,r,rt描述了一个线段树节点
//nowl nowr代表了询问的区间的左端点和右端点 
{
	if (nowl <= l && r <= nowr) return z[rt];
	push_col(l,r,rt);
	int m=(l+r)>>1;
	if (nowl<=m)
	{
		if (m<nowr) return query(lson,nowl,nowr) + query(rson,nowl,nowr);
		else return query(lson,nowl,nowr);
	}
	else return query(rson,nowl,nowr);
}

void modify(int l,int r,int rt,int nowl,int nowr,int v)
//把nowl~nowr这段区间全部整体+v 
{
	if (nowl<=l && r<=nowr)//当前线段树节点被修改区间整体包含
	{
		color(l,r,rt,v);//给l,r,rt这个节点打一个+v的懒标记
		return; 
	} 
	push_col(l,r,rt);
	int m=(l+r)>>1;
	if (nowl<=m) modify(lson,nowl,nowr,v);
	if (m<nowr) modify(rson,nowl,nowr,v);
	z[rt] = z[rt<<1] + z[rt<<1|1];
}

int main()
{
	cin >> n;
	for (int i=1;i<=n;i++)
		cin >> a[i];
	build(root);
	cin >> m;
	for (int i=1;i<=m;i++)
	{
		int opt;
		cin >> opt;
		if (opt==1)//询问
		{
			int l,r;
			cin >> l >> r;
			cout << query(root,l,r).sum << "\n";
		} 
		else
		{
			int l,r,v;
			cin >> l >> r >> v;
			modify(root,l,r,v);
		}
	}
		
	return 0;

zhx CODE（理论较优）

点击查看代码

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1e5 + 7;

int read()
{
    int x = 0, w = 1;
	char ch = getchar();
    while(ch > '9' || ch < '0')
	{
		if(ch == '-')
		{
			w = -1;
			ch = getchar();
		}
	}
    while(ch <= '9' && ch >= '0')
	{
    	x = x * 10 + ch - '0';
		ch = getchar();
	}
    return x * w;
}

long long Qmi(int a, int b, int p)
{
	if(b == 0)
	{
		return 1%p;
	}

	if(b == 1)
	{
		return a%p;
	}

	long long ans = Qmi(a, b/2, p);

	ans = ans*ans%p;

	if(b % 2)
	{
		ans = ans*a%p;
	}

	return ans % p;
}

bool isprime(long long x)
{
	if(x <= 1)
	{
		return false;
	}
	if(x == 2)
	{
		return true;
	}
	if(x % 2 == 0)
	{
		return false;
	}
	for(int i = 3;  i <= sqrt(x);  i += 2)
	{
	   if(x % i == 0)
	   {
	   		return false;
	   }
	}
	return true;
}

#define root 1,n,1
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1

const int maxn=100010;

int n,m,a[maxn];

struct node//一个线段树节点 
{
	int sum;//代表区间和
	int size;//代表区间长度 
	int add;//这段区间被整体加了多少
	node()
	{
		sum = size = add = 0;
	} 
	void init(int v)//用一个数初始化 
	{
		sum = v;
		size = 1;
	}
}z[maxn<<2];//z[i]就代表线段树的第i个节点 

node operator+(const node &l,const node &r)
{
	node res;
	
	res.sum = l.sum + r.sum;
	res.size = l.size + r.size;
	
	return res;
}

void color(int l,int r,int rt,int v)//给l,r,rt这个节点打一个+v的懒标记
{
	z[rt].add += v;
	z[rt].sum += z[rt].size * v;
} 

void push_col(int l,int r,int rt)//标记下放 把标记告诉儿子
{
	if (z[rt].add == 0) return; //没标记 不需要下放  可以不要这句话 但会慢些 
	int m=(l+r)>>1;
	color(lson,z[rt].add);
	color(rson,z[rt].add);
	z[rt].add=0;
} 

void build(int l,int r,int rt)//建树 初始化l,r,rt这个节点 
//编号为rt的线段树节点 所对应的区间是l~r 
{
	if (l==r)
	{
		z[rt].init(a[l]);
		return;
	} 
	int m=(l+r) >> 1;
	build(lson);
	build(rson);
	z[rt] = z[rt<<1] + z[rt<<1|1]; 
}

node query(int l,int r,int rt,int nowl,int nowr)
//l,r,rt描述了一个线段树节点
//nowl nowr代表了询问的区间的左端点和右端点 
{
	if (nowl <= l && r <= nowr) return z[rt];
	push_col(l,r,rt);
	int m=(l+r)>>1;
	if (nowl<=m)
	{
		if (m<nowr) return query(lson,nowl,nowr) + query(rson,nowl,nowr);
		else return query(lson,nowl,nowr);
	}
	else return query(rson,nowl,nowr);
}

void modify(int l,int r,int rt,int nowl,int nowr,int v)
//把nowl~nowr这段区间全部整体+v 
{
	if (nowl<=l && r<=nowr)//当前线段树节点被修改区间整体包含
	{
		color(l,r,rt,v);//给l,r,rt这个节点打一个+v的懒标记
		return; 
	} 
	push_col(l,r,rt);
	int m=(l+r)>>1;
	if (nowl<=m) modify(lson,nowl,nowr,v);
	if (m<nowr) modify(rson,nowl,nowr,v);
	z[rt] = z[rt<<1] + z[rt<<1|1];
}

int main()
{
	cin >> n;
	for (int i=1;i<=n;i++)
		cin >> a[i];
	build(root);
	cin >> m;
	for (int i=1;i<=m;i++)
	{
		int opt;
		cin >> opt;
		if (opt==1)//询问
		{
			int l,r;
			cin >> l >> r;
			cout << query(root,l,r).sum << "\n";
		} 
		else
		{
			int l,r,v;
			cin >> l >> r >> v;
			modify(root,l,r,v);
		}
	}
		
	return 0;
}

我们认为，zhx写法更加令人愉悦，毕竟有很大的灵活性和可读性，可以更容易根据题意更改线段树函数

我们对于线段树的修改与查询操作的修改，我们一般只需更改结构体内维护的变量，构造函数，左右儿子之间的合并，以及懒标记的下方，而另外的建树、修改、询问则大部分题不需要更改

如果一道线段树题有多种修改方式（对于修改与询问的更改），一定要规划好不同修改之间的顺序

对于更改线段树函数的理解，见DAY 2代码中xianduanshu1~7的问题及代码，这很重要

伟大の取模——zhx

这些取模的一般规律在DP卡常中十分重要——zhx

加法的取模规律

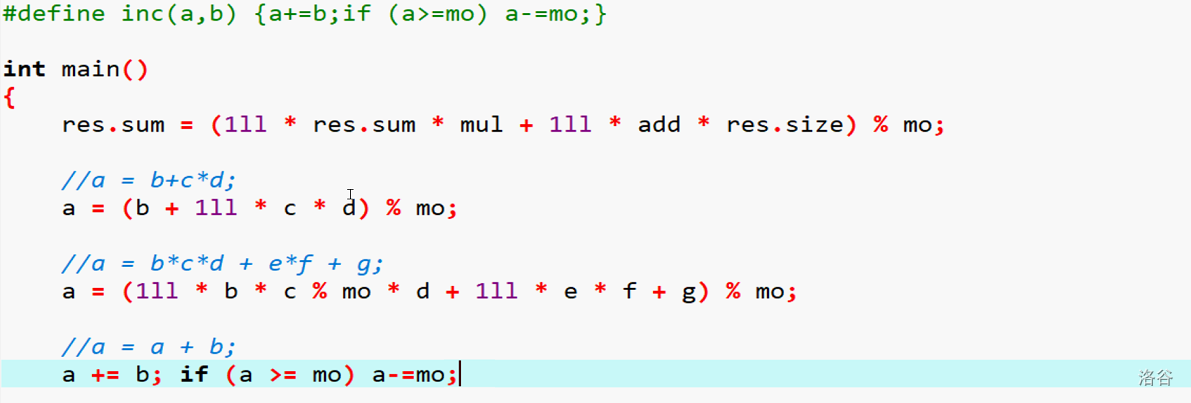
我们可以将$a += b$的取模方式写成函数ordefine

减法的取模规律

同理，我们可以将$a -= b$的取模方式写成函数ordefine

这些可以伟大的优化我们的常数（运算速度）

例CODE

点击查看代码

#include<bits/stdc++.h>

using namespace std;

const int mo = 1000000007;

inline void inc(int &a,int b)
{
	a+=b;if (a>=mo) a-=mo;
}
#define inc(a,b) {a+=b;if (a>=mo) a-=mo;}

int main()
{
	res.sum = (1ll * res.sum * mul + 1ll * add * res.size) % mo;
	
	//a = b+c*d;
	a = (b + 1ll * c * d) % mo;
	
	//a = b*c*d + e*f + g;
	a = (1ll * b * c % mo * d + 1ll * e * f + g) % mo;
	
	//a = a + b;
	a += b; if (a >= mo) a-=mo;
	
	//a = b*c-d*e
	a = ((1ll * b * c - 1ll * d * e) % mo + mo) % mo;
	
	//a = a - b
	a -= b; if (a<0) a += mo;
	
	return 0;
}

线段树再变异

GSS系列

GSS1

GSS3

GSS4

GSS5

QTREE系列

COT系列

上述为上午所有可做题，除QTREE & COT系列，重点xianduanshu1~7代码

例题

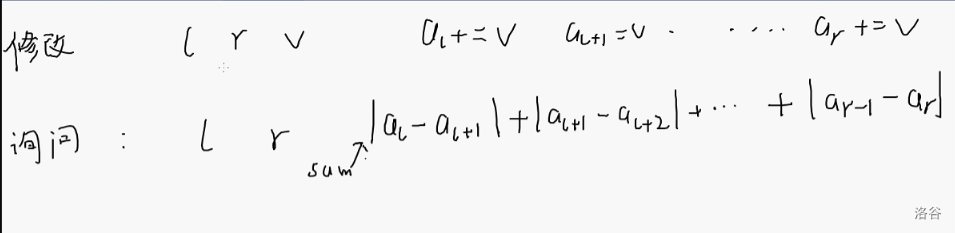
我们只需要处理左儿子的值、右儿子的值，再将两个区间中间的值进行操作即可

点击查看代码

#include <bits/stdc++.h>

using namespace std;

#define root 1, n, 1
#define lson l, m, rt << 1
#define rson m + 1, r, rt << 1 | 1

const int maxn = 100010;

int n, m, a[maxn];

struct node // 一个线段树节点
{
	int sum; // 代表区间相邻两数差的绝对值的和
	int lv;	 // 最左边的数是多少
	int rv;	 // 最右边的数是多少
	int add; // 这段区间被整体加了多少
	int size; // 区间长度
	node()
	{
		sum = add = 0;
	}
	void init(int v) // 用一个数初始化
	{
		sum = 0;
		lv = rv = v;
		size = 1;
	}
} z[maxn << 2]; // z[i]就代表线段树的第i个节点

node operator+(const node &l, const node &r)
{
	node res;

	res.sum = l.sum + r.sum + abs(l.rv - r.lv);
	res.lv = l.lv;
	res.rv = r.rv;

	return res;
}

void color(int l, int r, int rt, int v) // 给l,r,rt这个节点打一个+v的懒标记
{
	z[rt].add += v;
	z[rt].lv += v;
	z[rt].rv += v;
}

void push_col(int l, int r, int rt) // 标记下放 把标记告诉儿子
{
	if (z[rt].add == 0)
		return; // 没标记 不需要下放  可以不要这句话 但会慢些
	int m = (l + r) >> 1;
	color(lson, z[rt].add);
	color(rson, z[rt].add);
	z[rt].add = 0;
}

void build(int l, int r, int rt) // 建树 初始化l,r,rt这个节点
// 编号为rt的线段树节点 所对应的区间是l~r
{
	if (l == r)
	{
		z[rt].init(a[l]);
		return;
	}
	int m = (l + r) >> 1;
	build(lson);
	build(rson);
	z[rt] = z[rt << 1] + z[rt << 1 | 1];
}

node query(int l, int r, int rt, int nowl, int nowr)
// l,r,rt描述了一个线段树节点
// nowl nowr代表了询问的区间的左端点和右端点
{
	if (nowl <= l && r <= nowr)
		return z[rt];
	push_col(l, r, rt);
	int m = (l + r) >> 1;
	if (nowl <= m)
	{
		if (m < nowr)
			return query(lson, nowl, nowr) + query(rson, nowl, nowr);
		else
			return query(lson, nowl, nowr);
	}
	else
		return query(rson, nowl, nowr);
}

void modify(int l, int r, int rt, int nowl, int nowr, int v)
// 把nowl~nowr这段区间全部整体+v
{
	if (nowl <= l && r <= nowr) // 当前线段树节点被修改区间整体包含
	{
		color(l, r, rt, v); // 给l,r,rt这个节点打一个+v的懒标记
		return;
	}
	push_col(l, r, rt);
	int m = (l + r) >> 1;
	if (nowl <= m)
		modify(lson, nowl, nowr, v);
	if (m < nowr)
		modify(rson, nowl, nowr, v);
	z[rt] = z[rt << 1] + z[rt << 1 | 1];
}

int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++)
		cin >> a[i];
	build(root);
	cin >> m;
	for (int i = 1; i <= m; i++)
	{
		int opt;
		cin >> opt;
		if (opt == 1) // 询问
		{
			int l, r;
			cin >> l >> r;
			cout << query(root, l, r).sum << "\n";
		}
		else
		{
			int l, r, v;
			cin >> l >> r >> v;
			modify(root, l, r, v);
		}
	}

	return 0;
}

再来一道例题

P3373 线段树2 luogu

这题十分成功地告诉我们

如果一道线段树题有多种修改方式（对于修改与询问的更改），一定要规划好不同修改之间的顺序

一定要先处理好区间推平的情况，将懒标记删掉，再处理乘法，再处理加法

点击查看代码

#include <bits/stdc++.h>

using namespace std;

#define root 1, n, 1
#define lson l, m, rt << 1
#define rson m + 1, r, rt << 1 | 1

const int maxn = 100010;

int n, m, a[maxn];

struct node // 一个线段树节点
{
	int sum;	// 代表区间和
	int size; // 代表区间长度
	int add;
	int mul;
	// x*mul+add
	node()
	{
		sum = size = add = 0;
		mul = 1;
	}
	void init(int v) // 用一个数初始化
	{
		sum = v;
		size = 1;
	}
} z[maxn << 2]; // z[i]就代表线段树的第i个节点

node operator+(const node &l, const node &r)
{
	node res;

	res.sum = l.sum + r.sum;
	res.size = l.size + r.size;

	return res;
}

void color(int l, int r, int rt, int mul, int add) // 给l,r,rt这个节点打一个*mul+add的懒标记
{
	z[rt].mul *= mul;
	z[rt].add = z[rt].add * mul + add;
	z[rt].sum = z[rt].sum * mul + add * z[rt].size;
}

void push_col(int l, int r, int rt) // 标记下放 把标记告诉儿子
{
	if (z[rt].mul == 1 && z[rt].add == 0)
		return; // 没标记 不需要下放  可以不要这句话 但会慢些
	int m = (l + r) >> 1;
	color(lson, z[rt].mul, z[rt].add);
	color(rson, z[rt].mul, z[rt].add);
	z[rt].mul = 1;
	z[rt].add = 0;
}

void build(int l, int r, int rt) // 建树 初始化l,r,rt这个节点
// 编号为rt的线段树节点 所对应的区间是l~r
{
	if (l == r)
	{
		z[rt].init(a[l]);
		return;
	}
	int m = (l + r) >> 1;
	build(lson);
	build(rson);
	z[rt] = z[rt << 1] + z[rt << 1 | 1];
}

node query(int l, int r, int rt, int nowl, int nowr)
// l,r,rt描述了一个线段树节点
// nowl nowr代表了询问的区间的左端点和右端点
{
	if (nowl <= l && r <= nowr)
		return z[rt];
	push_col(l, r, rt);
	int m = (l + r) >> 1;
	if (nowl <= m)
	{
		if (m < nowr)
			return query(lson, nowl, nowr) + query(rson, nowl, nowr);
		else
			return query(lson, nowl, nowr);
	}
	else
		return query(rson, nowl, nowr);
}

void modify(int l, int r, int rt, int nowl, int nowr, int mul, int add)
// 把nowl~nowr这段区间全部整体+v
{
	if (nowl <= l && r <= nowr) // 当前线段树节点被修改区间整体包含
	{
		color(l, r, rt, mul, add); // 给l,r,rt这个节点打一个+v的懒标记
		return;
	}
	push_col(l, r, rt);
	int m = (l + r) >> 1;
	if (nowl <= m)
		modify(lson, nowl, nowr, mul, add);
	if (m < nowr)
		modify(rson, nowl, nowr, mul, add);
	z[rt] = z[rt << 1] + z[rt << 1 | 1];
}

int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++)
		cin >> a[i];
	build(root);
	cin >> m;
	for (int i = 1; i <= m; i++)
	{
		int opt;
		cin >> opt;
		if (opt == 1) // 询问
		{
			int l, r;
			cin >> l >> r;
			cout << query(root, l, r).sum << "\n";
		}
		else
		{
			int l, r, add, mul;
			cin >> l >> r >> add >> mul;
			modify(root, l, r, add, mul);
		}
	}

	return 0;
}

加题！加题！

给区间加上一个等差数列

首先，我们可以想到，给一个区间加上多个等差数列，那么他还是被加上了一个等差数列

所以，我们只需要维护好首项和公差即可

点击查看代码

#include <bits/stdc++.h>

using namespace std;

#define root 1, n, 1
#define lson l, m, rt << 1
#define rson m + 1, r, rt << 1 | 1

const int maxn = 100010;

int n, m, a[maxn];

struct node // 一个线段树节点
{
	int sum;	// 代表区间和
	int size; // 代表区间长度
	int x, y; // 给这段区间加上了一个首项为x 公差为y的等差数列
	node()
	{
		sum = size = x = y = 0;
	}
	void init(int v) // 用一个数初始化
	{
		sum = v;
		size = 1;
	}
} z[maxn << 2]; // z[i]就代表线段树的第i个节点

node operator+(const node &l, const node &r)
{
	node res;

	res.sum = l.sum + r.sum;
	res.size = l.size + r.size;

	return res;
}

void color(int l, int r, int rt, int x, int y) // 给l,r,rt这个节点加上一个首项为x公差为y的等差数列
{
	z[rt].x += x;
	z[rt].y += y;
	z[rt].sum += (x + x + (z[rt].size - 1) * y) * z[rt].size / 2;
}

void push_col(int l, int r, int rt) // 标记下放 把标记告诉儿子
{
	if (z[rt].x == 0 && z[rt].y == 0)
		return; // 没标记 不需要下放  可以不要这句话 但会慢些
	int m = (l + r) >> 1;
	color(lson, z[rt].x, z[rt].y);
	color(rson, z[rt].x + z[rt << 1].size * z[rt].y, z[rt].y);
	z[rt].x = z[rt].y = 0;
}

void build(int l, int r, int rt) // 建树 初始化l,r,rt这个节点
// 编号为rt的线段树节点 所对应的区间是l~r
{
	if (l == r)
	{
		z[rt].init(a[l]);
		return;
	}
	int m = (l + r) >> 1;
	build(lson);
	build(rson);
	z[rt] = z[rt << 1] + z[rt << 1 | 1];
}

node query(int l, int r, int rt, int nowl, int nowr)
// l,r,rt描述了一个线段树节点
// nowl nowr代表了询问的区间的左端点和右端点
{
	if (nowl <= l && r <= nowr)
		return z[rt];
	push_col(l, r, rt);
	int m = (l + r) >> 1;
	if (nowl <= m)
	{
		if (m < nowr)
			return query(lson, nowl, nowr) + query(rson, nowl, nowr);
		else
			return query(lson, nowl, nowr);
	}
	else
		return query(rson, nowl, nowr);
}

void modify(int l, int r, int rt, int nowl, int nowr, int x, int y)
// 把nowl~nowr这段区间全部整体+v
{
	if (nowl <= l && r <= nowr) // 当前线段树节点被修改区间整体包含
	{
		color(l, r, rt, x, y); // 给l,r,rt这个节点打一个+v的懒标记
		return;
	}
	push_col(l, r, rt);
	int m = (l + r) >> 1;
	if (nowl <= m)
		modify(lson, nowl, nowr, x, y);
	if (m < nowr)
		modify(rson, nowl, nowr, x, y);
	z[rt] = z[rt << 1] + z[rt << 1 | 1];
}

int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++)
		cin >> a[i];
	build(root);
	cin >> m;
	for (int i = 1; i <= m; i++)
	{
		int opt;
		cin >> opt;
		if (opt == 1) // 询问
		{
			int l, r;
			cin >> l >> r;
			cout << query(root, l, r).sum << "\n";
		}
		else
		{
			int l, r, x, y;
			cin >> l >> r >> x >> y;
			modify(root, l, r, x, y);
		}
	}

	return 0;
}

又是伟大的中午

好耶农大里面有球场

下午力

可持久化数据结构

因为一个数据结构时刻都发生变化

可持久化就是可以访问历史版本的数据结构且强制在线

我们存在许多数据结构有可持久化的模式

可持久化线段树

我们在i+1情况下会对比i的情况下做出改变

于是，我们将改变的节点新建出新的节点

注意，因为我们一定要建成可访问历史版本的线段树

所以我们做出的操作一定是新建出改变过的节点，而不是覆盖掉

我们将未作出改变的节点连到新建的节点上，就构成了一棵可持久化线段树

打个比喻：1s动画由20帧左右的静态画面连续播放而成，每两幅相邻画面之间的差别很少，如果用计算机制作动画，若每一帧的画面都重新制作，会很浪费空间，为了降低成本，让每一帧画面只记录与前一帧的不同处；（又如红绿灯的秒数倒计时）

模板CODE

点击查看代码

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1e5 + 7;

int read()
{
	int x = 0, w = 1;
	char ch = getchar();
	while(ch > '9' || ch < '0')
	{
		if(ch == '-')
		{
			w = -1;
			ch = getchar();
		}
	}
	while(ch <= '9' && ch >= '0')
	{
		x = x * 10 + ch - '0';
		ch = getchar();
	}
	return x * w;
}

long long Qmi(int a, int b, int p)
{
	if(b == 0)
	{
		return 1%p;
	}
	
	if(b == 1)
	{
		return a%p;
	}
	
	long long ans = Qmi(a, b/2, p);
	
	ans = ans*ans%p;
	
	if(b % 2)
	{
		ans = ans*a%p;
	}
	
	return ans % p;
}

bool isprime(long long x)
{
	if(x <= 1)
	{
		return false;
	}
	if(x == 2)
	{
		return true;
	}
	if(x % 2 == 0)
	{
		return false;
	}
	for(int i = 3;  i <= sqrt(x);  i += 2)
	{
		if(x % i == 0)
		{
			return false;
		}
	}
	return true;
}

int cnt;

int a[MAXN], root[MAXN];

struct node
{
	int l, r;
	
	int sum;
	
	node()
	{
		l = r = sum = 0;
	}
	
}z[MAXN*20];//应是MAXN*logn，这里logn取20

void update(int p)
{
	z[p].sum = z[z[p].l].sum + z[z[p].r].sum;
}

int build(int l, int r)
{
	cnt++;
	int p = cnt;
	
	if(l == r)
	{
		z[p].sum = a[l];
		return p;
	}
	int m = (l + r) >> 1;
	
	z[p].l = build(l, m);
	z[p].r = build(m + 1, r);
	
	update(p);
	
	return p;
}

int query(int l, int r, int rt, int nowl, int nowr)
{
	if(nowl <= l && r <= nowr)
	{
		return z[rt].sum;
	}
	
	int m = (l + r) >> 1;
	
	if(nowl <= m)
	{
		if(m < nowr)
		{
			return query(l, m, z[rt].l, nowl, nowr) + query(m+1, r, z[rt].r, nowl, nowr);	
		}
		else
		{
			return query(l, m, z[rt].l, nowl, nowr);
		}
	}
	else
	{
		return query(m+1, r, z[rt].r, nowl, nowr);
	}
}

int modify(int l, int r, int rt, int p, int v)
{
	cnt++;
	
	int q = cnt;
	
	z[q] = z[rt];
	
	if(l == r)
	{
		z[q].sum += v;
		return q;
	}
	
	int m = (l + r) >> 1;
	if(p <= m)
	{
		z[q].l = modify(l, m, z[q].l, p, v);
	}
	else
	{
		z[q].r = modify(m+1, r, z[q].r, p, v);
	}
	
	update(q);
	return q;
}

int n, m;

int main()
{
	cin>>n;
	
	for(int i = 1;  i <= n;  i++)
	{
		cin>>a[i];
	}
	
	cin>>m;
	
	root[0] = build(1, n);
	
	for(int i = 1;  i <= m;  i++)
	{
		int op;
		cin>>op;
		
		if(op == 1)
		{
			int p, v;
			cin>>p>>v;
			
			root[i] = modify(1, n, root[i-1], p, v);
		}
		else
		{
			int k, l, r;
			cin>>k>>l>>r;
			cout<<query(1, n, root[k], l, r)<<'\n';
			root[i] = root[i-1];
		}
	}
	
	return 0;
}

可持久化数组

方法1：

每个位置开一个 $vector$，存每一个修改的时间戳、值

查询的时候二分查找

方法2：

开一个 $map<pair<int, int>, int>$

这三个 $int$ 分别表示位置、时间、值

查询直接 $lower$_$bound$

前缀值域可持久化线段树（主席树）

like this

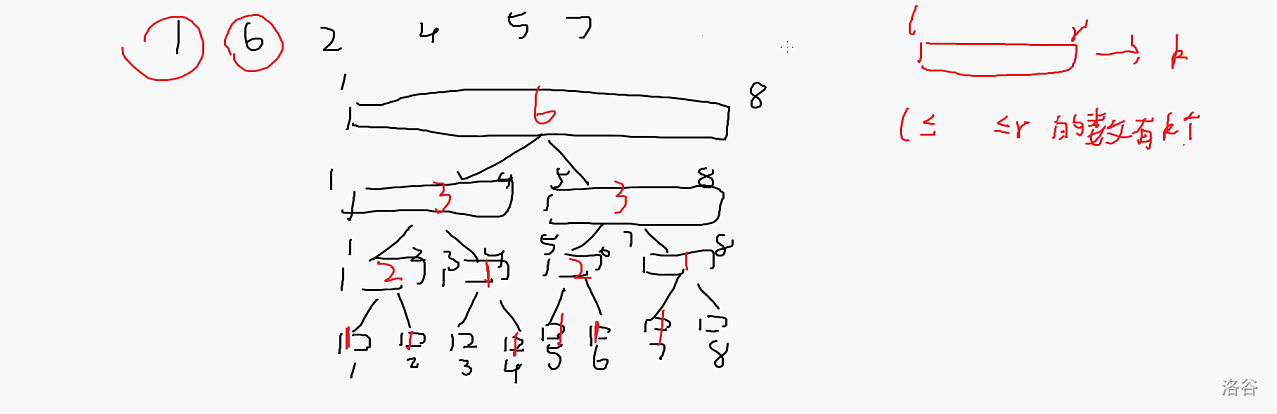
点击查看代码

#include <iostream>

using std::cin;
using std::cout;

const int N = 2e5 + 10;

struct Node
{
	int l, r; // 左儿子，右儿子
	int sum;	// 区间和
	Node()
	{
		l = r = sum = 0;
	}
} z[N * 30];

int n;
int cnt; // 节点数
int a[N];
int root[N]; // 第 i 个前缀应的值域线段树的根

void update(int p)
{
	z[p].sum = z[z[p].l].sum + z[z[p].r].sum;
}
int build(int l, int r) // 返回这段区间对应的节点编号
{
	cnt++;
	int p = cnt;
	if (l == r)
	{
		z[p].sum = a[l];
		return p;
	}
	int m = (l + r) >> 1;
	z[p].l = build(l, m);
	z[p].r = build(m + 1, r);
	update(p);
	return p;
}
int query(int p1, int p2, int l, int r, int k)
// 当前对应的值域范围 l ~ r
// 要询问第 k 小的数
// 需要 p1, p2 两棵线段树来询问
{
	if (l == r)
		return l;
	int m = (l + r) >> 1;
	if (z[z[p2].l].sum - z[z[p1].l].sum >= k)
		return query(z[p1].l, z[p2].l, l, m, k);
	else
		return query(z[p1].r, z[p2].r, m + 1, r, k - (z[z[p2].l].sum - z[z[p1].l].sum));
}
int modify(int l, int r, int rt, int p, int v)
{
	cnt++;
	int q = cnt; // 新的节点 q 用于修改
	z[q] = z[rt];
	if (l == r)
	{
		z[q].sum += v;
		return q;
	}
	int m = (l + r) >> 1;
	if (p <= m)
		z[q].l = modify(l, m, z[q].l, p, v);
	else
		z[q].r = modify(m + 1, r, z[q].r, p, v);
	update(q);
	return q;
}

int main()
{
	cin >> n;
	int MAXV = 0;
	for (int i = 1; i <= n; ++i)
		cin >> a[i], MAXV = std::max(MAXV, a[i]);
	int m;
	cin >> m;
	root[0] = 0;
	for (int i = 1; i <= n; ++i)
		root[i] = modify(1, MAXV, root[i - 1], a[i], 1);
	// 主席树就建好了
	for (int i = 1; i <= m; ++i)
	{
		int l, r, k;
		cin >> l >> r >> k;
		cout << query(root[l - 1], root[r], 1, MAXV, k);
	}
	return 0;
}

吃掉例题

可可爱爱的思考题捏

我最爱做题了

我们可以很容易的想到两种暴力的做法

一种为修改$O(1)$，查询$O(n)$的

一种为修改$O(n)$，查询$O(1)$的

我们应该思考把这两种想法综合一下，找出一种复杂度更加合理的做法，因为这种暴力的最坏复杂度是$O(n^2)$的

于是

根号分治

以 $\sqrt n$
为界限，如果一个点周围连了超过
$\sqrt n$个点，就称它为大点，否则称它为小点。

如果修改的一个点是小点，那么就直接暴力。

否则，如果这个点连的是大点，显然大点的数量不会超过
$\sqrt n$个；如果连的是小点的话，就处理出每个大点连的白小点和黑小点的数量

博客中的最后一题

bzoj 树上三角形

思考了114min，竟然是Fibonacci斐波那契数列

先用 LCA 求出 l，r 之间的路径

fib 数列任意三项都不能组成三角形

树上三角形：每个值都 $\leq$ 1e9

做 LCA

如果树上的点 $\geq $ 40，直接输出 $Yes$
$(∵fib_40 ≈ 1e9)$

否则直接暴力

题单

（完成情况见luogu题单）

十年OI一场空，不开long long见祖宗

线段树日在此终结

posted @ 2025-05-02 19:27 include_qwq 阅读(54) 评论(0) 收藏举报

刷新页面返回顶部

include_qwq

烟台CSP-S核心算法DAY 2

烟台CSP-S核心算法DAY 2

线段树日！！！（qwq）

特点

“种植”线段树

王铭宇CODE

zhx CODE（理论较优）

zhx CODE（理论较优）

伟大の取模——zhx

例CODE

线段树再变异

GSS系列

GSS1

GSS3

GSS4

GSS5

QTREE系列

COT系列

例题

再来一道例题

加题！加题！

又是伟大的中午

下午力

可持久化数据结构

可持久化线段树

模板CODE

可持久化数组

前缀值域可持久化线段树（主席树）

吃掉例题

我最爱做题了

博客中的最后一题

题单

十年OI一场空，不开long long见祖宗

线段树日在此终结

公告