烟台CSP-S核心算法DAY 1
烟台CSP-S核心算法DAY 1
上午
十分简单的数据结构
内容十分基础
但确实是不可或缺的数据结构
我们确实需要很好的掌握他们
队列 & 栈
伟大的STL
队列
#include<queue>
//#include<bits/stdc++.h>
using namespace std;
queue<int> q;
//queue<队列里面的元素类型> 变量名;
int main()
{
q.push(233);
q.push(2233);//向队列里面加入一个元素
q.pop();//从队列中删除一个元素 删除是队列头的元素 233 void类型没有返回值
int x = q.front();//获取队列头元素 2233
cout << q.size() << endl;//获取队列剩余的元素个数 1
}
栈
#include<stack>
//#include<bits/stdc++.h>
using namespace std;
stack<int> q;
//stack<队列里面的元素类型> 变量名;
int main()
{
q.push(233);
q.push(2233);//向栈里面加入一个元素
q.pop();//从栈中删除一个元素 删除是队列头的元素 2233 void类型没有返回值
int x = q.top();//获取栈顶部元素 233
cout << q.size() << endl;//获取栈剩余的元素个数 1
}
当然,特殊题目下我们存在伟大的手写
手写队列
//#include<bits/stdc++.h>
using namespace std;
struct queue
{
int a[1000];
int head=1;//队列头在哪里
int tail=0;//队列尾巴在哪里
void push(int x)
{
tail ++;
a[tail] = x;
}
void pop()
{
head++;
}
int size()
{
return tail-head+1;
}
int front()
{
return a[head];
}
}q;
int main()
{
q.push(233);
q.push(2233);//向队列里面加入一个元素
q.pop();//从队列中删除一个元素 删除是队列头的元素 233 void类型没有返回值
int x = q.front();//获取队列头元素 2233
cout << q.size() << endl;//获取队列剩余的元素个数 1
}
双端队列
#include<deque>
using namespace std;
deque<int> q;//双端队列
//q.push_front() 从前面加入
//q.pop_front() 从前面删除
//q.front() 询问前面的数是多少
//q.push_back() 从后面加入
//q.pop_back() 从后面删除
//q.back() 询问后面的数是多少
int a[maxn];
void push(int i)//单调队列的插入 插入下标为i的元素 要保证队列单调递增
{
while (q.size() > 0 && a[q.back()] >= a[i])
q.pop_back();
q.push_back(i);
}
int main()
{
cin >> n;
for (int i=1;i<=n;i++)
cin >> a[i];
cin >> m;//所有长度为m的区间的最小值
for (int i=1;i<=n;i++)
{
push(i);//向单调队列里面加入a[i]这个元素
if (i-m == q.front()) q.pop_front();//把a[i-m]这个数删掉
if (i>=m)//区间长度已经超过m了 需要取出最小值
cout << a[q.front()] << "\n";
}
}
ps:确实不常用的双端队列
双指针维护队列
int main()
{
cin >> n;
for (int i=1;i<=n;i++)
cin >> a[i];
cin >> m;
int sum=0;
for (int l=1,r=1;l<=n;sum-=a[l],l++)
{
while (sum<=m && r<=n)
{
sum += a[r];
r++;
}
if (sum>m)
{
r--;
sum -= a[r];
}
ans = max(ans,r-l);//a[l] ~ a[r-1]
}
}
ps:上述代码对应Day 1课间pdf中的题目
堆
3件事
1.大根堆,小根堆分别处理最大值和最小值
就是一个二叉树的想法
小根堆常见的建法并非vector greater...(不是我也确实不会这种建法啊qwq)
其实将大根堆的操作加上\((-)\)就可以实现
#include<queue>
//#include<bits/stdc++.h>
using namespace std;
priority_queue<int> q;
//大根堆
//小根堆最简单的方法:取负号
struct rec
{
int a,b;
};
//如果要把结构体 放入 stl比大小 只能重载小于号
bool operator<(const rec &x,const rec &y)
{
return x.a + x.b > y.a + y.b;
}
priority_queue<rec> qq;//取出a+b最小的结构体
int main()
{
q.push(233);
q.push(2233);//向堆里面加入一个元素
q.pop();//从堆中删除一个元素 删除是堆中最大的元素 2233 void类型没有返回值
int x = q.top();//获取堆中最大元素 233
cout << q.size() << endl;//获取堆剩余的元素个数 1
}
手写堆
struct heap
{
int a[1010];//堆的每一个元素
int n=0;//堆有几个元素
int top()//询问最大值
{
return a[1];
}
void push(int x)//插入一个数
{//O(logn)
n++;a[n] = x;
int p=n;
while (p!=1)
{
if (a[p] > a[p>>1])
{
swap(a[p],a[p>>1]);
p = p>>1;
}
else
{
break;
}
}
}
void pop()//删除最大值
{
swap(a[1],a[n]);n--;
int p=1;
while ((p<<1) <= n)
{
int l=p<<1;
int r=l|1;//p*2+1
int pp=l;
if (r<=n && a[r] > a[l]) pp=r;//pp一定是两个儿子中较大的那个
if (a[pp] > a[p])
{
swap(a[pp],a[p]);
p=pp;
}
else
{
break;
}
}
}
int size()//询问还有几个数
{
return n;
}
};
关于堆的其他题目见pdf以及对应的代码(文件夹中)
当然这里,堆的题目是很重要的(见pdf)
例1 AC CODE
#include <queue>
#include <iostream>
#include <algorithm>
#define a first
#define b second
#define pii std::pair<int, int>
using std::cin;
using std::cout;
using std::priority_queue;
const int K = 60;
priority_queue<pii> p;
priority_queue<int> q[K];
int main()
{
int k;
cin >> k;
for (int i = 1; i <= k; ++i)
{
int n;
cin >> n;
for (int j = 1; j <= n; ++j)
{
int a;
cin >> a;
q[i].push(a);
}
}
for (int i = 1; i <= k; ++i)
{
if (q[i].size() > 0)
p.push({q[i].top(), i});
}
while (p.size() >= 3)
{
auto f = p.top();
p.pop();
auto s = p.top();
p.pop();
auto t = p.top();
p.pop();
if (s.first + t.first <= f.first)
{
int id = f.b;
q[id].pop();
if (q[id].size() > 0)
p.push({id, q[id].top()});
}
else
{
cout << f.b << ' ' << f.a << ' ' << s.b << ' ' << s.a << ' ' << t.b << ' ' << t.a << '\n';
return 0;
}
p.push(s);
p.push(t);
}
cout << "NIE" << '\n';
return 0;
}
注意,s组的同志们,我们要掌握一定的二进制写法——zhx
并查集
一个十分美味的算法
主要是路径压缩的优化可以减小并查集的时间复杂度
ps:按秩合并基本没用,按照zhx的话来说,合并时可以用随机合并
P3367 并查集板子AC CODE
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1e6 + 7;
int read()
{
int x = 0, w = 1;
char ch = getchar();
while(ch > '9' || ch < '0')
{
if(ch == '-')
{
w = -1;
ch = getchar();
}
}
while(ch <= '9' && ch >= '0')
{
x = x * 10 + ch - '0';
ch = getchar();
}
return x * w;
}
long long Qmi(int a, int b, int p)
{
if(b == 0)
{
return 1%p;
}
if(b == 1)
{
return a%p;
}
long long ans = Qmi(a, b/2, p);
ans = ans*ans%p;
if(b % 2)
{
ans = ans*a%p;
}
return ans % p;
}
bool isprime(long long x)
{
if(x <= 1)
{
return false;
}
if(x == 2)
{
return true;
}
if(x % 2 == 0)
{
return false;
}
for(int i = 3; i <= sqrt(x); i += 2)
{
if(x % i == 0)
{
return false;
}
}
return true;
}
int n, q;
int to[MAXN];
int go(int p)
{
if(p == to[p])
{
return p;
}
else
{
return go(to[p]);
}
}//连
int main()
{
//freopen("qwq.in", "r", stdin);
//freopen("qwq.out", "w", stdout);
cin>>n>>q;
//先连自己
for(int i = 1; i <= n; i++)
{
to[i] = i;
}
while(q--)
{
int op;
cin>>op;
if(op == 1)
{
int x, y;
cin>>x>>y;
if(rand() % 2)
{
to[go(x)] = go(y);
}
else
{
to[go(x)] = go(y);
}
}
else
{
int x, y;
cin>>x>>y;
if(go(x) == go(y))
{
cout<<"Y"<<'\n';
}
else
{
cout<<"N"<<'\n';
}
}
}
return 0;
}
例2 AC CODE(见pdf)
首先,你要知道,\(n \leq 1e7\)真的会卡掉线段树
于是,我们并查集
int main()
{
cin >> n;
for (int i=1;i<=n;i++)
to[i] = i;
for (int i=m;i>=1;i--)//倒着读 自己实现
{
int l,r,x;
//go(i) 从i向右 第一个没被染色的位置
cin >> l >> r >> x;//第i个操作
int p = go(l);
while (p<=r)//当前位置还在区间内
{
a[p] = x;//染色
int np = go(p+1);
to[p] = go(r+1);
p = np;
}
}
}
伟大的中午
下午力

我们用BFS搜索去找所有点的安全性值,我们再将安全性点从大到小在图里找,如果发现一条路联通了,那么最后加的那个点就一定是最大化的最小值(因为是从大到小找)
Trie树
Trie 树,即字典树,是一种树形结构。典型应用是用于统计和排序大量的字符串前缀来减少查询时间,最大限度地减少无谓的字符串比较
当然,对于Trie的理解,我们可以baidu
01Trie例题

当然,对于01Trie的理解,我们可以baidu加上这张图来理解
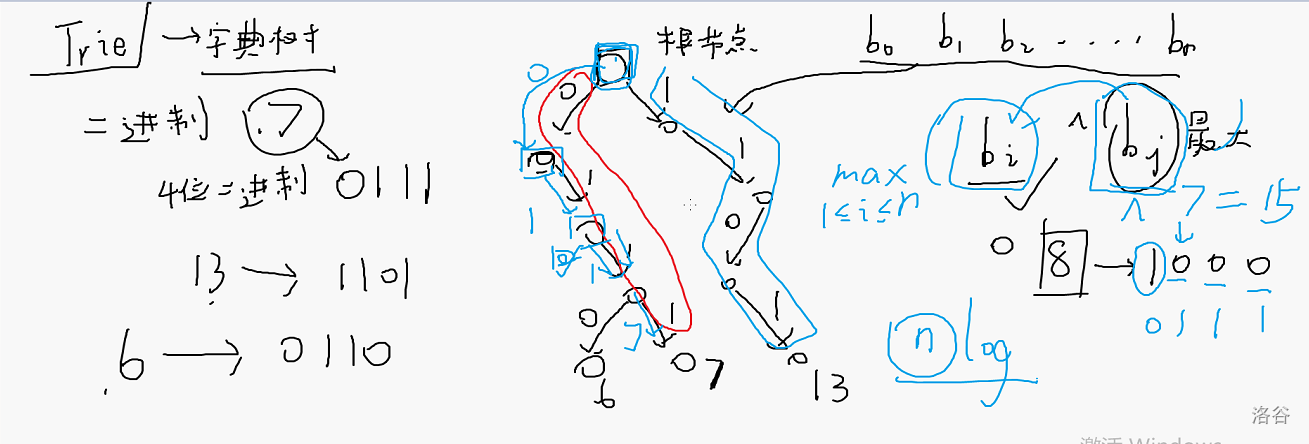
#include <iostream>
struct Node
{
int nxt[2];
Node()
{
nxt[0] = nxt[1] = 0;
}
}z[100010];
int cnt;
int root;
void insert(int x) // 插入一个数
{
int p = root;
for (int i = 30; i >= 0; --i)
{
int y = (x >> i) & 1;
if (z[p].nxt[y] == 0)
{
cnt++;
z[p].nxt[y] = cnt;
}
p = z[p].nxt[y];
}
}
int query(int x) // 查询异或最大值
{
int p = root, ans = 0;
for (int i = 30; i >= 0; --i)
{
int y = (x >> 1) & 1;
if (z[p].nxt[y ^ 1])
ans = ans | (1 << i), p = z[p].nxt[y ^ 1];
else
p = z[p].nxt[y];
}
return ans;
}
int main()
{
root = 1;
return 0;
}
思维

分块
参考baidu
int belong[maxn];//belong[i] 代表第i个数属于第几块
int sum[maxn];//sum[i] 代表第i块的和是多少
int daxiao[maxn];//daxiao[i] 代表第i块的大小是多少
int col[maxn];//col[i] 代表第i块被整体加了col[i]
int main()
{
cin >> n >> m;
for (int i=1;i<=n;i++)
cin >> a[i];
int s = sqrt(n);//每块的大小
for (int i=1;i<=n;i++)
belong[i] = i/s+1;
for (int i=1;i<=n;i++)
{
sum[belong[i]] += a[i];
daxiao[belong[i]] ++;
}
for (int x=1;x<=m;x++)
{
int opt;
cin >> opt;
if (opt == 1)//询问操作
{
int l,r;
cin >> l >> r;
int ans=0;
if (belong[l] == belong[r])
for (int i=l;i<=r;i++)
ans += a[i] + col[belong[i]];
else
{
for (int i=l;belong[i] == belong[l]; i++)
ans += a[i] + col[belong[i]];
for (int i=r;belong[i] == belong[r]; i--)
ans += a[i] + col[belong[i]];
for (int i=belong[l] + 1; i < belong[r]; i++)
ans += sum[i];
}
cout << ans << "\n";
}
else
{
int l,r,v;
cin >> l >> r >> v;
if (belong[l] == belong[r])
for (int i=l;i<=r;i++)
a[i] += v;
else
{
for (int i=l;belong[i] == belong[l]; i++)
a[i] += v,sum[belong[i]] += v;
for (int i=r;belong[i] == belong[r]; i--)
a[i] += v,sum[belong[i]] += v;
for (int i=belong[l] + 1; i < belong[r]; i++)
{
sum[i] += v * daxiao[i];
col[i] += v;
}
}
}
}
return 0;
}
莫队(伟大,无需多言)
莫队,是莫涛发明的一种解决区间查询等问题的离线算法,基于分块思想,复杂度为 \(O(n\sqrt n)\)
主要用于解决无需修改的区间查询问题
莫队思想及过程
1.分块排序优化
将区间划分为 n 个块,对所有查询按左端点所在块排序(同块按右端点排序),并通过奇偶性优化减少指针移动次数
2.双指针暴力转移
维护两个指针L和R,通过逐步移动到目标区间边界,利用相邻区间答案的\(O(1)\)转移特性更新结果,例如统计区间内不同元素数量时增减计数器即可
3.离线处理限制
需预先读取所有查询并排序,无法处理动态修改或强制在线场景,但编码复杂度显著低于线段树等在线数据结构
比较抽象请见this
莫队基本Code
struct query
{
int l,r,id,ans;
}q[maxn];
bool cmp1(const query &q1, const query &q2)
{
if (belong[q1.l] != belong[q2.l]) return belong[q1.l] < belong[q2.l];
else return q1.r < q2.r;
}
bool cmp2(const query &q1, const query &q2)
{
return q1.id < q2.id;
}
void ins(int x)
{
cnt[x] ++;
if (cnt[x] % 2 == 0) ans++;
else if (cnt[x] != 1) ans--;
}
void del(int x)
{
cnt[x] --;
if (cnt[x] != 0)
{
if (cnt[x] % 2 == 0) ans++;
else ans--;
}
}
int main()
{
cin >> n >> m;
for (int i=1;i<=n;i++)
cin >> a[i];
for (int i=1;i<=m;i++)
{
cin >> q[i].l >> q[i].r;
q[i].id = i;
}
int s = sqrt(n);
for (int i=1;i<=n;i++)
belong[i] = i/s+1;
sort(q+1,q+m+1,cmp1);
for (int i=q[1].l;i<=q[1].r;i++)
ins(a[i]);
q[1].ans = ans;
for (int i=2;i<=m;i++)//O(Nsqrt(N))
{
int l1=q[i-1].l,r1=q[i-1].r;
int l2=q[i].l,r2=q[i].r;
if (l1 < l2)
for (int i=l1;i<l2;i++)
del(a[i]);
else
for (int i=l2;i<l1;i++)
ins(a[i]);
if (r1 < r2)
for (int i=r1+1;i<=r2;i++)
ins(a[i]);
else
for (int i=r2+1;i<=r1;i++)
del(a[i]);
q[i].ans = ans;
}
sort(q+1,q+m+1,cmp2);
for (int i=1;i<=m;i++)
cout << q[i].ans << "\n";
return 0;
}
分治
分治算法的基本思想是将一个规模为N的问题分解为K个规模较小的子问题,这些子问题相互独立且与原问题性质相同。求出子问题的解,就可得到原问题的解。即一种分目标完成程序算法,简单问题可用二分法完成
归并求逆序对
void merge(int l,int r)//要计算l~r这个区间有多少个逆序对
{
if (l==r) return;
int m=(l+r) >> 1;//(l+r)/2
merge(l,m);//递归去算l~m的答案 a[l]~a[m] 排好序了
merge(m+1,r);//递归去算m+1~r的答案 a[m+1]~a[r] 排好序了
//i在左边 j在右边的答案
int p1 = l, p2 = m+1;
for (int i=l;i<=r;i++)
{
if (p1 > m) b[i] = a[p2],p2++;
else if (p2 > r) b[i] = a[p1],p1++;
else if (a[p1] <= a[p2]) b[i] = a[p1],p1++;
else b[i] = a[p2],p2++,ans+=m-p1+1;
}
for (int i=l;i<=r;i++)
a[i] = b[i];
}
消消乐
小 L 现在在玩一个低配版本的消消乐,该版本的游戏是一维的,一次也只能消除两个相邻的元素。
现在,他有一个长度为 n 且仅由小写字母构成的字符串。我们称一个字符串是可消除的,当且仅当可以对这个字符串进行若干次操作,使之成为一个空字符串。
其中每次操作可以从字符串中删除两个相邻的相同字符,操作后剩余字符串会拼接在一起。
小 L 想知道,这个字符串的所有非空连续子串中,有多少个是可消除的。
输入格式
输入的第一行包含一个正整数 n,表示字符串的长度。
输入的第二行包含一个长度为 n 且仅由小写字母构成的的字符串,表示题目中询问的字符串。
输出格式
输出一行包含一个整数,表示题目询问的答案。
伟大的思路
看到涉及到整个 \(1-n\) 区间的所有子区间往分治上想。
考虑跨越中间的串有几个可以消。
首先,关于中间对称的可以消。
但 b|aab 也可以消掉。
于是,通过栈来求最简串(无法再消掉的串)
CODE于今晚完成
题单
https://www.luogu.com.cn/problem/P3378
https://www.luogu.com.cn/problem/P1886
https://www.luogu.com.cn/problem/P3528
https://www.luogu.com.cn/problem/P3372
https://www.luogu.com.cn/problem/P3373
https://www.luogu.com.cn/problem/P4113
https://www.luogu.com.cn/problem/P9753
https://www.luogu.com.cn/problem/P3367
https://hydro.ac/p/bzoj-P2054 自行百度题面
https://www.luogu.com.cn/problem/P8306
https://www.luogu.com.cn/problem/P10471
其余见luogu DAY 1题单


 浙公网安备 33010602011771号
浙公网安备 33010602011771号