8月杂题

学习类欧几里得

\(\sum_{x=0}^n\lfloor{\frac{ax+b}{c}\rfloor}\)

• 当 \(a\ge c\) 或 \(b\ge c\) 时，考虑对 \(a\) 与 \(c\) 取模后将其提出。
• 否则，算整点个数可以用长方形点数减去上方个数，而上方点个数可以通过交换横纵轴来计算：\(y=\frac{a}{c}x+\frac{b}{c}\) 交换横纵轴后为 \(y=\frac{c}{a}x-\frac{b}{a}\)。

当然也可以代数推导：\(\sum_{x=0}^n\sum_{i=0}^{\lfloor{\frac{ax+b}{c}\rfloor}-1}1=\sum_{i=0}^{\lfloor{\frac{an+b}{c}\rfloor}-1}\sum_{x=0}^n[i\le \frac{ax+b}{c}-1]\)。后面解个不等式：\(x>\lfloor{\frac{c+ci-b-1}{a}\rfloor}\)。带入原式：\(\sum_{i=0}^{\lfloor{\frac{an+b}{c}\rfloor}-1}(n-\lfloor{\frac{c+ci-b-1}{a}\rfloor})\)，设 \(m=\lfloor{\frac{an+b-1}{c}\rfloor}\)。则有 \(nm-\sum_{i=0}^{m-1}\lfloor{\frac{ci+c-b-1}{a}\rfloor}\)。

记得特判 \(a=0\)。

ARC178D Delete Range Mex

首先注意到两点：删的数字必定递减；若 \(i\) 要被删除，则包括 \([0,i-1]\) 的最小区间必定在 \(o\) 左侧或右侧。

考虑从小到大填入数字，设 \(f(i,l,r)\) 为填入了 \([0,i]\)，其极大区间为 \([l,r]\)，的填入方案数。

SP3871 GCDEX - GCD Extreme

设 \(f(n)=\sum_{i=1}^n\sum_{j=i+1}^n\gcd(i,j)\)，则 \(f(n)-f(n-1)=\sum_{i=1}^n\gcd(i,n)\)。而 \(\sum_{i=1}^n\gcd(i,n)=\sum_{d|n}d\sum_{i=1}^n[\gcd(i,n)=d]=\sum_{d|n}d\sum_{i=1}^{n/d}[\gcd(i,n/d)=1]=\sum_{d|n}d\times \varphi(n/d)\)。线性筛。

P3175 [HAOI2015] 按位或

🔺key：看到“都……的期望步数”，考虑 Min-Max 容斥转为“至少一个……的期望步数”。

题目要求每位都为 \(1\) 的期望步数，相当于求最大值。考虑 Min-Max 容斥，设 \(g_i\) 为集合 \(i\) 中至少一个为 \(1\) 的期望步数。即 \(\frac{1}{\sum_{i\cap j\ne \varnothing} p_j}\)，交不为空可以转换为补集是其子集，就可以用 FWT/高维后缀和。

P4433 [COCI2009-2010#1] ALADIN

区间覆盖，使用线段树维护需要考虑如何快速维护这个函数的区间和。换句话说，我们需要快速求 \(\sum_{i=l}^r(i \times A)\bmod B\)。将取模拆成除法后类欧。

P5605 小 A 与两位神仙

🔺key：\(\delta_ma=\varphi(m)/\gcd(a^\prime,\varphi(m))\)，其中 \(a^\prime\) 满足 \(g^{a^\prime}\equiv a\pmod m\)。\(g\) 为 \(m\) 原根。

和 ABC335G 类似。

取离散对数： \(x^\prime a\equiv y^\prime \pmod{\varphi(m)}\)，即 \(x^\prime a-y^\prime\varphi(m)=b^\prime\)，即 \(b^\prime|\gcd(a^\prime,\varphi(m))\)，即 \(\gcd(b^\prime,\varphi(m))|\gcd(a^\prime,\varphi(m))\)。显然 \(a^\prime\) 和 \(b^\prime\) 无法直接计算，但阶是可以算的，并且 \(\delta_ma=\varphi(m)/\gcd(a^\prime,\varphi(m))\)，所以这相当于判断 \(\delta_ma|\delta_mb\)。

阶的定义：满足 \(a^x\equiv 1\pmod m\) 的最小 \(x\)，成为 \(\delta_ma\)。

阶的计算：先设答案为 \(\varphi(m)\)，那么阶必定是其约数，枚举 \(\varphi(m)\) 的约数并试除，看看除了之后能不能让 \(a\) 的这么多次方还模 \(m\) 等于一。

CF990G GCD Counting

\(\gcd\) 恰好等于 \(k\) 的较为难算，所以可以尝试计算 \(\gcd\) 为 \(k\) 的倍数的路径个数再差分。我们保留所有两端节点编号都为 \(k\) 倍数的边，那么单个连通块内任意路径上点的 \(\gcd\) 都是 \(k\) 倍数，所以我们只需要知道连通块大小，使用并查集即可。复杂度正确性依赖于调和级数。

P4563 [JXOI2018] 守卫

其实挺简单的。

设 \(f(l,r)\) 为能观测 \([l,r]\) 的最小花费。设 \(k\) 为在 \([l,r]\) 内编号最小的 \(r\) 能观测到的位置（注意 \(r\) 不一定能看到 \([k,r]\) 内的所有亭子），则有 \(f(l,r)=\min\{f(l,k),f(l,k-1)\}+f(k+1,r)\)。\(k\) 可以在枚举 \(l\) 时顺便计算出来。

P3177 [HAOI2015] 树上染色

设 \(f(i,j)\) 为子树 \(i\) 内选了 \(j\) 个黑点时的贡献，注意子树 \(i\) 外的黑点个数时已知的，所以可以直接按边拆贡献算出答案。

树形背包 DP 的复杂度正确必须要满足对 \(i\) 子树分配的资源 \(\le siz_i\)，对 \(i\) 以前分配的资源不超过 \(i\) 子树以前子树总大小。这样复杂度就是 \(n^2\) 而不是 \(n^3\)。

P6419 [COCI2014-2015#1] Kamp

车可以不回来，那么我们贪心选择最长链不走。换根 DP 即可。

P5504 [JSOI2011] 柠檬

\(f(i)\) 为 \([1,i]\) 的答案，则有 \(f(i)=\max_{j\in[1,i]\wedge s_j=s_i}f(j-1)+s_i(t_i-t_j+1)^2\)，\(t_i\) 为到 \(i\) 为止与它颜色一致的柠檬个数。显然凸包优化，对每种颜色都开一个单调栈维护。

可以不用二分，因为相同颜色的 \(t\) 单调，故可以走指针。

CF1557C Moamen and XOR

\(\&\) 运算想要在一位上不弱于 \(\oplus\)，那么必须每一位都是 \(1\)。而且如果序列长度为偶数，还能大于 \(\oplus\)，简单计算即可。

P3121 [USACO15FEB] Censoring G

显然把给出的单词建 AC 自动机。然后把文章拿进去搜一下，走到以单词结尾的节点就删掉这个单词。

P3823 [NOI2017] 蚯蚓排队

注意到 \(k\) 比较小，所以每次操作所影响的字符串不多，用双向链表加哈希暴力维护即可。

学习万欧几里得

我们考虑类欧中的线下整点，用一个点从左到右，从下往上依次扫所有整点，往右写一个 R，往上写一个 U。

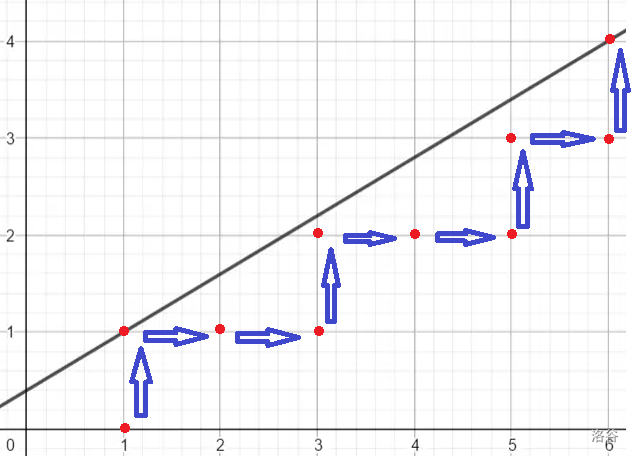
比如这张图片就是 URRURRURU。

那么我们可以把 U 和 R 想象成一个矩阵（其实一般可以不用写成矩阵），每一次的操作就是乘上它。显然我们不能暴力成，故考虑矩阵快速幂的思想：

• \(b\ge c\)：截距不小于 \(1\)，我们就可以把最开始的一些 U 用快速幂合并。

• \(a\ge c\)：斜率不小于 \(1\)，每一次往右都会有增加一定数量的 U，将他们放在后面的 R 即可。

• 否则，我也不会，但可以背一背。

重点还是构造节点与合并方法。

Node F(ll a,ll b,ll c,ll n,Node U,Node R){
    if(!n)return Node();
    if(b>=c)return qpow(U,b/c)*F(a,b%c,c,n,U,R);
    if(a>=c)return F(a%c,b,c,n,U,qpow(U,a/c)*R);
    ll m=((i128)a*n+b)/c;if(!m)return qpow(R,n);
    return qpow(R,(c-b-1)/a)*U*F(c,(c-b-1)%a,a,m-1,R,U)*qpow(R,n-((i128)c*m-b-1)/a);
}

背起来挺容易的。

LOJ6440 万能欧几里得

相当于是想计算 \(\sum A^xB^y\)，考虑合并两个 Node：\(\sum A^{x_1}B^{y_1}\) 与 \(\sum A^{x_2}B^{y_2}\) 合并应该为 \(\sum A^{x_1+x_2}B^{y_1+y_2}=A^{x_1}(\sum A^{x_2}B^{y_2} )B^{y_1}\)，维护 \(A^x,B^y,\sum A^{x}B^{y}\) 即可。

CF1305C Kuroni and Impossible Calculation

🔺key：有模数的题，考虑有可能一些东西模出来为 \(0\)。

当 \(n\le\) 模数时，暴力。当 \(n>\) 模数时，根据抽屉原理，必有两个数模出来同余，相减就变成 \(0\) 了，答案就是 \(0\) 了。

CF919E Congruence Equation

🔺key：有模数的题，考虑循环节。

🔺key：周期 \(a\) 与周期 \(b\) 合并，周期为 \(\frac{ab}{\gcd(a,b)}\)（exCRT）。

\(na^n\equiv b\pmod p\)，\(n\) 的周期为 \(p\)，指数带来的周期为 \(p-1\)（费马小定理），所以 \(na^n\) 的周期就是 \(p(p-1)\)。

设 \(n=i(p-1)+j\)，则有 \((i(p-1)+j)a^{i(p-1)+j}\equiv b\pmod p\)，即 \((j-i)a^{j}\equiv b\pmod p\)，即 \((j-i)\equiv a^{-j}b\pmod p\)，注意到 \(0\le j<p-1\)，枚举 \(j\)，可以算出一个 \(i\) 的特解，从而算出一个 \(n\) 的特解。再根据 \(n\) 循环节为 \(p(p-1)\) 就可以算出解个数。

P3312 [SDOI2014] 数表

假设 \(n=\min(n,m)\)。

若忽略询问的限制，题目所求即：\(\sum_{i=1}^n\sum_{j=1}^m\sigma(\gcd(i,j))\)。这里不写成 \(\sum_{i=1}^n\sum_{j=1}^m\sum_{k|i,k|j}k\)，是因为询问限制是对一类数字的和的限制，拆散了就不好处理了。

\(\sum_{i=1}^n\sum_{j=1}^m\sigma(\gcd(i,j))=\sum_{d=1}^n\sigma(d)\sum_{i=1}^{\lfloor n/d\rfloor}\sum_{j=1}^{\lfloor m/d\rfloor}[\gcd(i,j)=1]=\sum_{d=1}^n\sigma(d)\sum_{k=1}^n\mu(k){\lfloor n/dk\rfloor}{\lfloor m/dk\rfloor}\)。

设 \(T=dk\) 则有：

\(=\sum_{T=1}^n{\lfloor n/T\rfloor}{\lfloor m/T\rfloor}\sum_{d|T}\sigma(d)\mu(T/d)\)

这下就好处理了：设 \(g(T)=\sum_{d|T}\sigma(d)\mu(T/d)\)，将询问离线下来按 \(a\) 排序，每次会让一些 \(\sigma\) 加入下标为它倍数的 \(g\)。询问即数论分块+区间和。用树状数组即可。

BZOJ3853 GCD Array

对 \(x\) 满足 \(\gcd(x,n)=d\) 的位置 \(x\) 加 \(v\)，即对 \(\gcd(x,n/d)=1\) 的 \(xd\) 位置加 \(v\)，即对下标 \(xd\) 加 \(v\sum_{k|x\wedge k|(n/d)}\mu(k)\)。枚举 \(n/d\) 的约数即为 \(k\)，对其倍数加 \(v\times mu(k)\)。

对其倍数加，可以维护一个数组 \(c\)，\(c_i=x\) 意味着下标为 \(i\) 倍数的位置都被加了 \(x\)。询问的时候整除分块一下。\(c\) 数组单点改前缀查用树状数组。

学习杜教筛

为了计算积性函数 \(f\) 的前缀和。我们需要构造 \(g\)，使得 \(g\) 和 \(f*g\) 的前缀和好算，然后：

\(S_{f*g}(n)=\sum_{i=1}^n\sum_{j|i}g_jf_{i/j}=\sum_{j=1}^ng_jS_f(\lfloor n/j\rfloor)=g_1S_f(n)+\sum_{j=2}^ng_jS_f(\lfloor n/j\rfloor)\)

\(f(n)=(S_{f*g}(n)-\sum_{j=2}^ng_jS_f(\lfloor n/j\rfloor))/g_1\)。使用整除分块+记忆化，复杂度 \(O(n^{2/3})\)。

\(\varphi\) 的前缀和构造：\(g=1,f*g=id\)。\(\mu\) 的前缀和构造：\(g=1,f*g=\varepsilon\)。

P3327 [SDOI2015] 约数个数和

反演一波，整除分块套个杜教筛。

LOJ6207 米缇

🔺key：\(\sigma_k(ij)=\sum_{x|i}\sum_{y|j}[\gcd(x,y)=1](\frac{iy}{x})^k\)

化简柿子，最后为 \(\sum_{d=1}^{n}\mu(d)d^k(\sum_{i=1}^{\lfloor n/d\rfloor}i^k\lfloor \frac{n}{id}\rfloor)^2\)。\(\mu\cdot id_k\) 的前缀和可以卷上 \(1\cdot id_k\) 得到 \(id_k\cdot (\mu* 1)=\varepsilon\cdot id_k\)，使用插值可以算出 \(1\cdot id_k\) 的前缀和。使用杜教筛加整除分块即可。

学习 Min25 筛

咕咕咕

LOJ6686 Stupid GCD

首先 \(\lfloor \sqrt[3] i\rfloor\) 一看就非常可以枚举，式子转为 \(\sum_{j=1}^m\sum_{i=j^3}^{\min(n,(j+1)^3-1)}\gcd(i,j)\)，\(\min\) 也可以拆掉：\(=\sum_{j=1}^{m-1}\sum_{i=j^3}^{(j+1)^3-1}\gcd(i,j)+\sum_{i=m^3}^n\gcd(i,m)\)，可以枚举 \(\gcd\) 变成 \(\varphi\) 与整除分块的形式（\(\sum_{i=1}^n\gcd(i,x)=\sum_{d|x}\varphi(d)\lfloor n/d\rfloor\)）。最后我们需要算 \(\varphi\cdot i\) 的前缀和，构造 \(g=id,f*g(n)=\sum_{i|n}\varphi(i)i\times (n/i)=n^2\)。

S15.23.10.2. 涂色

显然可以通过反复横跳来让其中一个合法，相邻的另一个可能不合法。那么一种想法就是先从左到右依次反复横跳，只有最后一个不合法，再从右到左，让第一个不合法，吗？实际上，我们到中途的一个位置就可以停了，这个位置就是目标序列中值差为 \(1\) 的位置！这个位置绝对可以是最后停下来的位置。

S15.23.10.3. 出题

🔺key：对于朴素 DP 式子比较简洁的，考虑动态 DP。

考虑可以先枚举最大值，再通过一次 \(O(n)\) 的 DP，来确定将值不超过 \(lim\) 的元素组合的最大的最小值。

由于最大值一定是某一个数或者与它相邻的数的和。考虑将可能的最大值都列出来（\(2n-1\) 个），从小到大依次加入，每次即在 DP 过程中多增加一个合法的元素，用动态 DP 解决即可。

P3270 [JLOI2016] 成绩比较

恰好 \(K\) 个人被碾压比较困难，尝试容斥，枚举 \(i\) 为至少 \(i\) 个人被碾压。容斥系数为 \((-1)^{i-K}C_i^K\)。再乘上 \(C_{N-1}^i\) 为选出 \(i\) 个人被至少碾压。

对于科目 \(j\)，在没有被碾压的 \(n-1-i\) 个同学中，选出 \(n-R_j-i\) 个同学比 B 神低。知道这门科的排名，就枚举 B 神的分数来算所有人的分数，方案数为 \(\sum_{x=1}^{U_j}x^{n-R_j}(U_j-x)^{R_j-1}\)。二项式展开后插值即可。

P3813 [FJOI2017] 矩阵填数

子矩阵的最大值 恰好为 \(v\) 比较难算，可以转成小于等于 \(v\)。用小于等于 \(v\) 减去小于等于 \(v-1\) 即可。但矩阵之间是有交的，这意味着不能直接这么做，所以容斥就可以了！枚举那些矩阵是算小于等于 \(v\)，那些是小于等于 \(v-1\)。

CF750E New Year and Old Subsequence

设 \(f_{i,0/1/2/3/4}\) 为考虑前 \(i\) 个，选择的串只匹配 \(\varnothing/2/20/201/2017\)，不匹配 \(2016\) 的最小删去字符数，比如只匹配 \(20\) 的意思的，必须要有子序列 \(20\)，也必须不能有子序列 \(201\)。

简单 DP，用线段树维护矩阵转移即可。

P7735 [NOI2021] 轻重边

🔺key：边的限制难做时，考虑化在点上。

可以将操作这么转换：每次将一条路径上所有点染上一种与众不同的颜色。那么重边的定义就变成了：左右端点颜色相同的边。

这样就容易用树剖做了。

P4867 Gty的妹子序列

🔺key：如果想让单点改变成 \(O(1)\)，可以考虑分块。

显然莫队。单点改区间查，用树状数组就要操作与询问都是一次 \(\log\)。但莫队操作数为 \(O(m\sqrt n)\)，询问数为 \(O(m)\)，为了平均复杂度就用分块。

P8969 幻梦 | Dream with Dynamic

🔺key：数据结构维护两种函数的复合，可以观察其值域大小。

\(\text{popcount}\) 函数的值域是 \(\log\) 的，所以我们可以在每一个线段树节点上记一个 \(f\) 数组，\(f_i\) 表示 \(\text{popcount}(x+add)=i\)（\(add\) 为 \(\text{popcount}\) 之前的加法懒标记），这个数在一次 \(\text{popcount}\) 之后会变成什么数字。这样，之后的加法就直接加到 \(f\) 数组上即可。

询问时，只需要找到 \(a_i\) 这个位置的 \(f\) 数组，\(add\) 标记，那么 \(f_{\text{popcount}(a_i+add)}\) 就是答案。

CF620F Xors on Segments

同 P10690。

分块，预处理出 \(s_{i,j}\) 为块 \(i\) 左端点到位置 \(j\) 的答案。询问时在同一块就暴力，否则从左往右依次枚举直到到达下一个块的左端点。暴力枚举时将数字插入可持久化 Trie 即可。

CF1717E Madoka and The Best University

枚举 \(x=\gcd(a,b),y=a+b\)，由于 \(x|y\) 所以调和级数复杂度正确。因此 \(c\) 的值可以确定，\(\text{lcm}(c,x)\) 也能推出。

现在的问题是统计满足条件的 \(a,b\) 对数，即快速计算 \(\sum_{a=1}^{y}[\gcd(a,y-a)=x]\)，即 \(\sum_{a=1}^{y/x}[\gcd(a,y/x-a)=1]\)。根据辗转相减可得其等价于 \(\sum_{a=1}^{y/x}[\gcd(a,y/x)]=1\)，欧拉函数即可。

学习 O1 LCA

先 DFS 一下树，搞出欧拉序，比如是：

\[1,2,3,2,4,2,6,2,1,5,1 \]

那么两个点的 LCA，就是它们两个在欧拉序上第一次出现的位置，的区间里是深度最小值的那个点。比如查询 \(3\) 与 \(6\) 的 LCA，就是查询：

\[1,2,{\color{red}{3}},2,4,2,{\color{red}{6}},2,1,5,1 \]

中的区间深度最小的点，RMQ 即可。

ARC163D Sum of SCC

🔺key：将竞赛图缩点后，得到的形如一条链上加一些与链同向的边。

🔺key：一个竞赛图的 SCC 个数，等于将其点集划分为两个集合 \(A,B\)（\(B\) 非空），且满足 \(A\) 与 \(B\) 之间的连边方向都为 \(A\to B\)，的方案数。

第二个结论的证明：将竞赛图缩点，设其 SCC 有 \(k\) 个，分别为 \(p_1\sim p_k\)，那么划分 \(A,B\) 只能是 \(A=\{p_1\sim p_i\},B=\{p_{i+1}\sim p_k\}\)，而 \(i\) 的取值个数为 \(k\)。

那么就可以 DP 了，设 \(f_{i,j,k}\) 为 \(i\) 个点的完全图，\(A\) 集合有 \(j\) 个点，恰有 \(k\) 条边满足 \(u<v\) 的方案数。每次 DP 时考虑新的点放在 A 集合 还是 B 集合，以及这个集合有多少条边会连向这个点。

P3735 [HAOI2017] 字符串

原题定义的相等相当于 \(\text{LCP}+\text{LCS}+k>\text{len}\)。我们可以强制让中间的区域为 \(k\)，但由于 LCP 和 LCS 可能还会更长导致中间的区域其实 \(<k\)，也就是中间区域 \(<k\) 的被算重了，于是我们可以考虑容斥，减去 \(k\) 为 \(k-1\) 时的答案即可。

对于每一个字符串 \(p\)，枚举其 LCP 长度，同时就可以确定其 LCS 长度。那么我们就要统计有多少个 \(i\)，满足在 \(s\) 中以 \(i\) 为结尾的长度为 LCP 的子串等于 LCP，以 \(i+k\) 开头的长度为 LCS 的子串等于 LCS。

于是我们得出解法：对 \(p\) 建立 AC 自动机，对其反串建立 AC 自动机。而一个 \(i\) 对一个 \(p_j\) 有贡献，相当于 \(s_{1\sim i}\) 在 \(p_j\) 的 fail 树子树中，同时 \(s_{i+k\sim n}\) 的反串在 \(p_j\) 的反串的 fail 树子树中。二维数点即可。

CF468D Tree

好题。

考虑对于每条边，统计出有多少 \((i,p_i)\) 经过了它，显然为这条边左右端点子树大小的较小值，因为我们考虑以重心为根，那么较小值就是深度较大的那一端的子树大小（以重心为根后，任意点的子树大小都不超过 \(n-\) 它的大小），于是每条边都可以卡到这个上限。

称以 \(1\) 为父亲的子树为大子树。

考虑怎么构造字典序最小。每一个点都尝试不是它所属的大子树的其他大子树中的编号最小节点，相当于左节点去匹配右节点，当即将不合法时去匹配一个比较大的右部点；什么时候是即将不合法的时候？考虑 Hall 定理，即将不合法的大子树满足其未匹配的左部点个数 = 不属于它的未匹配的右部点个数，这个时候就必须匹配这个大子树里编号最小的点了。

实现上，开一堆 set 维护每个大子树的未匹配的右部点，以及维护未匹配的左部点个数。

P2943 [USACO09MAR] Cleaning Up G

显然答案最多为 \(n\)，那么在最优的划分中，每一段的数值种类数就一定不超过 \(\sqrt n\)。

那么我们枚举这一段的数值种类数就可以转移了，需要动态维护一个 \(pos_i\) 表示到当前位置数值种类数位 \(i\) 的最左位置，走指针即可。

P3426 [POI2005] SZA-Template

设 \(f_i\) 为前缀 \(i\) 的答案，那么 \(i\) 要么从 \(i-1\) 转移而来，要么从 \(next_i\) 转移而来（\(next_i\) 是 \(i\) 的 Border）。

但后者转移还得有个条件：只用一次长度为 \(f_{next_i}\) 的章，就必须将 \(next_i\sim i\) 覆盖。那么我们存一个 \(g_i\) 表示最考右边的 \(j\) 满足 \(f_j=i\) 即可。

CF1747E List Generation

🔺key：对于序列计数问题，尝试化在二维平面上计数。

可以转换成算二维点的集合大小之和，并且该点集合要存在一条从 \((0,0)\) 到 \((n,m)\) 每次只向右/下的路径穿过它。

钦定这条路径优先往右再往下走，我们可以枚举先右后下的拐点，设为 \(i\)，那么选择方案就为 \(C_n^iC_m^i\)，这样路径的形态就确定了，此时路径上还剩一些点可以选，个数为 \(o=n+m-1-i\)，方案数乘以权值为 \(\sum_{j=0}^oC_o^j(i+j+2)\)。拆拆式子就可以快速计算。

P3242 [HNOI2015] 接水果

考虑一个盘子会接到怎么样的水果。

当盘子的 \(u,v\) 的 LCA 是 \(u\) 或 \(v\)，假设是 \(u\)，那么能接住的水果应满足两个条件：一端在 \(v\) 子树，一端不在 \(u\) 朝 \(v\) 方向的儿子的子树内。LCA 不是 \(u,v\) 同理，那么题目变成了矩阵内点权第 \(k\) 大。可以离线排序一维。用权值线段树套线段树，每次在权值线段树上二分来做到 2log。

注意两个维度不应该混用，所以我们钦定较小的是 \(x\) 维，较大的是 \(y\) 维即可。

P5386 [Cnoi2019] 数字游戏

在值域上做莫队，那么问题转换为单点 \(01\) 修改，区间询问极长 \(1\) 连续段的平方和。

用线段树带 log，考虑平衡复杂度。对序列分块，每一个块建立双向链表，维护 \(1\) 的连续段，询问依次遍历块即可。

操作重 \(0\) 变 \(1\) 容易维护。但当 \(1\) 变 \(0\) 时，双向链表没法知道中间元素的所在连续段的左右端点，所以用不删除莫队即可。

P5071 [Ynoi2015] 此时此刻的光辉

🔺key：一个数的质因子种类数比 \(\log\) 还小得多。

维护区间乘积约数个数，那么就要动态维护区间内每种质因子出现次数，因为一个 \(\le 10^9\) 内的数最多有 \(10\) 种质因子，\(n\) 个数的质因子就是 \(O(10n)\) 的，可以离散化后用桶存储，随后正常莫队。分解质因数需要 Pollard-Rho。

还需要优化：将 \(1000\) 以内的质因数先提出来单独算，这样每个数就只剩下最多两个质因子了，这时再用 Pollard-Rho 就快得多。

P4148 简单题

KDT 模板题，就当作是学习 KDT 吧。

KDT 是平衡树，使用定期重构来平衡。插入时，考虑的维度为滚动，比如第一层先是 \(x\) 维，那么第二层就只考虑 \(y\) 维，第三层就又考虑 \(x\) 维。

类似于线段树，KDT 需要判断询问区间是不是包含了当前区间/与当前区间无交，可以记录子树内每个维度的最大与最小来剪枝。

CF1793F Rebrending

把每个询问的右端点挂在左端点的位置上，从后往前扫，尝试维护一个数组 \(\{x\}\) 表示选择的第二个数字为 \(a_i\) 的答案。

现在的问题在于新加入一个数 \(a_i\) 后数组 \(\{x\}\) 会怎么变化，找出第一个大于等于 \(a_i\) 的数字 \(a_j\)，那么 \(x_j\) 就可以更新为 \(a_j-a_i\)，随后再往后面找第一个大于等于 \(a_i\) 且小于等于 \((a_i+a_j)/2\) 的数 \(a_k\)，那么 \(x_k\) 就可以被更新为 \(a_k-a_i\)，以此类推。

于是我们需要一个单点 chkmin 区间查最小值的线段树来维护 \(\{x\}\)，同时我们还需要动态加元素动态询问值域在某个区间的最小索引，动态开点即可。

CF1178H Stock Exchange

🔺key：对于题目给出的一次函数的东西，考虑可能只有其端点有用。

二分最终时间 \(t\)，可以发现，操作一定是在时刻 \(0\) 时将尽量多的股票换成在 \(t\) 时刻价格大的股票，然后再拿这些股票在 \(t\) 时刻换取 \(n+1\sim 2n\) 的股票。于是第一问完成。

求最少交易次数，发现相当于二分图匹配，于是每个股票往价格小的连边跑费用流，用前缀建图优化即可。

P8985 [北大集训 2021] 魔塔 OL

🔺key：对于询问是某些元素的集合，考虑按 \(\log\) 分块，每次分块预处理出所有情况。

首先询问的东西是一个经典问题，肯定先打最终可以加血的怪，并且按难度从小到大打；再打最终会扣血的怪，按加血从大到小打。那么，我们可以先按这样排序，接下来就是按顺序打了。

但这道题的四维偏序看上去难以维护，故考虑 bitset 那样的方法。按 \(\log\) 来对排完序后的怪兽分块，然后依次考虑每个块，四维偏序的话，可以对时间维排序，对其他维，考虑用桶（其他维值都比较小），这样，对于每个询问我们都能用一个 int 表示出他要打哪些怪兽。

现在的问题在于预处理出任何一个怪兽的集合，按顺序打完这些怪的当前血量和中途最低血量，DP 转移即可。于是，对于每个询问，求出他要打的怪兽的集合后使用预处理出来的值来经行更新（每个询问也要存当前血量与中途最低血量）。

复杂度：\(O(\frac{n}{\log n}(2^{\log n}+q))\)。

AGC005C Tree Restoring

离一个点最远的点必定是直径的某端点。而且容易发现本题种只用考虑直径上的点，因为不在直径上的点，我们只需要把该点挂在直径上对应的点即可满足要求，当然如果限制小于直径一半就没法构造。

现在考虑构造出直径，可以发现 \(a\) 最大的两个一定是直径两端点，而且在直径上从左往右，\(a\) 先变小后变大，开个桶维护。

P2685 [TJOI2012] 桥

可以逆向思考。考虑某一条边，会因为哪些边被删去而成为最短路上的边。

建立出从 \(1\) 开始和 \(n\) 开始的最短路树，并找到一条 \(1\) 到 \(n\) 的最短路链，则考虑每一条不在最短路链上的边 \((u,v)\)，设 \(l_u\) 表示在 \(1\) 最短路树上 \(u\) 与 \(n\) 的 LCA，\(r_u\) 表示在 \(n\) 最短路树上 \(u\) 与 \(1\) 的 LCA，则最短路链上 \(l_u\) 到 \(r_v\) 上某一条边被删去后，最短路都有可能变成 \(1\to l_u\to u\to v\to r_v\to n\)。也就是说删掉这上面某一条边，最短路链就可能会变成 \(1\to l_u\to u\to v\to r_v\to n\)。

需要支持单点 chkmin，找最大值，用线段树维护。

P3761 [TJOI2017] 城市

枚举删去的边，将树断成两棵树，那么新加的边连接的一定是两个树的中点，可以感性理解选择中点，这两颗树的高度都是最小的。

那么现在的问题在于快速维护中点，虽然本题可以直接遍历，但其实存在 \(O(n)\) 的做法。

首先我们删去的边肯定是在原树直径上，那么我们从左往右依次枚举这条直径上的边，即删去的边右移，我们想维护左边一坨的直径长度，只需要遍历新加的树即可，同时左边一坨的中点肯定在原树直径上，走指针即可。

同理处理出从右往左的答案。这样我们再枚举删去的边就能知道左边一坨的中心与右边一坨的中心。

CF1392H ZS Shuffles Cards

称 每一轮 为新的游戏，每一次 为一次抽牌。

注意到每一轮都需要抽到鬼牌才能结束，并且每一轮牌都一样，所以每一轮的期望抽牌量也一样，故答案为 \(E(轮数)\times E(每一轮抽牌数)\)

一张牌被抽中，并且在此之前没抽中鬼的概率为 \(\frac{1}{m+1}\)，故 \(E(每一轮抽牌数)=\frac{n}{m+1}+1\)。

\(E(轮数)\) 的计算，我们可以差分一下，变成

\[E(数字牌全抽中后结束所需轮数)+\sum_{i=1}^nE(还剩i张数字牌没抽到，要抽到一张新数字牌所需轮数) \]

前者显然为 \(1\)，后者就是所需抽的鬼牌数量，可以再多考虑新牌进去，这样抽中新牌或鬼牌的概率就是 \(\frac{i}{m+i}\)，那么期望就是 \(\frac{m+i}{i}\)，因为多考虑了新牌所以还要再减去 \(1\)，最终就是 \(1+\sum_{i=1}^n(\frac{m+i}{i}-1)\)。

P8386 [PA2021] Od deski do deski

好题。

首先要明确一些事实：一个序列 \(S\)，在后面接一个 \(x\)，即 \(S+x\)，还是合法的，那么不管后面又接了什么，比如接了 \(T\) 后可能序列就不合法了，然后我再接一个 \(x\)，就又变成合法了，因为 \(S+x+T+x\) 中我可以把 \(x+T+x\) 消掉变成 \(S\)。

于是考虑 DP，设 \(f_{i,j,0/1}\) 为考虑到第 \(i\) 个，后面可以通过接上 \(j\) 个来变得合法，当前不合法/合法 的方案数，则：

\(f_{i,j,1}\times j\to f_{i+1,j,1}\)，因为我在合法的后面接了一个，还是合法的。

\(f_{i,j,1}\times (m-j)\to f_{i+1,j+1,0}\)，因为我在后面接一个从来没有的数字，虽然现在不合法了，但后面可以接这个新的数字让其合法。

\(f_{i,j,0}\times j\to f_{i+1,j,1}\)，因为我接了一个可以让序列合法的东西。

\(f_{i,j,0}\times (m-j)\to f_{i+1,j,0}\)，我在后面接一个从来没有的数字，让现在不合法了，但这个新的数字在后面接并不能让序列合法，因为最多把后面的东西消成现在这样，但现在这样的序列本来就不合法，所以不会增加 \(j\)。

P2414 [NOI2011] 阿狸的打字机

独立切的 AC 自动机板子题。

按照题意构建出 Trie 树。那么字符串 \(x\) 在 \(y\) 中出现次数，就是 \(y\) 的每个前缀的 fail 节点，属于 \(x\) 子树的次数之和。

于是我们遍历 Trie 树，在 fail 树上做单点改子树查，使用树状数组。

P4765 [CERC2014] The Imp

选物品一定是按照 \(v\) 升序选取，所以先排序，设 \(f_{i,j}\) 为考虑物品 \(i\sim n\)，使用 \(j\) 次魔法，最小收益，则有转移 \(f_{i,j}=\max\{f_{i+1,j},\min(v_i-c_i,f_{i+1,j-1}-c_i)\}\)。前面即考虑买不买这个物品，后面是恶魔考虑要不要使用魔法。

P7114 [NOIP2020] 字符串匹配

枚举 \(AB\) 及其出现周期数，则可以推算出 \(C\)。由于 \(C\) 一定是后缀，所以预处理出每个后缀，出现奇数次的字符数量，统计 \(AB\) 中有多少个前缀的出现奇数次的字符数量比 \(C\) 的少，同样在枚举 \(AB\) 时可以处理出来，复杂度调和级数。

ARC143D Bridges

🔺key：对于一个元素持有两个点的形式，考虑题目相当于将元素拆点，将这两个点看成一个入点一个出点。

对于这道题，将 \(A_i\) 和 \(B_i\) 看作 \(i\) 的入点与出点，入点与出点之间连边后将其看成一个点，那么题目相当于给非树边定向，使得被非树边覆盖的点尽可能多。

那么如果这条非树边是一条返祖边，肯定是希望出点向入点定向，这样返祖时覆盖的点就会更多；否则，肯定是入点向出点定向。

CF1361E James and the Chase

🔺key：遇到题目为统计满足 xxx 的个数，但当满足 xxx 的个数小于某个比例时返回 -1 之类的，考虑可能是随机直到找一个满足 xxx 的东西，再根据其找到所有满足 xxx 的东西。

判一个点是否是好的，有一个简单的判断方法：以它为根进行搜索，查看是否有前向边或横叉边即可。

那么我们考虑随机知道找到一个好点，由于这个好点 \(u\) 到其他点有且仅有一条简单路径并且原图是强连通图，那么我们就可以判断其他点 \(v\) 是否为好点：以 \(u\) 为根建立 DFS 树，首先 \(v\) 的 DFS 树中肯定有返祖边（强连通性），并且不能超过一条（否则就不止一种方案），且指的这个祖先也必须是好点（否则可以沿着这个坏点的路径从而达到不止一种方案）。DFS 解决即可。

CF297E Mystic Carvings

很玄妙的题。

这三条连线可以看作只有以下五种情况：

（题解的图）

显然只有情况二和情况五符合题目要求，所以题目就是求二和五的方案数，可以取补去求一三四的方案数，图一可以枚举一条边，方案就是在其左边相离个数与其右边相离个数的乘积；图二三可以一起看成枚举一条边，另一条边与其相离，第三条与其相交。而某一条边“在其左边相离边个数”与“在其右边相离边个数”可以转换成二维偏序。