7月杂题

CF1458C Latin Square

把矩阵每行/每列变成原来的逆排列，可以看成三维向量 \((i,j,a_{i,j})\) 其中两维的交换。

其余两个操作维护一下偏移量。

P5296 生成树计数

🔺key：和的 \(k\) 次方可以通过 EGF 卷积变为“乘法”。

普通的矩阵树定理只能做【所有生成树边权之积】之和。而注意到 \((a+b)^k=\sum_{i=0}^kC_k^ia^ib^{k-i}\)。于是我们可以用向量的 EGF 卷积来代替乘法。

十三校联考 拆分咒语

首先你先写出一个 DP 式子，然后你猜测它有凸性，故 wqs 二分，你再猜测它决策单调，故用 SMAKE。

但 3log 过不去，考虑 SA 中跳 height 的过程能不能优化成 \(O(1)\)，设 \(x_{i,j}\) 为最初在 \(rk=i\) 的位置，串长为 \(j\) 会跳到哪里。从 \(x_i\) 转移到 \(x_{i+1}\) 相当于后缀覆盖。后缀覆盖单点查，用可持久化分块。

十三校联考 物质鉴定

🔺key：交互题猜序列，考虑分块、二分。

考虑分块，把第一个块的全变成酸，那么后面的块就可以与第一个块进行二分从而得到答案。

十三校联考 对拍

考虑遍历正串的 Trie，动态维护反串的 Trie，每次合并反串的 Trie 时就能统计出答案。

Trie 树合并是不带 log 的。

十三校联考 排列

可以发现，对一个区间做逆排列，相当于在原序列的逆排列中找一段区间，区间加后与原序列的一段区间交换。

单点查、区间交换、区间加。用 FHQTreap 即可。

十三校联考 灌水问题

🔺key：看到与高度有关的信息，可以考虑笛卡尔树。

现算出对于每一个点，淹没完它子树所需要的水量，和淹没它到它父亲所需水量，比如下图绿色就是前者，紫色就是后者。

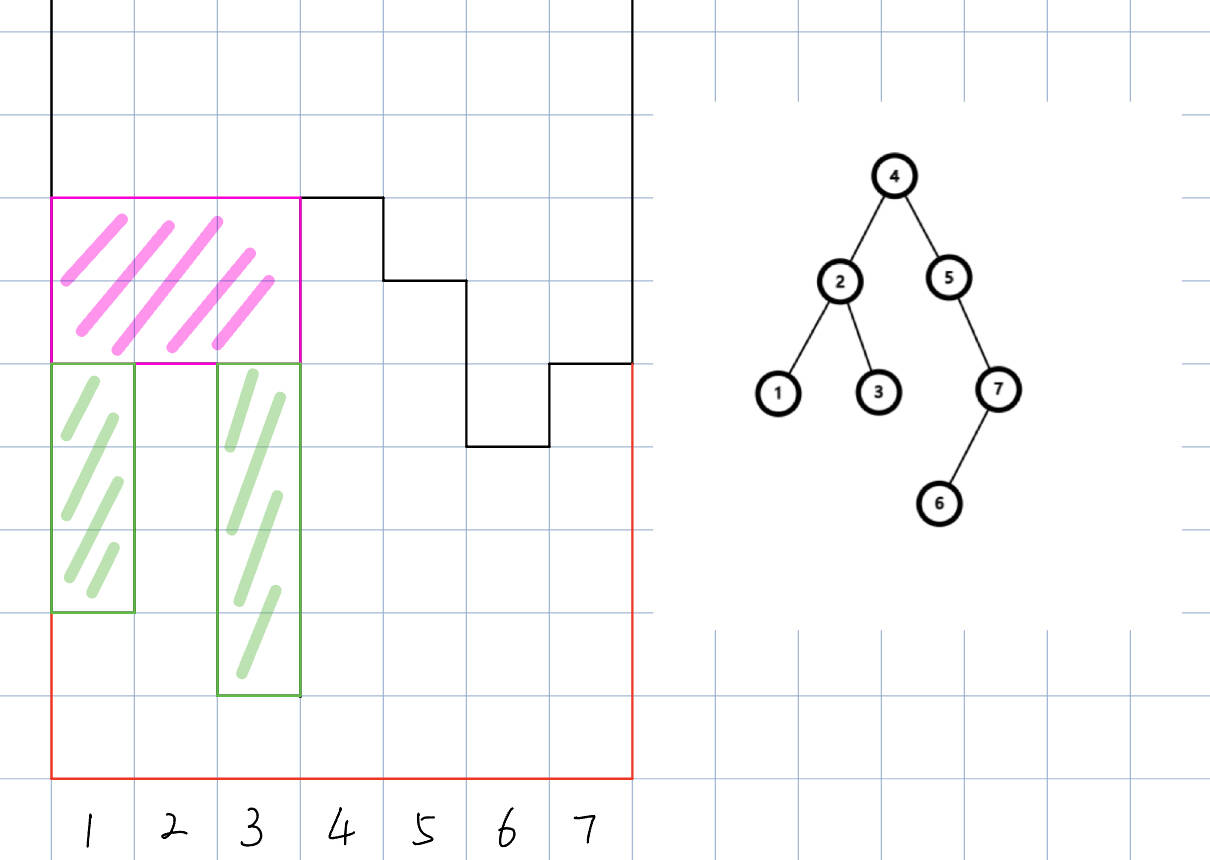
如果一个子树，它是其父亲的左子树，那么父亲淹没它时，会按『后，前，根』的遍历方式；右子树类似。据此可以分类讨论计算答案。

十三校联考 旅游

注意到必有一点，经过它的时刻为 \(0\)。那么这一切都好做了。

设 \(f_{i,j}\) 为从点 \(1\) 开始走到 \(i\)，走 \(j\) 步的最短花费。\(g_{i,j}\) 为在反图上从点 \(n\) 开始走到 \(i\)，走 \(j\) 步的最短花费。枚举那个时刻为 \(0\) 的点，拼在一起即可。

学习 Gale-Shapley

挺简单的一个算法，用于解决稳定婚姻问题。

稳定婚姻问题：一些男人和一些女人，每个男人都有对女人的排名，每个女人亦有，求一组最优秀的匹配。

考虑维护一个落单男人的队列，初始全部落单。每次取出队头并按该男人的眼光枚举每一个女人进行配对，如果这个女人落单，或者这个女人目前对象劣于当前男人，就配对，并将新的落单男人入队，注意当前男人配了对后就 break。

UOJ41 矩阵变换

稳定婚姻练手题。

题目可以看成行与数字的配对。

设 \(p_{i,j}\) 为第 \(i\) 行的数字 \(j\) 所在位置，那么一组解不合法，即存在两行 \(i,j\)，其分别配对的两个数字 \(x,y\)，有 \(p_{i,x}<p_{j,x}<p_{j,y}\)。这启迪我们：行要匹配位置尽量左的数字，数字匹配尽量让它 \(p\) 大的行，用 Gale-Shapley 算法即可。

P5903 树上 K 级祖先

对于树上每个节点，处理出向上的倍增数组。再对树长剖，对链顶记录往上/往下走多少多少个到达的节点。

询问先用倍增数组尽量往上走，再查看所属重链进行查询。

预处理 \(O(n\log n)\)，单次询问 \(O(1)\)。

P3899 更为厉害

\(b\) 是 \(a\) 的祖先的情况是容易统计的。其余情况用 DP：\(f_{i,j}\) 为节点 \(i\) 中，子树内所有与 \(i\) 距离不超过 \(j\) 的节点与 \(i\) 构成的答案。

使用长剖经行优化。注意因为要打一个除了位置 \(0\) 以外的全局加标记，可以在位置 \(0\) 减去这个标记。

P2056 捉迷藏

可以用 LCT 和点分树。但也可以用线段树维护类似区间直径的东西，每次单点改是好做的。

SP16580 QTREE7

反转 \(u\) 的颜色，这个如果直接断掉相邻的边会被菊花卡掉，考虑可以只把它与它父亲的边断掉，询问时求出忽略根的答案（初始时根节点需要有一个额外的父亲），也就是根的右儿子的答案。

这个 trick 非常重要。

P4299 首都

🔺key：两个树连接后，新的树的重心一定在原本两个树的重心的路径上。

根据上面的性质，我们 access 出这条链之后 Splay 上二分即可。

P3703 树点涂色

🔺key：有关将某一节点到根染一种别样的颜色，这一操作可以看成 access。

那么一个节点到根的答案就是沿途上虚链数量 \(+1\)。access 时用线段树维护这个信息。

P5398 GOSICK

🔺key：有关统计互为倍数的问题，算因数直接暴力；算倍数根号分讨，如果这个数 \(>\sqrt V\)，就枚举其倍数，否则，这种数只有 \(\sqrt V\) 种，离线下来枚举这个数，一起算有关它的询问。

这个 trick 在由乃的玉米田里也有。

P4509 葱

🔺key：对于答案数量有保证的题，完美剪枝是可行的（即：只要往下搜就当且仅当一定至少有一个答案可以被搜到）。

考虑判交问题，可以用如下方法判：如果这个线段两个交点分别在直线一左一右就有交。判左右可以将点 \((x,y)\) 代入到直线解析式中 \(Ax+By+C\) 判正负。

我们用 Treap 维护一下最大值/最小值，每次递归时检查将最值的几种组合带入是否为不同号，不同号就说明必定有交，递归即可。复杂度因为题目保证答案不超过 \(10^6\) 故正确。

P6072 Path

🔺key：选择两条不相交路径，可以枚举每一个点，在其子树外找一条路径，子树内找一条路径来形成一组可能的答案。

设 \(a_x\) 为节点 \(x\) 到根的异或值。按照上面的 trick，子树内的问题可以用启发式合并：每次深搜较小的 Trie 的所有值，放到较大的里面询问并插入。

子树外，考虑求出 \(p,q\) 使得 \(a_p\oplus a_q\) 最大，那么不以这个值为子树外的答案的肯定就是 \(p\) 到根链上所有节点和 \(q\) 到根链上所有节点，直接搜一遍建出 Trie 就可以求出。

CF1995B2 Bouquet (Hard Version)

我怎么连 Div2B2 都不会了。

显然我们用值为 \(x\) 的填到尽量多，如果还能填就用 \(x+1\)。这还不够，此时可能会剩下一些 \(x+1\)，我们用剩下的 \(x+1\) 去替换用过的 \(x\)，这显然就是能换多少换多少吧。

CF1995C Squaring

一个很直接的想法就是对于每个数求出至少平方多少次才能超越前面的数，再做一遍前缀和。这显然是错的，比如 \([4,2,4]\)，\(2\) 需要做一遍，但最后的 \(4\) 其实压根不需要跟着平方，我们不需要让这个数跟着做和前面一样多的操作，那么每次我们就减去多算的部分：它可以省去前面那一个数追上它的次数。

CF1996G Penacony

这道题最关键的地方在于，当我们固定一条边必须是不修复的，那么所有覆盖都能确定方案。

所以我们一次枚举这条边，用线段树简单维护。

CF1995D Cases

🔺key：划分子串，子串长度不得超过 \(k\)，可以认为原串中所有长度为 \(k\) 的串中都有划分的结尾。

设 \(T_i\) 为原串中 \([i,i+k-1]\) 中出现字母组成的集合。那么我们相当于是想找一个大小最小的集合 \(S\)，使得每个 \(T_i\) 都与 \(S\) 有交。

转换一下就是，使得每个 \(U-T_i\) 及其子集都不是 \(S\)。于是给 \(U-T_i\) 及其子集都打上标记，使用高位前缀和。最后求出没标记的大小最小的集合。

ABC364F Range Connect MST

🔺key：看到最小生成树不要总是想 Bruvka，可以思考一下模拟 Kruskal 和 Prim。

考虑 Kruskal 算法。先将边排序。现在要解决的问题是快速枚举一个区间里不连通的块并合并。注意这是均摊的所以直接用并查集做。

ABC352G Socks 3

\(p_i\) 为第 \(i\) 次及以后才抽到相同颜色的概率。则答案为 \(\sum p_i\)。

\(p_i\) 也相当于是前 \(i-1\) 没抽到相同的概率，则有 \(p_{i+1}=\frac{\sum_\limits{b_1\cdots b_i}\prod_\limits{j\in[1,i]} a_{b_j}}{C_{\sum a}^i}\)，上面意思是选择 \(i\) 种袜子，每种袜子选一个，第 \(i\) 种袜子的生成函数就是 \(1+a_ix\)，用 NTT 卷积。

ARC180D Division into 3

可以分讨最大值在左中右哪一段，在中间是简单的，在右边与在左边对称。最大值在左边，设其在位置 \(x\)，那么相当于找 \(\min_{i\in[x+1,r]}a_i+\max\{a_{i+1}\sim a_r\}\)，因为在中间这一段的肯定只有一个数。

解决这个问题可以对 \(r\) 扫描线，设 \(f_i=a_i+\max\{a_{i+1}\sim a_r\}\)，用线段树动态维护 \(f\) 数组即可。

ABC356G Freestyle

🔺key：看到两个属性，考虑画到平面上。

对于两种姿势 \((A1,B1)\) 和 \((A2,B2)\)，其组合也可以看成一种姿势，而这相当于是两点之间的连线，所以将题目中的姿势画到平面上，其连线也是合法的姿势，而两个姿势一个严格强于另一个，那么后者可以忽视，据此我们可以构成一个凸包。

询问相当于求一条射线与凸包的交点，使用二分解决。

ABC340G Leaf Color

🔺key：看到计算“颜色均一致”，考虑枚举这个颜色。

考虑枚举叶节点颜色，这样所有节点颜色均可视为 \(0/1\)（相同/不同）。

DP。设 \(f_i\) 为考虑只在节点 \(i\) 的子树里，其选择的叶子颜色均为 \(1\)，且必须选 \(i\) 的方案数。对颜色为 \(1\) 的节点建虚树经行转移即可。

ABC335G Discrete Logarithm Problems

🔺key：一个数的离散对数难算，考虑计算离散对数与 \(\phi(P)\) 的 \(\gcd\)，差不多就是阶。

\(A_i^k\equiv A_j\pmod P\)。设 \(g\) 为原根，\(A_i\equiv g^x\)，\(A_j\equiv g^y\)，则有 \(xk\equiv y\pmod {\phi(P)}\)，即 \(xk-\phi(P)t=y\)。根据贝祖有 \(y|\gcd(x,\phi(P))\)，推出 \(\gcd(y,\phi(P))|\gcd(x,\phi(P))\)，转换成求阶，虽然我们无法求出 \(x\) 与 \(y\)，但阶可以通过枚举 \(\phi(P)\) 因子求出。然后本题就转换成统计倍数二元组个数了。

ABC332G Not Too Many Balls

🔺key：最大流=最小割，考虑写出最小割式子并化简

可以建出最大流模型，随后考虑其最小割怎么算。由于这张图类似于二分图，所以最小割式子容易写出。化简后一个是背包一个是分段函数。

ABC329G Delivery on Tree

遍历方式一定时 DFS。拿起一个节点的球时一定是要离开该点的时候，放下则是刚进入这个点。遍历时的儿子顺序是问题的关键，比如终点有一个兄弟，我们可以带着球先遍历其兄弟，也可以到该点放下球遍历完后再遍历其兄弟。

设 \(a_i\) 为如果节点 \(i\) 比其兄弟更先遍历，那么其会对兄弟多造成多少。\(b_i\) 为后遍历会对兄弟多造成多少。随后 DP 即可。

ABC328G Cut and Reorder

容易发现操作一最多经行一次，并且总可以在最后才执行。

设 \(f_S\) 为将序列 \(a\) 的前 \(|S|\) 个放到序列 \(b\) 种位置集合为 \(S\)。最小代价。每次枚举再往后划一段多长的区间。

ABC327G Many Good Tuple Problems

题目即 \(n\) 个点 \(m\) 条边（可有重边）的有标号二分图计数。

\(F_{i,j}\) 为 \(n\) 点 \(m\) 条边无重边的带标二分图个数（左部点与右部点区分），转移枚举左部点个数即可。

左部点与右部点区分，指若一张图左部点为 \(1,2,3\)，右为 \(4,5\)。那么其与左部点为 \(4,5\)，右为 \(1,2,3\) 不一样，即使图完全一致。

\(G_{i,j}\) 为 \(n\) 点 \(m\) 条边无重边的连通带标二分图个数（左部点与右部点区分），转移枚举节点 \(1\) 所属连通块点数与边数。

这里搞成连通图，是为了解决左部点与右部点区分的问题，连通二分图只有两种染色方案，故除以二就是不区分的答案。

\(H_{i,j}\) 为 \(n\) 点 \(m\) 条边无重边的带标二分图个数（左部点与右部点不区分）。同样枚举连通块 \(1\) 点数与边数。

重边的情况。枚举去重后的边个数并容斥。

ABC326G Unlock Achievement

等级上限很小，故直接最小割。

ABC324G Generate Arrays

任意一号序列均可描述成 在原序列中，下标范围在 \([l,r]\)，值在 \([L,R]\) 的元素顺次构成的序列。

问序列长度直接使用主席树。操作二直接修改 \(L,R\)，操作一需要二分下标刚好大于 \(x\) 的元素在哪。毕竟我们不能直接得出序列长度等信息，需要询问主席树。

ARC179D Portable Gate

令棋子初始位置为根，考虑根固定的情况。设 \(f_{i,0/1}\) 为遍历完 \(i\) 子树不要/要返回 \(i\) 的最小操作数。不用返回则贪心地不返回最长链。

根不固定就换根，写起来比较麻烦。