6月杂题
CF1943D2 Counting Is Fun (Hard Version)
🔺key:对于一段区间集体减,大多可以转换成只考虑其与相邻数的关系。
序列合法的条件可以转换为 \(a_i\le a_{i-1}+a_{i+1}\),随后使用容斥 DP,钦定哪些地方是不满足哪些条件的,转移时记录转移到了位置 \(i\),\(a_i\) 的值,钦定的不合法的个数的奇偶性。
🔺key:对手是随机怪的“博弈”,策略往往也是乱做(毕竟不知道对方的策略),因为是乱做所以不如钦定每次就选最靠左的 xxx,这样策略就不带随机因数了。
Snuke 的策略其实很简单,从左往右按每个开关,如果 \(i=p_i\),就死了,否则把这整个置换都按出来。
所以让 Snuke 赢的排列就应该满足:令 \(t\) 为从左往右第一个满足 \(t=p_t\) 的,前 \(a\) 个没有满足的则 \(t=a+1\),那么 \(p_i(i\in[a+1,n])\) 要满足其所在的置换要存在一编号 \(\le t-1\)。枚举 \(t\),前 \(t-1\) 要错排,容斥枚举钦定 \(i\) 个是对排的加个组合数和容斥系数,计数排列问题即可。
🔺key:遇到既有 \(<\) 的限制,也有 \(>\) 的限制,可以将 \(>\) 容斥成 \(\le\) 和无限制。
按上面的方法容斥,无限制的点把序列分成若干段,若干段之间用生成函数卷起来。块内的方案数可以用整数划分数那样的 DP(实际上就是我不太会 \kk)
🔺key:mex 即不在其中的元素的 min,可以转换。
🔺key:树上特殊的序列,可以考虑前/中/后遍历,dfn 序,euler 序。更重要的,dfn 序还分【入 dfn 序】,以及【出 dfn 序】。
这两个序列就是 dfn 序列的入与出两个版本了。我们可以问出不在这条链上最小值,而“不在一条链的点”就可以通过这两种序列拆出。
🔺key:询问有关位运算,考虑拆位
🔺key:一个序列的本质不同的前缀或只有 \(O(\log V)\) 个,因为每一次或值的增加都是增加一处 \(1\),总共只会增加 log 个 \(1\)。
使用线段树,每个节点暴力存下每种前缀按位或的变化点(有点类似存储分段函数),只会存下 log 个。pushup 时需要计算左端点在左区间,右端点在右区间的答案,直接枚举是 log 方的,因为按位或有单调性,所以可以在这 log 个值上走指针:固定一个左端点 \(l\),走指针出最近的 \(r\) 使得 \(l\sim r\) 的或值 \(\ge v\)。
CF1936E Yet Yet Another Permutation Problem
🔺key:遇到统计每一项都不满足 xxxx 的,考虑容斥。
考虑容斥,钦定一些地方是相同的。
以 \(a_i\) 分段(\(a_i=\max_{j\le i} p_j\)),设第 \(i\) 个所在段的上一个段的最后一个位置为 \(las_i\)。设 \(f_i\) 为考虑到位置 \(i\),且最后一个被钦定。
\(f_i=-\sum_{j=1}^{las_i-1}f_j\frac{(a_i-1-j)!}{(a_i-i)!}\times \left\{\begin{matrix} (i-j)&a_i\ne a_{i-1} \\ 1&a_i=a_{i-1} \end{matrix}\right.\)
分治 NTT 即可。
🔺key:平面图性质:当 \(|V|\ge 3\),则有:\(|E|\le 3|V|-6\)。
🔺key:平面图的团可以直接搜,因为团大小不超过 \(4\),方法是每次取出度数最小的(度数不超过 \(4\)),找与其相邻的,随后暴力找团,再删掉它,用优先队列维护度数最小的点。
由于答案至少是 \(0\),又根据上面的信息以及题目中平方后又乘大常数的式子,所以不难得 \(|S|\le 6\)。
\(|S|=6\) 的情况,我们可以删去度数最小的点,因为其度数上限为 \(4\),加上它是不优的。
\(|S|\le 5\) 的情况,要么选一个团,要么缺失一条边。搜出所有团,方法:选取度数最小的点,然后搜与其连边的,同时把这个点删掉。复杂度是 \(O(n\log n)\) 的,因为度数最小的度数 \(\le 5\),故复杂度正确,用优先队列维护度数最小的点。
CF1920F2 Smooth Sailing (Hard Version)
🔺key:判断一个点是否在一个闭合回路内,可以从这个点向任意方向引一条射线,若不考虑相切,那么和回路的交点为奇数时这个点在回路内部,否则在外部。
先算出每个点权值:与其最近火山距离。根据上面的 trick,将岛屿引一条射线出去,再拆点,每个点拆成两个点:经过这条线奇/偶次。现在就是找一条从 \((x,y)\) 到 \((x,y)^\prime\) 的路径使得路上权值最大值最小。用 Kruskal 重构树或者整体二分皆可解决。
若球要从 \(A\) 移向 \(B\),就把 \(A\) 到 \(B\) 连一条有向边。考虑 \(C\) 都 \(=1\) 的情况,显然每个连通块是相互独立的,一个连通块是可以自己直接流动的,当且仅当 \(|V|=1\) 或存在一点度数 \(>1\)。
现在考虑普遍情况。一个连通块就可以帮助别的没法流动的连通块。按照上面,可以将边分四类:\(A_i\) 等于/不等于 \(B_i\),在/不在一个存在度数 \(>1\) 的连通块中。分类讨论计算代价。
🔺key:到达某个点的期望步数,可以先算出每个点被途中经过的概率,相加就是答案。(如果每个点只会最多被经过一次的话)
在左边界和上边界的点被经过的概率是可以直接暴力算出的,对于其他点,有 \(P(x,y)= \frac{2}{(x+y)(x+y-1)}\)。枚举 \(x+y\),计算有多少点 \((x,y)\) 满足 \(xy\ge k\) 且 \(x+y\) 是我们枚举的,解个二次方程即可。
🔺key:“相邻两项的关系”、“区间加”,可以想到维护差分序列。
🔺key:用 set 维护区间比较麻烦,不如维护断点。
矩阵是无用的,容易简化成统计 \(a\) 与 \(b\) 长度相同、且在 \(a\) 中是相邻不同,在 \(b\) 中也是相邻不同的子区间对数。维护差分序列,再维护 \(a\) 与 \(b\) 各自的极长的满足条件的区间,用 set 维护断点(差分值为 \(0\) 的位置)。
\(a\) 中一个长度为 \(x\) 极长区间与 \(b\) 中一个长度为 \(y\) 极长区间,会给答案带来 \(f(x,y)=\sum_{i=1}^x(x-i+1)(y-i+1)\)(假设 \(x\le y\)),答案即 \(\sum\sum f(x,y)\)。可以推式子变成动态一维带权数点,用树状数组维护。
🔺key:对于题目是给定不同操作问最优操作策略,可能有 最优操作下不同操作之间顺序固定、次数固定 等性质。
不难观察出二操作只会最后用且只用一次,可以算出不用翻转的最优策略,即每次将最低位的零与最高位的一交换;用翻转,我们一定是固定一个区间,将区间外的 \(1\) 全部换到区间的一段连续高位段,然后再翻转;
注意需要先最小化区间长度 \(l\)(题目要求数值最小,与字典序有差异:前者先比较长度),\(l\) 容易计算;再考虑字典序的问题,可以前缀排序,按排名从小到大枚举区间起点,往外延申 \(l\) 到区间终点,判断区间是否合法(即是否可以把区间外的一都移进来),合法的话就是答案。
CF1919F2 Wine Factory (Hard Version)
🔺key:对于网络流,观察其是否是平面图。
可以网络流,建出的图是平面图,转换成求对偶图最短路,由于有拓扑序,转成 DP 方程,再用矩阵支持修改。
也可以分块,先不考虑前面的块带来的水,可以考虑一个独立的块能产生多少酒、最终流出多少水、如果有前面块的支援还能将多少水转换成酒,最后的东西是为了计算前面的块流出的水能让这一块多产生多少水,前面留来的水与这个取个最小值,就是能多产 生的酒。三者都是扫一遍能做的,答案计算也是简单的。
🔺key:看到 \(\pm 2\) 等信息,考虑奇偶分类讨论。
\(x\) 向 \(x-2\) 与 \(x+k\) 连边,问题转换为选一个点集使得无环。\(k\) 为偶数好做,图是两条链;为奇数时,环只有可能是两个倒三角相拼,注意到环大小为 \(k+2\),直接 DP,记下两边长度。
AGC032F One Third
🔺key:在 \([0,1)\) 上随机选取 \(n-1\) 个点,分成的 \(n\) 条线段中,第 \(k\) 短的长度期望为 \(\frac{1}{n}(\frac{1}{n}+\frac{1}{n-1}+\cdots+\frac{1}{n-k+1})\)。
令切的线为白线,一条白线左转 \(\frac{2}{3}\pi\) 出一条红线,右转出一条蓝线,题目就变成选两条不同色的线使得夹角最小,放在数轴上即在 \([0,\frac{2}{3}\pi)\) 上随 \(n-1\) 个点,每个点随机三染色,问两段不同色的最短线段长度的期望。
枚举 \(k\) 表示两段不同色的最短线段是第几短,那么前 \(k-1\) 条就必须两端同色,可以算出这样的概率是 \((\frac{1}{3^{k-1}}-\frac{1}{3^k})\frac{1}{3}\),再套用上面的 trick 即可。
🔺key:观察 SG 函数的形式有助于对其优化。
先暴力 SG 函数,设 \((x,y)\) 为 \((i,j)\) 的后继黑点,则有 \(SG(i,j)=\text{mex}\{\oplus SG(x,y)\}\),而在边缘上的 SG 为 \(1\),故有 \(SG(i,j)=\{\oplus SG(x,y)\}\oplus 1\),可以得出 SG 能被拆成二维前缀异或和,设 \(S(i,j)=\oplus_{x\le i}\oplus_{y\le j}SG(x,y)\),则有 \(S(i,j)=S(i,j-i)\oplus 1\),用辗转相除再差分即可算出 SG。
枚举根,再对于每个点,要将子树中所有棋子转到这个点,需要多少次外援的步数,可以算出一个上界和下界,上界即每个儿子的上界加上儿子子树的棋子数量和,下界的话可以找出儿子中最需要帮助的,计算差即需要外援的。最终根节点的下界必须为 \(0\)。
🔺key:“恰好”难算,转换为算“钦定”。
考虑什么情况下序列不同但矩阵相同,只有可能是有一处拐点,使得两种不同的序列对应同一种矩阵,且如果 \((x,y)\) 有一处拐点,那么 \(x\) 行和 \(y\) 列不会有其他的拐点。
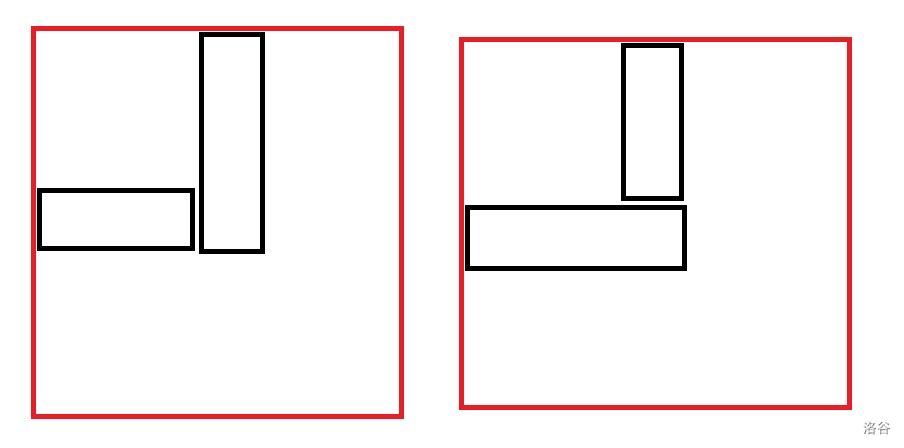
倘若我们算出恰好 \(i\) 个拐点的序列方案数 \(g_i\),答案就是 \(\sum \frac{g_i}{2^i}\)。先算钦定 \(i\) 个拐点的矩阵方案数 \(f_i\),再得出钦定 \(i\) 个拐点的序列方案数 \(h_i\),最终得出 \(h_i=\sum_{j\ge i}g_jC_j^i\),反演一下再带入答案中化简。
🔺key:对 \(01\) 序列的变换,可以在相邻不同处画杆子。
在 \(01\) 之间放一个蓝杆,在 \(10\) 之间放一个红杆,改变一个 \(0/1\) 就是将杆子右移/左移一位,而不能连续出现三个相同的,就是杆子不能相撞!现在的问题就是将初始杆子于结束杆子匹配,使得匹配的杆子距离之和最小,枚举第一个杆子匹配哪一个,剩下的可以依次确定。
AGC030F Permutation and Minimum
🔺key:计数问题考虑转换成更好处理的条件,比如变成匹配计数。
问题可以转成将 \(1\cdots 2\times n\) 的数给连线匹配。故可以从大到小 DP:\(f_{i,j,k}\) 为考虑完 \([i,2\times n]\) 的数,有 \(j+k\) 个数没匹配左端点,其中有 \(j\) 个数在原序列出现过,\(k\) 个没有,转移时考虑是否取一个留着的数进行匹配,还是留着让更小的数匹配它。注意出现过的不能和出现过的进行匹配。
🔺key:解其中某一项应恒等于常数的方程组,可以观察方程的性质,比如可以整体加常数。
容易列出期望方程,再转成异或卷积(因为 \(E_0=0\) 所以还要减去一个常数,可以解得该常数为 \(2^n\)),FWT 后变成对位相除后再逆回来。
注意 \(E_0\) 应当等于 \(0\),而逆回来后不一定,但观察原 DP 式可以得到答案整体加一个常数是不影响的,故将答案整体平移即可。
🔺key:对于限定次数的构造题,可以观察限定的此数有什么特点,从而反推出性质。
\(\lfloor \frac{n}{6}\rfloor\) 提示我们每个数只能操作一次,并且只用操作其中的后一半。
考虑每次拿 \(3\) 个数,使得取 \(\text{lcm}\) 后可以两两 \(\gcd\) 表示出另一个。构造方法:设剩下的数字个数为 \(m\),当 \(m\) 为奇数时可以拿 \(m-2,m-1,m\);\(m\mod 4=0\) 时拿 \(\frac{m-2}{2},m-1,m\);否则 \(m-2,m-1,\frac{m}{2}\)。
CF1930G Prefix Max Set Counting
🔺key:对于两点的贡献,可以拆贡献,其中一个点将其贡献挂在祖先上,再用数据结构维护。
设 \(f_i\) 为以 \(i\) 结尾的前缀最大序列个数,则有 \(f_i=\sum\limits_{i可接在j后}f_j\),现在要快速找出合法 \(j\) 的 \(f\) 和。\(j\) 是 \(i\) 祖先时,是好找的(最多一个);再统计不是祖先的,考虑 \(i\) 与 \(j\) 的 LCA,LCA 到 \(i\) 的编号都不大于 \(i\),故可以倍增找出最浅 LCA。将 \(j\) 的贡献落到其祖先上即可直接统计。
十三校联考 徽章交换
🔺key:当操作之间有时序关系时,将操作看成点,按时序连边。
操作的时序比较麻烦,可以考虑将操作看成点,按时序连边,现在要选出若干条路径,但点不能相交,这样问题就转换为不相交路径但要求选出的权和尽量大。
考虑 LGV 引理,给每条边随机赋权,选出互相之间线性无关的且权和最大,使用实数线性集。
十三校联考 可可
🔺key:当导致结果算重的点构成联通块时,因为点数-边数=1,所以考虑点边容斥。
一个很 navie 的想法是对于每个点 \(x\),用淀粉质算出离它不超过 \(k\) 的点个数,在其中选 \(m\) 个再相加,但这样显然会算重。
发现如果一个相同的 \(m\) 个点的点集,其 \(x\) 必定组成一个联通块,而我们希望它只被计算一次,考虑边点容斥:减去每一条边的答案。定义一条边的答案为到它两端距离都不超过 \(k\) 的点个数,这个是好算的。
十三校联考 前奏
神秘找规律题。
十三校联考 异或
🔺key:异或问题,考虑 01Trie 上 DP。
建出 01Trie,考虑 DP:\(f(x,y)\) 为在子树 \(x\) 和子树 \(y\) 中选点,最多能选多少点,因为 \(x,y\) 深度必须一致所以状态数有保证,每次分类讨论 \(k\) 在当前深度这一位是 \(0\) 还是 \(1\) 进行转移。
带修,每次只会修改两条链上的答案,所以直接做。
十三校联考 魔法阵
🔺key:看到对于不等式组的最大化/最小化问题,考虑其对偶问题。
转换成对偶问题后容易列出简洁的 DP 方程,用 KTT 维护。
十三校联考 小清新字符串题
🔺key:看到复制串,可以考虑优秀的拆分:枚举 \(len\),每 \(len\) 个放一个哨兵,则长度为 \(len\) 的复制串必定经过两个哨兵,所以查看相邻的哨兵,算出前缀的 LCS,后缀的 LCP。
先跑一遍优秀的拆分。算出每一等价类的复制串的开头集合和结尾集合。询问相当于计算开头和结尾都在 \([L,R]\) 之间的复制串,需要一点小容斥。

用线段树维护。
十三校联考 倍杀出题者
在 SAM 上跑一遍:动态移动两个指针 \(x\) 和 \(y\) 一个指针的移动速度恰好是另一个的两倍,这样给答案加上 \(cnt_x\times cnt_y\) 即可。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号