5月杂题
CF1970G3 Min-Fund Prison (Hard)
🔺key:分集合,考虑背包+bitset 优化
添加的边肯定是固定的,为连通块个数 \(-1\)。跑个边双,问题转换成给一些数,可以把其中一个数分裂成两个(这两个数之和为原数),再分成两个集合 \(A,B\),使得集合 \(A\) 的权和的平方加 \(B\) 权和的平方最小。
可以用背包 DP 出第一个集合 \(A\) 的权和,设 \(f_i\) 为集合 \(A\) 的权和为 \(i\) 是否可行,用 bitset 加速。
🔺key:树是二分图,所以最大匹配是最小点覆盖。
于是枚举最小点覆盖集合,这样就能确定选了哪些边了(选的边的端点至少要有一个在点覆盖集合中)。
拿这些边跑一个 Kruskal,如果选的边少于 \(n-1\) 那这个点覆盖就不合法,否则取最小值就是答案。
🔺key:对于为积和形式的矩阵,可以将其分解再利用结合律“缩小”矩阵。
DP:\(f(i,u)\) 为到了第 \(i\) 天,走到叶子 \(u\) 的方案数。
考虑优化。
设 \(w_u=s_u+l_u\),则有:
写出其转移矩阵
注意到转移矩阵有:
换元:
于是答案为:\(A^n=(BC)^n=B(CB)^{n-1}C\)。
最后一次矩阵乘法只用算第一列不然会炸。
CF1970B3 Exact Neighbours (Hard)
🔺key:对于构造题,可以先分类讨论显而易见的情况。
构造题。
如果存在 \(a_i=0\) 的,说明这个房子放哪都可以。那么把 \(a_i=0\) 的放在左上角,其余的按 \(a\) 从大到小排序,排成一个堆之字型,每一个房子都指向前面一个。
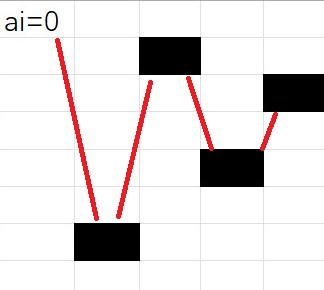
如果存在 \(a\) 相等的一对,把它们放在左边两列形成互相依赖,并且第二个在第二列的第一行。剩下的也排序后按之字型。
否则,\(a\) 是一个 \(1\sim n\) 的排列。排序后前面的按之字型,每一个都指向后面一个,剩下的 \(1,2,3\) 可以简单构造让它们互相依赖。
CF1970A3 Balanced Unshuffle (Hard)
🔺key:如果题目定义了一种变换,现在给出结果序列要求复原,可以考虑某些在被变换序列的东西上放在结果序列上有什么特征。
尝试复原出每一个括号在原括号序列的不平衡值。
将给出的括号序列分段,每一段的不平衡值相同。设在第 \(i-1\) 段的左括号数个数为 \(s\),那么第 \(i\) 段的右边应该尽量往右伸知道包含超过 \(s\) 个右括号。
知道不平衡值就可以复原出原序列了。因为题目有排序后的性质,所以简单完成。
🔺key:对于要让序列满足任意子区间都满足xx条件,可以考虑推出区间的强弱关系(比如 A 比 B 强,意味着 A 满足条件,则 B 一定满足条件),再让最强的一些区间满足条件,本质时贪心。
显然的贪心,设左指针 \(l\) 为 \(1\),拿一右指针 \(r\) 按序列从左往右扫,如果 \(a_l\sim a_r\) 是不合法的,将这区间里任意一个数改成一个从未出现过的数,再令 \(l=r+1\)。
现在的问题是如何判断一个区间是独特的,当 \(r\) 往右挪了之后,我们只需要判断以 \(r\) 为右端点的区间是否都是特殊的,用数据结构记录每个左端点是否合法。如果加进来了一个数 \(x\),设这个数前一次出现为 \(\text{las}_x\),前前次为 \(\text{llas}_x\),则令区间 \((\text{llas}_x,\text{las}_x]\) 减一,\((\text{las}_x,r]\) 加一。询问区间 \([l,r]\) 最小值,为 \(0\) 就不合法。其实就是动态让最后一次出现与倒数第二次之间的区间有标记。
CF1967B2 Reverse Card (Hard Version)
🔺key:若 \(\gcd(a,b)=1\),则 \(\gcd(a+b,b)=1\)。
设 \(a=pg,b=qg\),其中 \(p,q\) 互质。
\(qg^2=(pg+qg)k\)
\(qg=(p+q)k\)
而 \(\gcd(p,q)=1\),所以 \(\gcd(p+q,q)=1\),故 \(g\) 是 \(p+q\) 的倍数。
从而得出 \(p\le g\),故 \(p\le \frac{a}{p}\),\(p^2\le n\)。\(q\) 同理。直接枚举即可。
CF1957F2 Frequency Mismatch (Hard Version)
🔺key:询问有关一个区间某出现次数不同的颜色,可以考虑对颜色随机赋权后用主席树。
假设问题在序列上,询问两个区间出现次数不相同的颜色,可以把每个颜色随机赋一个值,随后用主席树,在两个区间上的颜色区域上二分哈希值,若左边儿子哈希值不同往左边递归,右儿子哈希值不同也往右递归,因为每次二分下去都必定能找到一个答案,所以询问一次复杂度是 \(O(k\log n)\) 的。
放到了树上就是在树上建立主席树。
CF1956F Nene and the Passing Game
🔺key:统计满足某个不等式的东西,可以移项后拆式子。
假设 \(i\ge j\)。
\(l_i+l_j\le i-j\le r_i+r_j\) 可以拆成两个式子:
故将二元组 \((i-l_i,0)\) 与 \((i+l_i,1)\) 混合排个序,维护一个数据结构,从左往右依次考虑(满足第一个不等式),若是二元组第二位为 \(0\),说明这是询问,把数据结构中 \(r_j+j\ge i-r_i\) 的 \(j\) 拿出来都与 \(i\) 连边。若是 \(1\),把 \(r_j+j\) 放进数据结构。
这样复杂度不对,注意到连边不用每次都连完,保留最大的 \(r_j+j\),剩下的满足 \(r_j+j\ge i-r_i\) 的 \(j\) 连玩之后就可以弹出了。用大根堆维护。
CF1955H The Most Reckless Defense
🔺key:当花费函数比收益函数增长地快得多,考虑自变量不会很大。
注意到 \(3^r\) 增长很快。实际上,当 \(r=12\) 时,就算是使用题目范围的最大火力也无法战胜。故题目简化成将塔与 \(r=1\sim 12\) 做匹配。
可以状压,设 \(f(i,S)\) 为前 \(i\) 个塔,被确认了半径的半径集合为 \(S\),最大伤害。枚举上一个被选的半径(或者不选)即可转移:
\(f(i,S)=\max\{f(i-1,S),f(i-1,S-\{j\})+p_i\times g(i,j)-3^j\}\)
\(g(i,j)\) 为第 \(i\) 个塔半径为 \(j\) 时能攻击敌人多少次。
因为是匹配问题,所以也可以费用流。
🔺key:算一个序列的答案,可以考虑已经算了某序列的答案,现在多加一个元素,对序列答案的增量是多少。同样的,这种方法可以应用到图(铺设道路)、置换(AGC045D)等。
当一个序列 \(\{a\}\) 的末尾增加一个数后,操作次数就要增加 \(\max(0,\lceil\frac{a_{n}}{k}\rceil-\lceil\frac{a_{n-1}}{k}\rceil)\),即:\(a_{n-1}\) 受到的操作,\(a_n\) 也会受到,且如果最后 \(a_n\) 还没被消完,还要单独搞。
故答案为 \(f(k)=\sum \max(0,\lceil\frac{a_{i}}{k}\rceil-\lceil\frac{a_{i-1}}{k}\rceil)\),整除分块即可。
CF1929F Sasha and the Wedding Binary Search Tree
🔺key:看到二叉树,想到拍扁。
看到二叉树就想到拍扁,现在的问题转换成一个序列上的组合问题了。
那么填充一个长度为 \(n\),开头 \(\ge L\),结尾 \(\le R\) 的不降序列方案数怎么计算?可以将第一个数加 \(0\),第二个数加 \(1\),……这样操作完后的序列就是结尾 \(\le R+n-1\) 的严格上升序列了,且与原序列形成双射。这样转换后方案数好算,为 \(C_{R-L+n}^n\)。
CF1957E Carousel of Combinations
🔺key:对组合数取模,可以考虑卢卡斯。对阶乘取模,可以考虑威尔逊。
把圆排列转换为熟悉的组合数,问题即:\(\sum_{i=1}^n\sum_{j=1}^i(C_i^{j}(j-1)! \bmod j)\)。
对于 \(C_i^j\),考虑卢卡斯定理,\(C_i^j\equiv C_{\lfloor i/j\rfloor}^{\lfloor j/j\rfloor}C_{i\bmod j}^{j\bmod j}\pmod j\)。
即:\(C_i^j\equiv \lfloor \frac{i}{j}\rfloor\pmod j\)。考虑原式组合数右边的 \((i-1)!\),考虑威尔逊定理:
-
当 \(j\) 为质数,有:\((j-1)!\equiv j-1\pmod j\)。
-
当 \(j\) 为 \(4\),有:\((j-1)!\equiv2\pmod j\)。
-
除此之外,都有:\((j-1)!\equiv0\pmod j\)。
也就是说 \(j\) 只有在质数以及 \(4\) 的情况下才对答案有贡献,枚举 \(j\) 后再枚举其倍数统计贡献即可。
🔺key:构造题,可以考虑其弱化版的多种方法,再将其应用到原题进行解法分治。
如果我们知道所有子区间的加和,那么如何做?
方法一:考虑子区间加和中出现出现奇数次的数字,其一定是跨序列中点且两边跨度相等的,即:
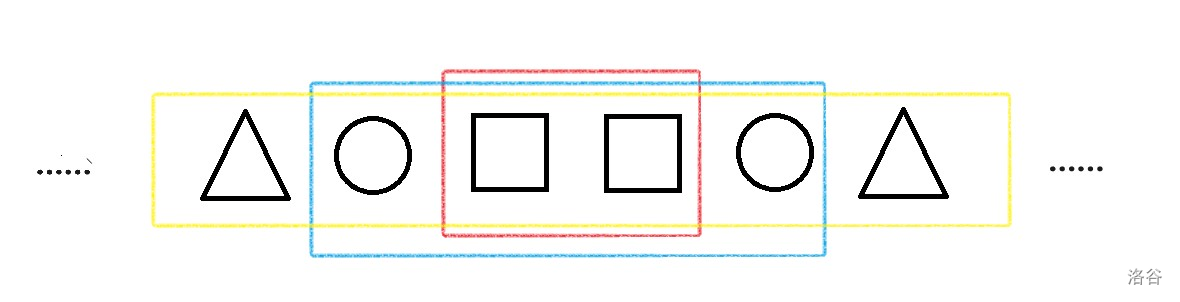
差分后即可算出每一个元素的值。
方法二:考虑子区间加和中的最大与次大,其一定是 \([1,n]\) 和 \([1,n-1]\),那我们可以得到 \(a_1\) 与 \(a_n\),从而得到 \([2,n-1]\) 和的值,删去后最大值一定是 \([1,n-2]\),再推出 \(a_2,a_{n-1}\),从而得到 \([3,n-2]\) 和的值,删去后最大值一定是 \([1,n-3]\),以此类推。
那么缺失一个元素后,如果最大值只出现一次,说明 \([1,n]\) 和是保留的,用方法二;若出现两次,说明 \([1,n]\) 被删了,用方法一算出 \(a_2\sim a_{n-1}\) 的信息后可以得到 \(a_1\)。
🔺key:一个序列的 \(k\) 阶前缀和,\(a_x\) 会对 \(a_y\) 贡献 \(C_{y-x+k-1}^{k-1}\) 倍代价,证法是 DP 后考虑组合意义。
对于一个点 \(u\),考虑其树状数组上的祖先 \(v\),\(u\) 与 \(v\) 的深度差为 \(d\),求 \(u\) 对 \(v\) 的贡献是多少,也就是 \(b_v\) 中 \(a_u\) 的系数为多少。
设 \(g(k,d)\) 为 \(k\) 轮操作后,深度差为 \(d\) 中的系数,则 \(g(k,d)=\sum_{i=1}^dg(k-1,i)\),考虑其组合意义,即走 \(k\) 次,每一次可以不走也可以走很多步,走完后恰好是 \(d\) 步的方案数,故 \(g(k,d)=C_{d+k-1}^{k-1}\)。依次枚举 \(u\) 及其祖先消除贡献即可。
🔺key:构造题可以猜测某些事情做的次数不会很多,甚至是常数级别的。
肯定让 Alice 第一次买一个价值 \(n-k+1\) 的物品,第二次买 \(k-1\) 个价值 \(1\) 物品。
\(n=k\) 时显然无解。\((k-1)\times 2<n\) 也无解,因为第一次的价格较低会让 Alice 买不止一个。
🔺key:双对称,即有周期性。
首先判断原串是否回文。
找到第一个与第一个字符不同的地方 \(pos\),则字符串形如 \(\texttt{aaaab}\cdots\),看是否能将字符串划分为 \([1,pos]\) 和 \([pos+1,n]\),两段都非回文,如果不行,再看是否能将字符串划分为 \([1,pos+1]\) 和 \([pos+2,n]\),再不行就无解。
为什么这样对?无解的情况形如 \(\texttt{abababa}\) (即:\(\texttt{ab+以a开头的回文串}\),且原串回文)或 \(\texttt{aaaabaaaa}\)(即:\(pos\) 恰好在中央),显然无解,否则两种方法必定有一个可行。
CF1916E Happy Life in University
枚举 LCA,用线段树维护颜色数最大值与次大值即可。
具体的,记 \(las_i\) 为节点 \(u\) 满足 \(u\) 与 \(i\) 同色,且 \(u\) 到 \(i\) 中没有这样的颜色的 \(u\) 的集合。把 LCA \(i\) 的颜色加入线段树时,\(dfn_i\sim edfn_i\) 都 \(+1\),但 \(las_i\) 集合中的子树是不用加这个颜色的,故 \(dfn_u\sim edfn_u(u\in las_i)\) 都再 \(-1\)。
🔺key:选出某些东西使得两两之间都满足限制,考虑最大团搜索。
将距离 \(\ge r\) 的点连边,题目就变成了最大团搜索了,使用 BK 算法。
🔺key:对于在平面上找到某个连续的满足某个性质的点(或线、面),可以发现其是某些离散的东西的交点等,从而转连续为离散。
可以把题意转换成寻找一个点 \(O\),使得做出图 \(G\) 关于 \(O\) 的对称图 \(G^\prime\),\(G\) 与 \(G^\prime\) 点构成的凸包面积最小(\(G\) 与 \(G^\prime\) 上的点都必须在凸包边缘上)。
容易发现,\(G\) 与 \(G^\prime\) 必有两处三点共线,其中一处的边是 \(G\) 的,另一处是 \(G^\prime\) 的,这两处都是对应的。
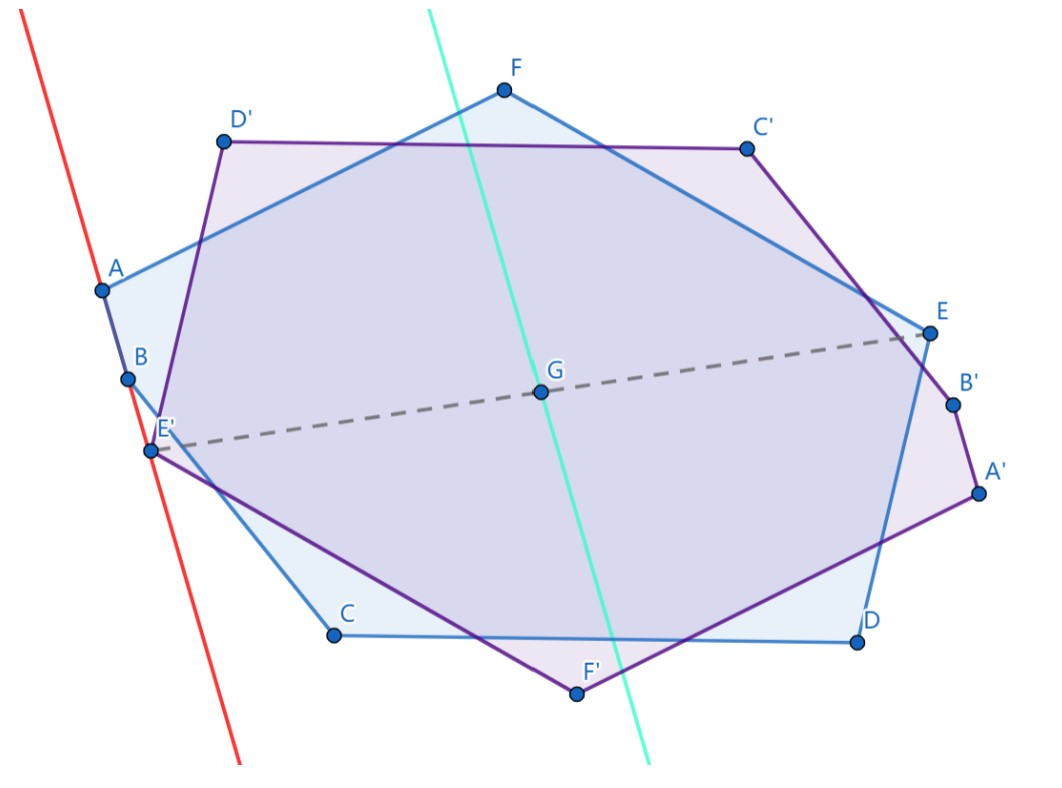
别人的图,侵删。比如上图就是 \(AB\) 与 \(E^\prime\) 共线;\(A^\prime B^\prime\) 与 \(E\) 共线。
为了满足上述要求,可能的 \(O\) 点就在 \(G\) 的一条边 \((a,b)\) 与 \(G\) 上另外的一个点 \(c\) 构成的三角形中 \((a,b)\) 对应的中位线上。
于是两两枚举中位线,求其交点就是可能的答案,每次以它为 \(O\) 算一遍凸包,复杂度 \(O(n^5\log n)\)。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号