前缀和与差分

参考：

(40条消息) 前缀和与差分 图文并茂 超详细整理（全网最通俗易懂）_林小小小鹿的博客-CSDN博客_前缀和与差分

一维前缀和：

输入一个长度为n的整数序列。接下来再输入m个询问，每个询问输入一对l, r。对于每个询问，输出原序列中从第l个数到第r个数的和。

思路：

1.需要一个数组s[N]来分别求前i项和：
s[i]=a[1]+a[2]+...+a[i];

(s[i]=s[i-1]+a[i]:根据s[i-1]求s[i])

2.求l到r项和时，根据询问直接调用便可：

s[r]-s[l-1];

时间复杂度仅为o(m+n)

 

例题：

输入一个长度为n的整数序列。

接下来再输入m个询问，每个询问输入一对l, r。

对于每个询问，输出原序列中从第l个数到第r个数的和。

输入格式

第一行包含两个整数n和m。

第二行包含n个整数，表示整数数列。

接下来m行，每行包含两个整数l和r，表示一个询问的区间范围。

输出格式

共m行，每行输出一个询问的结果。

数据范围

1≤l≤r≤n,

1≤n,m≤100000,

−1000≤数列中元素的值≤1000

输入样例：

5 3

2 1 3 6 4

1 2

1 3

2 4

输出样例：

3

6

10

#include<bits/stdc++.h>
using namespace std;
int m,n,l,r;
const int N=1000;
int a[N];
int s[N];
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
    }
    memset(s,0,sizeof(s));
    for(int i=1;i<=n;i++)
    {
        //计算前缀和数组 
        s[i]=s[i-1]+a[i];
    }
    while(m--)
    {
        //输出l到r的和=(a[1]+a[2]+...+a[r])-(a[1]+a[2]+...a[l-1])=a[l]+...+a[r];
        cin>>l>>r;
        cout<<s[r]-s[l-1]<<endl;
    }
    return 0;
}

 

 

二维前缀和：

步骤：

1.计算前缀和数组s

2.计算s[x1][y1]-s[x2][y2]

 

 

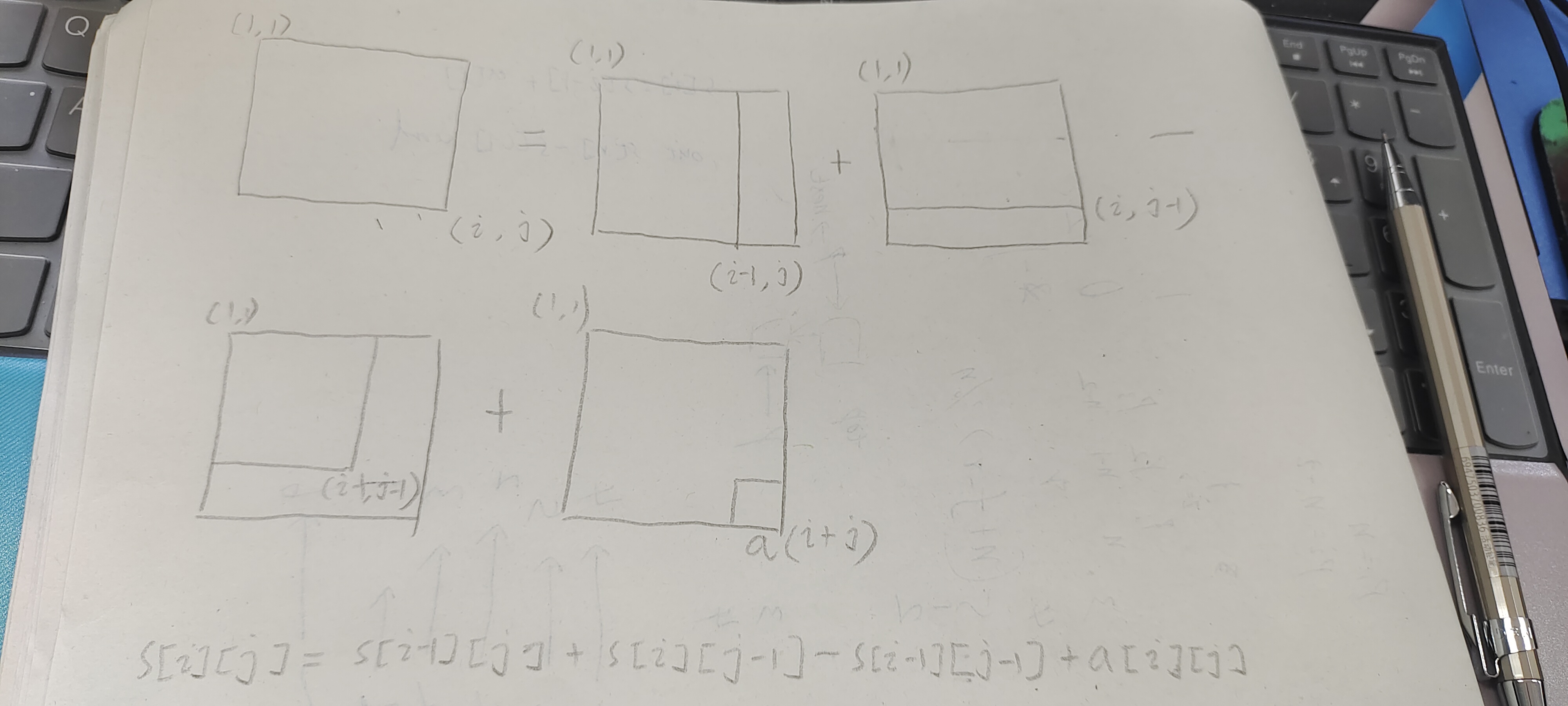
 输入一个n行m列的整数矩阵，再输入q个询问，每个询问包含四个整数x1, y1, x2, y2，表示一个子矩阵的左上角坐标和右下角坐标。对于每个询问输出子矩阵中所有数的和。

例：

输入一个n行m列的整数矩阵，再输入q个询问，每个询问包含四个整数x1, y1, x2, y2，表示一个子矩阵的左上角坐标和右下角坐标。

 

对于每个询问输出子矩阵中所有数的和。

 

输入格式

第一行包含三个整数n，m，q。

 

接下来n行，每行包含m个整数，表示整数矩阵。

 

接下来q行，每行包含四个整数x1, y1, x2, y2，表示一组询问。

 

输出格式

共q行，每行输出一个询问的结果。

 

数据范围

1≤n,m≤1000,

1≤q≤200000,

1≤x1≤x2≤n,

1≤y1≤y2≤m,

−1000≤矩阵内元素的值≤1000

输入样例：

3 4 3

1 7 2 4

3 6 2 8

2 1 2 3

1 1 2 2

2 1 3 4

1 3 3 4

输出样例：

17

27

21

 

#include<bits/stdc++.h>
using namespace std;
int n,m,q;
const int N=2000;
int a[N][N];
int s[N][N];
int x1,y,x2,y2;// y1 和 C++ 标准库中的某个变量名称冲突，这个问题应当引起注意
int main()
{
    cin>>n>>m>>q;
    memset(s,0,sizeof(s));
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            cin>>a[i][j];
        }
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            //求出每前s[i][j]项的和 
            s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];
        }
    }
    while(q--)
    {
        cin>>x1>>y>>x2>>y2;
        //求出s[x1][y1]-s[x2][y2] 
        int sum=s[x2][y2]-s[x1-1][y2]-s[x2][y-1]+s[x1-1][y-1];
        cout<<sum<<endl;
    }
    return 0;
 } 

 

 

 

差分：后一项减前一项的差(a[i]-a[i-1])

一维分差：

思路：

1.原数组为a，分差数组为b（原数组为差分数组的前缀和数组）

2.b[i]=a[i]-a[i-1];

3.求[l,r]区间内所有数加上c后的序列

4.只需要把b[l]+c，然后再将b[r+1]-c进行还原便可

5.最后输出 b[i]+=b[i-1];

例如：

A：1 2 3 4 5 6

B：1 1 1 1 1 1

此时要把[2,4]区间加上3

则：b[2]+3;

此时：1 4 1 1 1 1

如果直接输出则为：

1 5 6 7 8 9

此时的含义是把[2,6]加了3

我们只要[2,4]加3，所以要从b[5]开始减3

即：B：1 4 1 1 -2 1

输出：1 5 6 7 5 6

 

例：

输入一个长度为n的整数序列。

接下来输入m个操作，每个操作包含三个整数l, r, c，表示将序列中[l, r]之间的每个数加上c。

请你输出进行完所有操作后的序列。

输入格式

第一行包含两个整数n和m。

第二行包含n个整数，表示整数序列。

接下来m行，每行包含三个整数l，r，c，表示一个操作。

输出格式

共一行，包含n个整数，表示最终序列。

数据范围

1≤n,m≤100000,

1≤l≤r≤n,

−1000≤c≤1000,

−1000≤整数序列中元素的值≤1000

输入样例：

6 3

1 2 2 1 2 1

1 3 1

3 5 1

1 6 1

输出样例：

3 4 5 3 4 2

#include<bits/stdc++.h>
using namespace std;
int l,r,c,n,m;
const int N=1000;
int a[N],b[N];//a[0]=0 
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
    }
    //构造差分数组b 
    for(int i=1;i<=n;i++)
    { 
        b[i]=a[i]-a[i-1];
    }
    //[l,r]+c l的差分数组变化时，a[l]到a[n]的值都会变化，因此需要在r-1处还原 
    while(m--)
    {
        cin>>l>>r>>c;
        //b[l]+c 
        b[l]+=c;
        //还原 
        b[r+1]-=c;
    }
    //遍历 
    for(int i=1;i<=n;i++)
    {
        b[i]+=b[i-1];//核心：用差分数组求变化后的数组 
        cout<<b[i]<<" ";
    }
    return 0;
}

 

 

 

二维差分

1.构建差分数组

2.计算a[x1][y1]~a[x2][y2]+c

3.遍历

 

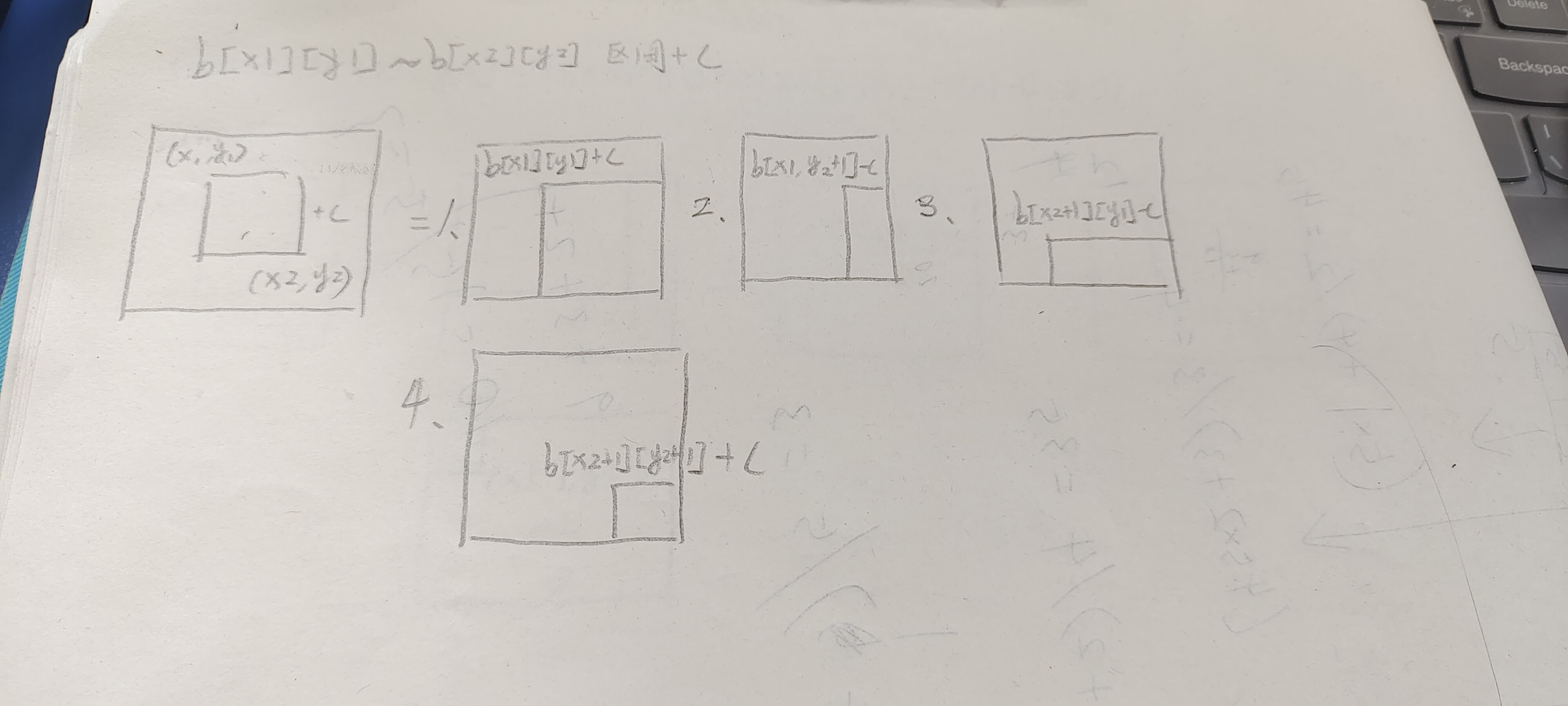
输入一个n行m列的整数矩阵，再输入q个操作，每个操作包含五个整数x1, y1, x2, y2, c，其中(x1, y1)和(x2, y2)表示一个子矩阵的左上角坐标和右下角坐标。

每个操作都要将选中的子矩阵中的每个元素的值加上c。

请你将进行完所有操作后的矩阵输出。

输入格式

第一行包含整数n,m,q。

接下来n行，每行包含m个整数，表示整数矩阵。

接下来q行，每行包含5个整数x1, y1, x2, y2, c，表示一个操作。

输出格式

共 n 行，每行 m 个整数，表示所有操作进行完毕后的最终矩阵。

数据范围

1≤n,m≤1000,

1≤q≤100000,

1≤x1≤x2≤n,

1≤y1≤y2≤m,

−1000≤c≤1000,

−1000≤矩阵内元素的值≤1000

输入样例：

3 4 3

1 2 2 1

3 2 2 1

1 1 1 1

1 1 2 2 1

1 3 2 3 2

3 1 3 4 1

输出样例：

2 3 4 1

4 3 4 1

2 2 2 2

//a是b的前缀和数组，改变b[i][j]会影响a[i][j]以及以后的每一个值 
#include<bits/stdc++.h>
using namespace std;
const int N=1000;
int a[N][N];
int b[N][N];
int x1,y,x2,y2,c;
int insert(int x1,int y,int x2,int y2,int c)
{
    b[x1][y]+=c;
    b[x1][y2+1]-=c;
    b[x2+1][y]-=c;
    b[x2+1][y2+1]+=c;
}
int main()
{
    int m,n,q;
    cin>>n>>m>>q; 
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            cin>>a[i][j];
            //构建差分数组，b[i][j]~b[i][j]，每一个点为一个单位 
            //使得a数组中a[i][j]是b数组左上角(1,1)到右下角(i,j)所包围矩形元素的和。
            //a数组是b数组的前缀和数组，b数组只对a数组负责 
            insert(i,j,i,j,a[i][j]);
        }
    }
    //更新差分数组 
    while(q--)
    {
        cin>>x1>>y>>x2>>y2>>c;
        insert(x1,y,x2,y2,c); 
    }
    //求出每一项，即求b[i][j]的前缀和 ，只是a[i][j]=b[i][j] 
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            b[i][j]+=b[i-1][j]+b[i][j-1]-b[i-1][j-1];
        }
    }
    //遍历 
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
            cout<<b[i][j]<<" ";
         cout<<endl;
    }
    return 0;
}