树链剖分

问题

对于树上路径上的信息进行修改和查询操作

算法思想

对于树上的每个节点，将其节点最多的子树对应的儿子称为重儿子，其他儿子称为轻儿子，连接重儿子和其父亲的边称为重边，其余边称为轻边。那么这棵树会被划分为一条条由重边和其连接的节点组成的链，称为重链。每条链由轻儿子开头，一直延申至叶节点。如图所示。

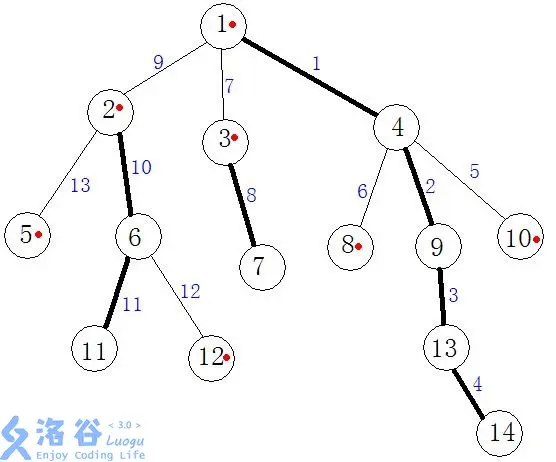
由于从下往上，每经过一条轻边，子树大小至少扩大两倍，所以从叶节点到根节点最多经过 \(log_2n\) 条轻边（即重链）。所以进行路径操作时可以将每条重链进行整体操作，对轻边进行单独操作，这样每次操作的复杂度为 \(O(log_2n\times维护重链所用数据结构复杂度)\) 。

代码实现

P3384 【模板】重链剖分/树链剖分

#include <bits/stdc++.h>

#define int long long

using namespace std;

int read() {
    int x = 0, f = 1; char ch = getchar();
    while (ch < '0' || ch > '9') {if (ch == '-') f = -1; ch = getchar();}
    while (ch >= '0' && ch <= '9') {x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
    return x * f;
}

const int N = 1e5 + 10;

int n, m, r, p;
int head[N];
int a[N];
int fa[N], dep[N], siz[N], son[N], in[N], out[N], nfd[N], top[N];
int tot, cnt;

struct node {
    int nxt, to;
} e[N << 1];

struct SEGT {
    #define ls (k << 1)
    #define rs (k << 1 | 1)
    #define mid ((l + r) >> 1)

    int sum[N << 2], tag[N << 2];

    void pushdown(int k, int l, int r) {
        sum[ls] += (mid - l + 1) * tag[k] % p; sum[ls] %= p;
        sum[rs] += (r - mid) * tag[k] % p; sum[rs] %= p;
        tag[ls] += tag[k]; tag[ls] %= p;
        tag[rs] += tag[k]; tag[rs] %= p;
        tag[k] = 0;
    }

    void build(int k, int l, int r) {
        if (l == r) {
            sum[k] = a[nfd[l]];
            return;
        }
        build(ls, l, mid);
        build(rs, mid + 1, r);
        sum[k] = (sum[ls] + sum[rs]) % p;
    }

    void modify(int k, int l, int r, int L, int R, int d) {
        if (l >= L && r <= R) {
            sum[k] += (r - l + 1) * d; sum[k] %= p;
            tag[k] += d; tag[k] %= p;
            return;
        }
        pushdown(k, l, r);
        if (L <= mid) modify(ls, l, mid, L, R, d);
        if (R > mid) modify(rs, mid + 1, r, L, R, d);
        sum[k] = (sum[ls] + sum[rs]) % p;
    }

    int query(int k, int l, int r, int L, int R) {
        if (l >= L && r <= R) return sum[k];
        pushdown(k, l, r);
        int tmp = 0;
        if (L <= mid) tmp = (tmp + query(ls, l, mid, L, R)) % p;
        if (R > mid) tmp = (tmp + query(rs, mid + 1, r, L, R)) % p;
        sum[k] = (sum[ls] + sum[rs]) % p;
        return tmp;
    }
} t;

void adde(int x, int y) {
    e[++tot].to = y;
    e[tot].nxt = head[x];
    head[x] = tot;
}

void dfs1(int u, int f, int d) {
    fa[u] = f;
    dep[u] = d;
    siz[u] = 1;
    for (int i = head[u]; i; i = e[i].nxt) {
        int v = e[i].to;
        if (v == f) continue;
        dfs1(v, u, d + 1);
        siz[u] += siz[v];
        if (siz[v] > siz[son[u]]) son[u] = v;
    }
}

void dfs2(int u, int f, int tp) {
    in[u] = ++cnt;
    nfd[cnt] = u;
    top[u] = tp;
    if (son[u]) dfs2(son[u], u, tp);
    for (int i = head[u]; i; i = e[i].nxt) {
        int v = e[i].to;
        if (v == f || v == son[u]) continue;
        dfs2(v, u, v);
    }
    out[u] = cnt;
}

void modify1(int x, int y, int d) {
    while (top[x] != top[y]) {
        if (dep[top[x]] < dep[top[y]]) swap(x, y);
        t.modify(1, 1, n, in[top[x]], in[x], d);
        x = fa[top[x]];
    }
    if (dep[x] > dep[y]) swap(x, y);
    t.modify(1, 1, n, in[x], in[y], d);
}

void modify2(int x, int d) {
    t.modify(1, 1, n, in[x], out[x], d);
}

int query1(int x, int y) {
    int tmp = 0;
    while (top[x] != top[y]) {
        if (dep[top[x]] < dep[top[y]]) swap(x, y);
        tmp += t.query(1, 1, n, in[top[x]], in[x]);
        tmp %= p;
        x = fa[top[x]];
    }
    if (dep[x] > dep[y]) swap(x, y);
    tmp += t.query(1, 1, n, in[x], in[y]);
    tmp %= p;
    return tmp;
}

int query2(int x) {
    return t.query(1, 1, n, in[x], out[x]);
}

signed main() {
    n = read(); m = read(); r = read(); p = read();
    for (int i = 1; i <= n; i++) a[i] = read() % p;
    for (int i = 1; i <= n - 1; i++) {
        int x = read(), y = read();
        adde(x, y); adde(y, x);
    }
    dfs1(r, 0, 1);
    dfs2(r, 0, r);
    t.build(1, 1, n);
    for (int i = 1; i <= m; i++) {
        int q = read();
        if (q == 1) {
            int x = read(), y = read(), d = read();
            modify1(x, y, d);
        }
        if (q == 2) {
            int x = read(), y = read();
            printf("%lld\n", query1(x, y));
        }
        if (q == 3) {
            int x = read(), z = read();
            modify2(x, z);
        }
        if (q == 4) {
            int x = read();
            printf("%lld\n", query2(x));
        }
    }
    return 0;
}