最大流算法（Dinic算法）

问题

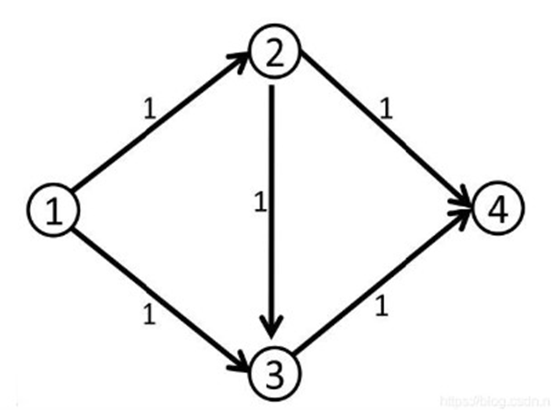
给出一个网络图，以及其源点和汇点，求出其网络最大流

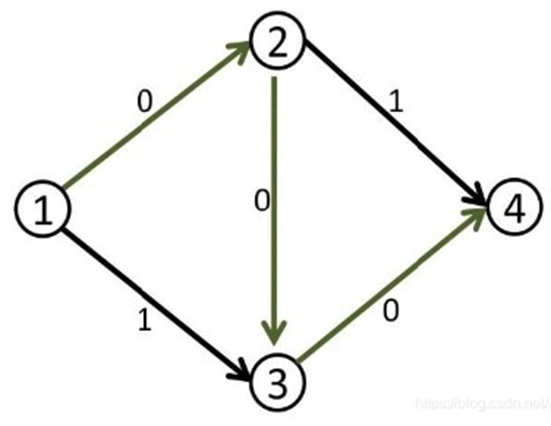
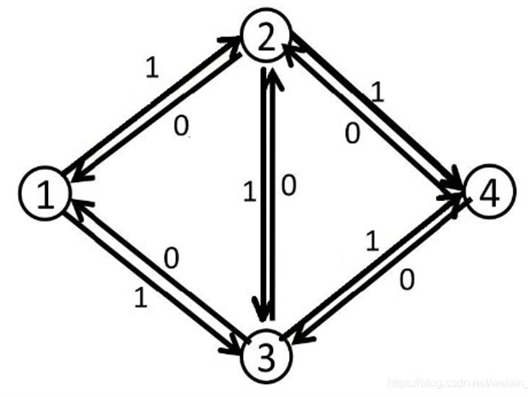
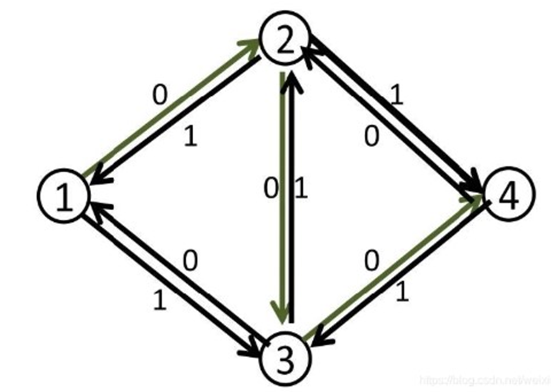
Dinic算法

算法的主要思想是构造反向边，通过不断寻找增广路来求出最大流，辅以一些优化来减小复杂度

代码实现

P3376 【模板】网络最大流

#include <bits/stdc++.h>

#define ll long long

using namespace std;

int read() {
    int x = 0, f = 1; char ch = getchar();
    while (ch < '0' || ch > '9') {if (ch == '-') f = -1; ch = getchar();}
    while (ch >= '0' && ch <= '9') {x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
    return x * f;
}

const int N = 5e4 + 10;
const ll inf = 1e18;

int n, m, s, t;
int head[N];
int vis[N], now[N];
ll dis[N];
int tot = 1;

struct node {
    int to, nxt;
    ll w;
} e[N << 1];

void adde(int x, int y, ll w) {
    e[++tot].to = y;
    e[tot].nxt = head[x];
    e[tot].w = w;
    head[x] = tot;
}

int bfs() {
    for (int i = 1; i <= n; i++) dis[i] = inf;
    queue<int> q;
    q.push(s);
    dis[s] = 0;
    now[s] = head[s];
    while (!q.empty()) {
        int u = q.front();
        q.pop();
        for (int i = head[u]; i; i = e[i].nxt) {
            int v = e[i].to;
            if (e[i].w > 0 && dis[v] == inf) {
                q.push(v);
                now[v] = head[v];
                dis[v] = dis[u] + 1;
                if (v == t) return 1;
            }
        }
    }
    return 0;
}

ll dfs(int u, ll sum) {
	if (u == t) return sum;
	ll tmp,res = 0;
	for (int i = now[u]; i && sum; i = e[i].nxt) {
		now[u] = i;
		int v = e[i].to;
		if (e[i].w > 0 && dis[v] == dis[u] + 1) {
			tmp = dfs(v,min(sum,e[i].w));
			if (tmp == 0) dis[v] = inf;
			e[i].w -= tmp;
			e[i ^ 1].w += tmp;
			res += tmp;
			sum -= tmp;
		}
	}
	return res;
}

ll dinic() {
    ll res = 0, tmp = 0;
    while (bfs()) {
        while (tmp = dfs(s, inf)) res += tmp;
    }
    return res;
}

int main() {
    n = read(); m = read(); s = read(); t = read();
    for (int i = 1; i <= m; i++) {
        int x = read(), y = read(), z = read();
        adde(x, y, z);
        adde(y, x, 0);
    }
    printf("%lld", dinic());
    return 0;
}