莫比乌斯反演

莫比乌斯函数

当 \(\exists p>1,p^2|n\) 时，\(\mu(n)=0\)，否则设 \(n\) 的本质不同质因数个数为 \(k\)，\(\mu(n)=(-1)^k\)。

μ(n) 的线性筛递推求法

//μ(n)和d(n)（约数个数函数）的线性推法
for(int i=2;i<=5e4;i++){
	if(!v[i])mu[i]=-1,d[i]=2,p[++n_p]=i;
	for(int j=1;j<=n_p&&p[j]*i<=5e4;j++){
		v[i*p[j]]=1;
		if(i%p[j])mu[i*p[j]]=-mu[i],d[i*p[j]]=2*d[i];
		else {mu[i*p[j]]=0,d[i*p[j]]=2*d[i]-d[i/p[j]];break;}
	}
}

几个重要函数及其性质

\(\varepsilon(n)=[n=1]\)
\(\varphi(n)\)
\(id(n)=n\)
\(\mu(n)\)

---

性质一. \(\varepsilon(n)=\sum_{d|n}\mu(d)\)
性质二. \(id(n)=\sum_{d|n}\varphi(d)\)

反演

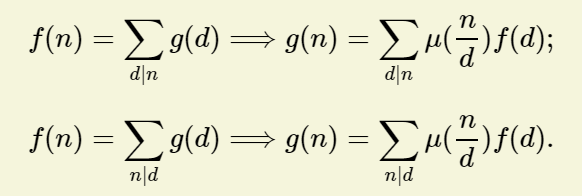
前置知识

一、整除分块
你需要知道这样一种整除分块，它要对 \((\lfloor\frac ni\rfloor,\lfloor\frac mi\rfloor)\) 这个二元组进行 \(i\) 的分块，也就是同一个块内不仅要满足 n/i 相同，还要满足 m/i 相同。显然我们把每次的右块端点从 \(j=n/(n/i)\) 改成 \(j=\min(n/(n/i),m/(m/i))\) 即可，复杂度不变。

二、欧拉筛
用欧拉筛递推与 \(f(n)=\sum_{d|n}\text{something}\) 有关的一些信息。

化简套路

一、利用性质（等量关系）化简
看到 \([...=1]\) 的条件反射，以及对于一个数的主动分解成 \(\sum\phi(d)\)，又及主动分解 \(\varphi(n)=\sum_{i=1}^n[\gcd(i,n)=1]\)。

二、一些常见结构的处理方式
\(\sum_{i=1}^n\sum_{j=1}^m\sum_{d|\gcd(i,j)}\)：\(\sum_{d=1}^{\min(n,m)}\sum_{d|i,i\le n}\sum{d|j,j\le m}\)
\(\sum_{a=1}^n\sum_{b=1}^m\operatorname{lcm}(a,b)\)：\(\sum_a\sum_b\frac{ab}{\gcd(a,b)}=\sum_{d=1}^{\min(n,m)}d\sum_{i=1}^{\lfloor \frac nd\rfloor}\sum_{j=1}^{\lfloor\frac md\rfloor}[\gcd(i,j)=1]ij\)
\(\sum_{i=1}^n\sum_{j=1}^m ij\)：\(sum(n)sum(m)\)

习题

[POI2007]Zap
[spoj]LCMSum
[国家集训队]jzptab
[NOI2010]能量采集
YY的GCD
[bzoj]Lcm
[SDOI2015]约数个数和