平面几何基础知识简笔
向量内外积
- 内积(点积,\(\bm{a\cdot b}\)):
- \(=x_1x_2+y_1y_2\)
- \(=|a||b|\cos\lang a,b\rang\)
- 是标量
- 外积(叉积,\(\bm{a\times b}\)):
- \(=x_1y_2-x_2y_1\)
- 模长 \(=|a||b|\sin\lang a,b\rang\)
- 【几何意义】数值上 = 以 \(\bm{a,b}\) 为邻边的平行四边形的面积。
- 是向量
正余弦定理
- 正弦定理:在 \(\triangle ABC\) 中,\(R\) 为外接圆半径,
\[{a\over\sin A}={b\over\sin B}={c\over\sin C}=2R
\]
- 余弦定理:在 \(\triangle ABC\) 中,
\[a^2=b^2+c^2-2bc\cos A\\
b^2=a^2+c^2-2ac\cos B\\
c^2=a^2+b^2-2ab\cos C\\
\]
顺逆时针
用 \(\bm{a\times b}\) 的符号判断 \(\bm{b}\) 相对于 \(\bm{a}\) 在的方向:“顺负逆正”。
极角排序
bool operator<(P a,P b){return atan2(a.y,a.x)<atan2(b.y,b.x);}
//atan2是求从原点出发的向量的逆时针旋转角
多边形面积
求多边形 \(P_1P_2...P_n\) 的面积。(多边形可凹可凸)
以平面任一点为原点 \(O\) 对 \(P_i\) 逆时针极角排序。
则多边形面积 \(S=\frac12(\bm{OP_1\times OP_2+OP_2\times OP_3+...+OP_{n-1}\times OP_n+OP_n\times OP_1}).\)
距离
- 欧几里得距离 \(\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\);
曼哈顿距离 \(|x_1-x_2|+|y_1-y_2|\);
切比雪夫距离 \(\max(|x_1-x_2|,|y_1-y_2|)\); - 曼哈顿转切比雪夫 \((x,y)\to(x+y,x-y)\);
切比雪夫转曼哈顿 \((x,y)\to(\frac{x+y}2,\frac{x-y}2)\).
圆与直线的公式
- 圆与直线的交点:
- 判断直线与圆的位置关系
- 求圆心在直线上的投影点
- 求直线的单位向量 \(\bm u\)
- 求弦长的一半,乘以 \(±\bm u\) 再加上投影点即答案
- 圆与圆的交点:
- 判断圆与圆的位置关系
- 求圆心间的距离 \(R\)
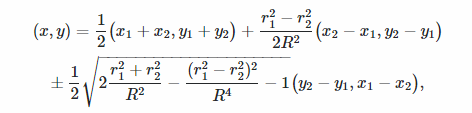


 浙公网安备 33010602011771号
浙公网安备 33010602011771号