[JOISC2014] 两个人的星座 解题报告

平面上的 \(n\) 个三三不共线点带颜色 \(0/1/2\)，合格三角形需满足三个顶点颜色互不相同，一个星座定义为由恰好两个互不交不含的合格三角形组成的图形，求星座的方案数。

Intuition

观察一个任意星座

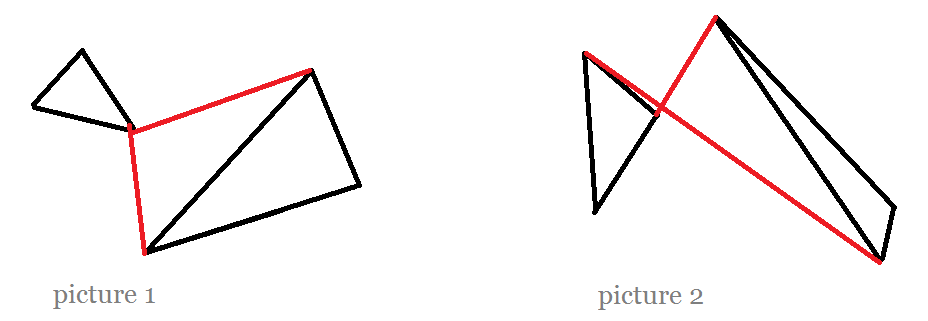
两个图案的共同之处在于，存在恰好两条分别连接两方三角形顶点的线段，使两三角形各自位于线段两侧。称，这样的线段为三角形的内公切线（外公切线：~同侧）。

考虑两三角形内公切线不同的星座，一定是不同的星座。据此，产生枚举内公切线并计算组合方案的思路。

Solution

枚举内公切线

当然可以 \(n^2\) 枚举两个端点，但这样无序的枚举时间复杂度显然太大。
考虑枚举一个端点，定住它并顺时针枚举另一个端点，将所有点分成两个半平面，每个半平面的点根据颜色来计算组合方案。

计算组合方案

考虑：确定内公切线段后，确定星座的剩余四个顶点的方案数。
首先会想到公切线两侧各有 2 个点，每边的都可以或者跟公切线的一个端点连或者跟公切线的另一个端点连。但是其实是没有必要的，因为

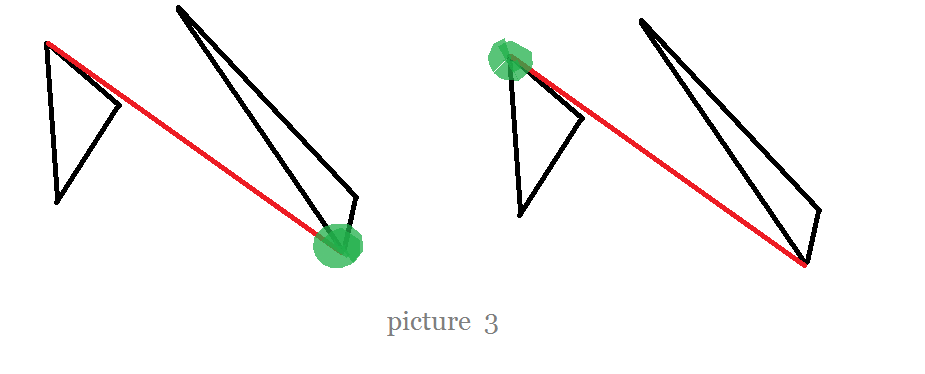
（标绿色的点为被定住的点）会统计同一对三角形。
因此，只需要规定一下定住的点必须选公切线顺时针还是逆时针方向的半平面。【这里是有讲究的，后面说】

接下来就是计算组合方案，直接用一个 int cnt[3] 记录某个半平面颜色数（并维护之）+乘法原理即可。

#include <bits/stdc++.h>
using namespace std;
const int N=3005;
typedef long long ll;
int n,all[3],cnt[3];
ll ans;
struct star {
	int x,y,c;
	double TAN; //预处理出atan2(y,x)的值可以在极角排序中减少常数
	ll operator*(const star &o)const{return 1ll*x*o.y-1ll*y*o.x;}//向量叉积
	bool operator<(const star &o)const{return TAN<o.TAN;}//极角排序比较函数
}a[N],o;
vector<star>t;
signed main(){
	cin>>n;
	for(int i=1;i<=n;i++)cin>>a[i].x>>a[i].y>>a[i].c,all[a[i].c]++;
	for(int i=1;i<=n;i++){
		o=a[i];//定住它……
		t.clear();
		for(int j=1;j<=n;j++)if(j!=i)t.push_back((star){a[j].x-a[i].x,a[j].y-a[i].y,a[j].c,atan2(a[j].y-a[i].y,a[j].x-a[i].x)});
		sort(t.begin(),t.end());//极角排序
		memset(cnt,0,sizeof(cnt));//注意清空
		for(int l=0,r=0;l<n-1;l++){
			while(r<l+n-1&&t[l]*t[r%(n-1)]>=0){//向量积：AxB确定B相对A位置——顺负逆正零共线
				cnt[t[r%(n-1)].c]++;
				r++;
			}
			int u1=(o.c+1)%3,v1=(u1+1)%3,u2=(t[l].c+1)%3,v2=(u2+1)%3;//异色
			ans+=1ll*cnt[u2]*cnt[v2]*(all[u1]-cnt[u1])*(all[v1]-cnt[v1]);//【讲究】见后
			cnt[t[l].c]--;
		}
	}
	cout<<ans/2;//一个星座两条内公切线，因此还会重复统计
}

【讲究】

具体见 https://www.luogu.com.cn/discuss/401896 。

---

Intuition 之类的东西以后都写进题解。