换根 DP 学习笔记 & 题解【[APIO2014]连珠线】

概述

本题为换根 DP 经典题，比较模板，借此题整理换根 DP。

题意简述

今构造一棵由珠子和线构成的树，可以通过下列方式中的一种添加一个新珠子：

1. 将一颗新珠子和已有的一颗珠子用红线连接起来；
2. 将一颗新珠子插入到两颗用红线连接的已有珠子之间。具体地，拆除原来的红线，并用蓝线将新珠子分别与两颗珠子相连。

每条线有一个权值。现在已经知道树的结构和每条线的权值，但不知道每条线的颜色。你需要输出合法的构造方式中，蓝线权值和的最大值。

提示

对于拿到的这棵树，随便选择一个点作为根，那么容易发现蓝线的产生只可能是下面两种方式（形态）：

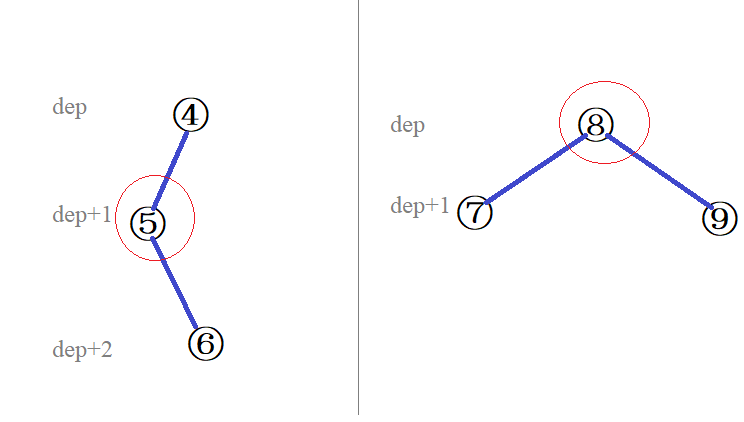
（打红圈的是某一时刻插入的新珠子）

假如我们分类讨论地 DP 子树中的这两种形态的蓝线权值和最大值，会发现这是十分困难的。

同时，我们意识到这样子分成两种形态是十分生硬的，因为它们本质是一样的。

考虑这两种形态能否一统为一：你会发现必然存在一个节点，使得以它为根时所有的蓝线都是可以以上左图的方式构造的。

例如，样例图中，以 10 为根就可以实现：

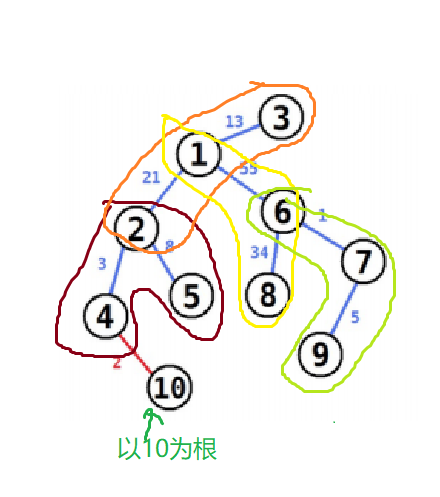
题解

根据提示，我们可以进行换根 DP。即：

• 先进行第一轮 dfs，求出以 1 为根的时候的按上左图方式构造最大的蓝线长度和 \(f_{i,0/1}\)。

  • \(f_{i,0/1}\) 表示以 \(i\) 为根的子树内，\(i\) 是不是（\(1/0\)）“重要点”（即上上图中的打红圈的点）的答案（例如上图中 \(f_{2,1}=3+2+21+8=34\)）。
  • \(f_{i,0}=\sum_{j\in son(i)}\max(f_{j,0},f_{j,1}).\)
  • 由于上述转移方式不利于后期代码实现，因此更改 \(f_{i,1}\) 的定义：
    • 上图中 \(f_{2,1}\) 只算 \(f_{2,1}=3+2+8=13\)（\(21\) 先不算，等 1 号点算的时候再加上）
    • 也就是说，只记录原 \(f_{i,1}\) 算的边当中真的在 \(i\) 的子树中的部分。
  • 于是 \(f_{i,0}=\sum_{j\in son(i)}\max(f_{j,0},f_{j,1}+w(i,j)).\)
  • 写 \(v=\min_{j\in son(i)}\{\max(f_{j,0},f_{j,1}+w(i,j))-(f_{j,0}+w(i,j))\}\)，则 \(f_{i,1}=f_{i,0}-v\)

• 在进行第二轮 dfs（换根），求出以不同节点为根时的答案。

  • \(g_{i,0/1}\) 记录 \(i\) 被某一个儿子吊起时，\(i\) 子树内的 \(f_{0/1}\)。注：\(g_{i,0/1}\) 会根据是被哪一个儿子吊起重新计算，因此复杂度不正确，后面会优化。

  • 记 \(F_{0}=f,F_1=g\)。

  • 则有

    \[F_{1,i,0}=\sum_{j\in link(i),j\ne p}\max(F_{j=fa[i],j,0},F_{j=fa[i],j,1}+w(i,j))\\ v=\min_{j\in link(i),j\ne p}\{\max(F_{j=fa[i],j,0},F_{j=fa[i],j,1}+w(i,j)-(F_{j=fa[x],j,0}+w(i,j))\}\\ F_{1,i,1}=F_{1,i,0}-v \]

    其中 \(p\) 表示吊起 \(i\) 的儿子，\(link(i)\) 表示与 \(i\) 相连的所有点的集合，\(fa[i]\) 代表以 1 为根时 \(i\) 的父节点，\(j=fa[i]\) 为一个 \(0/1\) 值。

• 时间复杂度在菊花树时可能被卡到 \(O(n^2)\)，无法通过。

• 发现每次查询的本质其实是 \(link(i)\) 除去一个元素后的 \(\max(F_{j=fa[i],j,0},F_{j=fa[i],j,1}+w(i,j))\) 之和，以及 \(\max(F_{j=fa[i],j,0},F_{j=fa[i],j,1}+w(i,j)-(F_{j=fa[x],j,0}+w(i,j))\) 的最小值。这种东西容易通过预处理出所求表达式的前缀值和后缀值，然后算 \(val_{pre}[i-1]\otimes val_{suf}[i+1]\) 来获得，其中 \(\otimes\) 表示一种合并运算，对应上面的 \(+\) 或 \(\min\)。

• 这样一来，复杂度被降到了 \(O(n)\)。

代码

#include <bits/stdc++.h>
using namespace std;
const int N=2e5+5;
int n,ans,f[2][N][2],fa[N];
vector<pair<int,int> >G[N],vec[N],val[2][N];
void dfs1(int x,int p,int pe){
	fa[x]=p;
	int v=1e9;
	for(int i=0;i<G[x].size();i++){
		int y=G[x][i].first,z=G[x][i].second;
		if(y^p){
			dfs1(y,x,z);
			f[0][x][0]+=max(f[0][y][0],f[0][y][1]+z);
			v=min(v,max(f[0][y][0],f[0][y][1]+z)-(f[0][y][0]+z));
		}
	}
	f[0][x][1]=f[0][x][0]-v;
}
void calc(int x){
	int v=1e9,tot=0;
	vec[x].resize(G[x].size()+2),val[0][x].resize(G[x].size()+2),val[1][x].resize(G[x].size()+2);
	for(int i=0;i<G[x].size();i++){
		int y=G[x][i].first,z=G[x][i].second;
		vec[x][++tot]=G[x][i];
		f[1][x][0]+=max(f[y==fa[x]][y][0],f[y==fa[x]][y][1]+z);
		v=min(v,max(f[y==fa[x]][y][0],f[y==fa[x]][y][1]+z)-(f[y==fa[x]][y][0]+z));
	}
	val[0][x][0]=val[1][x][tot+1]=make_pair(0,1e9);
	for(int i=1;i<=tot;i++){
		int y=vec[x][i].first,z=vec[x][i].second;
		val[0][x][i]=make_pair(val[0][x][i-1].first+max(f[y==fa[x]][y][0],f[y==fa[x]][y][1]+z),
		min(val[0][x][i-1].second,max(f[y==fa[x]][y][0],f[y==fa[x]][y][1]+z)-(f[y==fa[x]][y][0]+z)));
	}
	for(int i=tot;i;i--){
		int y=vec[x][i].first,z=vec[x][i].second;
		val[1][x][i]=make_pair(val[1][x][i+1].first+max(f[y==fa[x]][y][0],f[y==fa[x]][y][1]+z),
		min(val[1][x][i+1].second,max(f[y==fa[x]][y][0],f[y==fa[x]][y][1]+z)-(f[y==fa[x]][y][0]+z)));
	}
}
void upd(int x,int i){
	if(!i){
		f[1][x][0]=val[1][x][i+1].first;
		f[1][x][1]=f[1][x][0]-val[1][x][i+1].second;
	}
	else {
		f[1][x][0]=val[0][x][i-1].first+val[1][x][i+1].first;
		f[1][x][1]=f[1][x][0]-min(val[0][x][i-1].second,val[1][x][i+1].second);
	}
}
void dfs2(int x,int p,int pe,int po){
	if(p)upd(p,po);
	calc(x);
	ans=max(ans,f[0][x][0]+max(f[1][p][0],f[1][p][1]+pe));
	int tot=vec[x].size()-2;
	for(int i=1;i<=tot;i++){
		int y=vec[x][i].first,z=vec[x][i].second;
		if(y^p)dfs2(y,x,z,i);
	}
}
int main(){
	scanf("%d",&n);
	for(int i=1,u,v,w;i<n;i++){
		scanf("%d%d%d",&u,&v,&w);
		G[u].push_back(make_pair(v,w));
		G[v].push_back(make_pair(u,w));
	}
	dfs1(1,0,0);
	dfs2(1,0,0,0);
	cout<<ans;
}

总结

换根 DP 的基本思路是两次 dfs，第一次求任一根的所有值，第二次求所有根的根的值。

换根 DP 最需要考虑的问题是如何在第二次 dfs 中转移，即求出一个点被吊起的答案。为了降低复杂度，常常采用预处理前后缀答案的方式来求与一个点相连的所有点中去除一个点后某种满足结合律的运算的答案。