NOIP2021 解题报告

A. 报数

容易想到离线用类似筛法的方式将所有不能报的数标记了，那么我们会得到一个 01 数组 \(v\)。考虑每次询问复杂度得有上限，因此对 \(v\) 求前缀和，每次询问二分到第一个 \(v_j-v_x\ne j-x\) 的 \(j>x\) 即为所求。
分析筛法复杂度。我们可以在如下的代码的基础上，在 check(i) 前面加上 if(!v[i]&&)，避免不必要的枚举。

bool check(int x){
	for(;x;x/=10)if(x%10==7)return 1;
	return 0;
}
for(int i=1;i<=N;i++)
	if(check(i)){
		v[i]=1;
		for(int j=2;j*i<=N;j++)v[i*j]=1;
	}

值得注意的是，\(n=10^7\) 的答案为 \(10^7+1\)，因此前缀和的时候要到 \(10^7+1\) 才是合理的。
代码如下。

#include <bits/stdc++.h>
//#define int long long
//typedef long long ll;
using namespace std;
inline int read(){
	register int x=0,f=1;register char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
	return x*f;
}
const int N=1e7;
int T,n,m,a[N+5],v[N+5];
bool check(int x){
	for(;x;x/=10)if(x%10==7)return 1;
	return 0;
}
signed main(){
//	freopen("number4.in","r",stdin);
//	freopen("number.in","r",stdin);
//	freopen("number.out","w",stdout);
	for(int i=1;i<=N;i++){
		if(!v[i]&&check(i)){
			v[i]=1;
			for(int j=2;j*i<=N;j++)v[i*j]=1;
		}
	}
	for(int i=1;i<=N+1;i++)v[i]+=v[i-1];
	T=read();
	while(T--){
		n=read();
		if(v[n]-v[n-1])puts("-1");
		else{
			int L=n,R=1e7+5,mid;
			while(L<R-1){
			    mid=L+R>>1;
			    if(v[mid]-v[n]<mid-n)R=mid;
			    else L=mid;
			}
			cout<<R<<'\n';
		}
	}
	return 0;
}

B. 数列

本题考查计数 DP。实际上有一定的 DP 能力是一个无需优化、容易推到的 DP，但我的 DP 能力太弱了，今后要加强训练。
当我们审视 \(S\) 的时候，我们会发现它其实就是下面这个东西进位相加的结果。

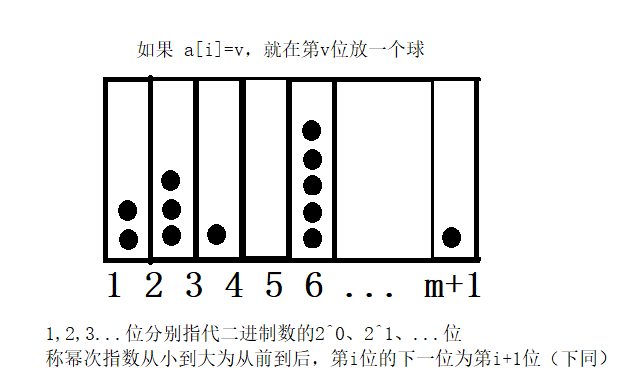
我们发现进位是本题的核心，那这个东西怎样在 DP 状态中体现呢？
我们可以以从一位进到下一位为一步，而连续进位是一小步一小步合起来的，这样一来有了子问题的特征，就可以 DP 了。
设 \(f_{i,j,x,y}\) 表示二进制数的前 \(i\) 位放了 \(j\) 个数，该位进到下一位了 \(x\) 位，前 \(i\) 位还剩 \(y\) 个 \(1\)。
作一注解，就像刚才我们说的“一步”，这个地方的“该位进到下一位”只是进位了“一步”，也就是如果我们现在有 \(11\) 个 \(1\) 在这一位上，那么理论上是要先向下一位进 \(5\)，下一位再向下下位进 \(2\)，等等等等，但是现在我们就让这个进的 \(5\) 先保留在下一位，让下一位进位的时候又进一小步位的时候带着这个 \(5\) 往前进，不知道我说清楚了没有。
那么考虑 \(f_{i,j,x,y}\) 的转移。枚举我们第 \(i\) 位上有多少个球，即 \(\{a\}\) 里头选多少个 \(i\)。
那么当实际的 \(S\) 的第 \(i\) 位是 \(1\) 时：（这个时候相当于是球的个数（包括从下面的位进上来的球）是奇数）
\(f_{i,j,x,y}+=f_{i-1,j-k,2x+1-k,y-1}\times v_i^k/k!\)（注：这里的 \(v_i\) 是题目中的 \(v_{i-1}\)，只是由于我们的下标是从 \(1\) 开始的）
当是 \(0\) 时：
\(f_{i,j,x,y}+=f_{i-1,j-k,2x-k,y}\times v_i^k/k!\)
好，那么为什么这个地方需要除以 \(k!\) 呢？你看上面 \(f_{i,j,x,y}\) 的定义是不是没有宾语。那么考虑由于实质上权值的大小和 \(\{a\}\) 的排列是无关的，所以我们专注于求数组 \(\{a\}\) 是递增的时候的答案，最后再乘上一个东西。考虑你已经求出最后某一个数组 \(\{a\}\) 是递增的时候的状态的答案 \(u\)，真实的答案应该是 \(u\cdot n!\prod\frac{1}{t_i!}\)，其中 \(t_i\) 表示数值 \(i\) 被选了多少个。这个就是一个基本的组合数计算+去重公式。
那么我们在完全地求出了最后的递增的时候的方案再去去重是不可能的，考虑在过程中就把 \(\frac{1}{t_i!}\) 除掉。那么这就是为什么现在要除以 \(k!\)，而最后我们统计答案的时候就是统计所有符合条件的 \(f\) 乘以一个 \(n!\)。
边界条件：\(f_{0,0,0,0}=1\)。
代码实现如下。

#include <bits/stdc++.h>
using namespace std;
const int mod=998244353;
int n,m,p,inv[35],v[105],f[105][35][35][35];
int qp(int a,int b){
	int c=1;
	for(;b;b>>=1,a=1ll*a*a%mod)if(b&1)c=1ll*c*a%mod;
	return c;
}
int main(){
	cin>>n>>m>>p;
	for(int i=1;i<=m+1;i++)cin>>v[i];
	int jc=1,ans=0;inv[0]=1;
	for(int i=1;i<=n;i++)jc=1ll*jc*i%mod,inv[i]=qp(jc,mod-2);
	f[0][0][0][0]=1;
	for(int i=1;i<=m+1;i++)
		for(int k=0;k<=n;k++)
			for(int j=k;j<=n;j++)
				for(int x=0;x<=n;x++)
					for(int y=0;y<=n;y++){
						if(y-1>=0&&2*x+1-k>=0&&2*x+1-k<=n)f[i][j][x][y]+=1ll*f[i-1][j-k][2*x+1-k][y-1]*qp(v[i],k)%mod*inv[k]%mod,f[i][j][x][y]%=mod;
						if(2*x-k>=0&&2*x-k<=n)f[i][j][x][y]+=1ll*f[i-1][j-k][2*x-k][y]*qp(v[i],k)%mod*inv[k]%mod,f[i][j][x][y]%=mod;
					}
	for(int x=0;x<=n;x++)
		for(int y=0;y<=n;y++)
			if(y+__builtin_popcount(x)<=p)
				ans=(ans+f[m+1][n][x][y])%mod;
	cout<<1ll*jc*ans%mod;
}