ABC223-EFG Editorial

ABC223(A~H)
打的是 virtual participation，基本上是第一次打 at，因此前面几题没什么经验虽然无比简单但是做得不够快，另外主要是卡在了 E 题上，100min 的时间实在紧！以下 EFG，F 题是赛后快速做出来的，而 E 题和 G 题是直接看题解的。以下为本场比赛有价值的题目整理(H题看难度就是尚且驾驭不了的)：

E

问是否可能在左下顶点 \((0,0)\)，右上顶点 \((X,Y)\) 的矩形中放置两两没有重合面积的矩形 \(\text{A,B,C}\)，使得 \(S(\text{A})\ge A,S(\text{B})\ge B,S(\text{C})\ge C\)。

先考虑 2 个矩形的情况。通过思考不难发现，一定存在一条平行于 \(x\) 轴/ \(y\) 轴的直线 \(l\) 将大矩形分成两个部分，使得两个矩形分别完整地存在于两个部分中。

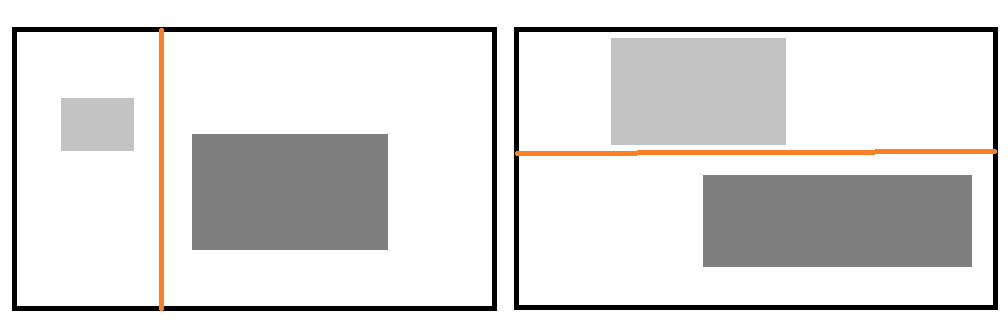
进一步考虑 3 个矩形的情况。类似地，一定可以使大矩形划分成下列 4 种类型中的一种，使得每个矩形完整且独立地分布在其中之一。

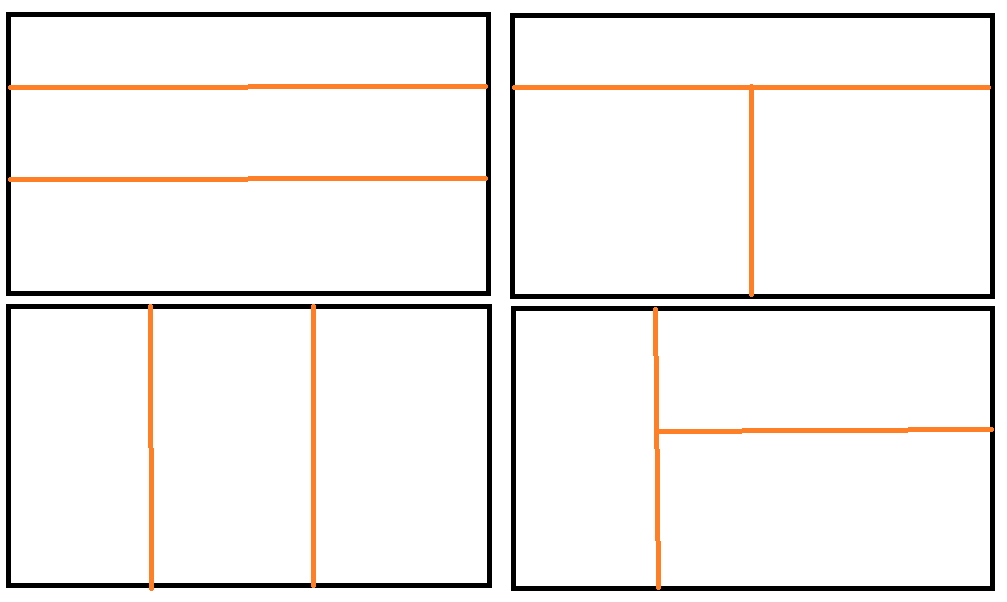
针对每种情况 check 以下是否可行即可。注意 A,B,C 也需要考虑排列（具体见代码）。
https://atcoder.jp/contests/abc223/submissions/27327597

F

给你初始的括号序列 \(S\)，并进行 \(q\) 次询问

• 1 l r：交换 \(S_l,S_r\)
• 2 l r：输出 \(S_{l...r}\) 是不是合法括号序列

引用某博客一句话：遇到这类（关于括号序列和修改查询的）问题，有套路：将 ( 看成 1,) 看成 -1，用数据结构维护。
那么有了套路这题就可以轻松 AC 了。
由于 \(S_{l...r}\) 是合法括号序列的充要条件为 \(\begin{equation} \left\{ \begin{aligned} \forall l\le x\le r,\sum_{i=l}^x a_i\ge 0\\ \sum_{i=l}^ra_i=0\\ \end{aligned} \right. \end{equation}\)，相当于要维护{这个序列的前缀和}的区间最小值和单点查询，考虑使用线段树，并且为了简化代码将单点查询视作对一个长度为 1 的区间的最小值查询。那么修改操作也很容易了，见代码，区间加值即可。
https://atcoder.jp/contests/abc223/submissions/27326777

G

已知树 \(T\)，问有多少个节点 \(u\) 使得从 \(T\) 中删去 \(u\) 和所有与 \(u\) 直接相连的边后，图的最大匹配与 \(T\) 的最大匹配大小相等。

什么是图的最大匹配？

设图的一个边集 \(E'\)，\(E'\) 中的所有边两两没有公共端点，\(|E'|_\max\) 即为最大匹配的大小。

根据官方题解，树的最大匹配的大小即为用下述方法染色后黑点的个数。

• 初始时所有节点为白
• 自下而上地考虑 \(T\)，对于每一个节点如果它的儿子中存在一个白色节点它就染成黑色，否则染成白色

于是，如果根节点为白色，则删去它不会影响，就是一个符合要求的 \(u\)。

利用树形 DP 跑一轮 \(O(n)\) 对树染色，再 dfs 一轮换根 DP 求出每个点作为根时是什么颜色，题目解决。

考虑如何换根 DP。
设第一轮的染色后每个节点的颜色为 \(f_i\)（下面成为“原来的颜色”），同时也用更新 \(f_i\) 的方式求出节点 \(i\) 换作根的颜色。换根之后，\(i\) 的儿子不变色，\(i\) 的父亲 \(p\) 成为 \(i\) 的儿子，那么需要求出 \(p\) 在 \(i\) 作为根时的颜色，从而求出 \(i\) 的颜色。考虑怎么求出 \(p\) 的颜色。相当于节点 \(p\) 此时是被边 \((p,i)\) “吊”起来的，注意到 \(p\) 的除 \(i\) 以外儿子不变色而需要得到 \(p\) 的父节点吊起来的颜色，那么我们可以每次求出一个点吊起来的颜色并递归地传给儿子。不好说。这一部分的实现看代码注释。

#include <bits/stdc++.h>
using namespace std;
const int N=2e5+5;
int n,ans,f[N],fa[N];
vector<int>G[N];
void dfs(int x,int p){ // 第一轮 DP 对树染色
	fa[x]=p;
	for(int i=0;i<G[x].size();i++){
		int y=G[x][i];
		if(y^p){
			dfs(y,x);
			f[x]|=!f[y]; //儿子一旦是白，x就染黑
		}
	}
}
void dfs2(int x,int p,int val){ // val为父节点p被边(x,p)吊起来的颜色
	if(x!=1)f[x]|=!val; // 父节点此时也成了x的儿子，用来更新x作为根的颜色
	vector<int>pv,pp;pv.clear(),pp.clear();pv.push_back(0),pp.push_back(0); 
	// 根据第一轮DP需要求出儿子按位或和的经验，
	// 记录x的儿子的前缀按位或和pv[son]和后缀按位或和pp[son]，
	// 则去除(x,son)后的儿子异或和为pv[son-1]|pv[son+1]
	int siz=G[x].size(),las=0,rl=0;
	for(int i=0;i<siz;i++)if(G[x][i]^p)pv.push_back(las|=!f[G[x][i]]),rl++;
	las=0;
	for(int i=siz-1;i>=0;i--)if(G[x][i]^p)pp.push_back(las|=!f[G[x][i]]);
	pv.push_back(0),pp.push_back(0);
	int lr=0;
	for(int i=1;i<=siz;i++){
		int y=G[x][i-1];
		if(y^p)lr++,dfs2(y,x,(!val)|pv[lr-1]|pp[rl-lr]);
	}
}
int main(){
	cin>>n;
	for(int i=1,u,v;i<n;i++){
		cin>>u>>v;
		G[u].push_back(v);
		G[v].push_back(u);
	}
	dfs(1,0),dfs2(1,0,1);
	for(int i=1;i<=n;i++)ans+=!f[i];
	cout<<ans;
}