割点割边强连通分量

	stk	instk	low[-]==dfn[-]的位置
割点	无需 stk	——	if(low[y]==dfn[x])(循环),if(x==rt)(最后)
割边（通过求E-DCC实现）	需stk	——	if(low[x]==dfn[x])(最后)
SCC	需stk	\(\text{if(instk[y])}\)	if(low[x]==dfn[x])(最后)
V-DCC	需stk	——	if(low[y]==dfn[x])(循环)
E-DCC	需stk	——	if(low[x]==dfn[x])(最后)

Tarjan 是个著名的计算机科学家，他发明了很多算法，在求解图的连通性有关问题时，最著名的应该是割点割边和强连通分量。

什么是割点和割边

在图中去掉这个点和它的所有直接连边，原来联通的图就不联通了，那它就是割点。

在图中去掉这条边，原来联通的图就不联通了，那它就是割边。

非连通图的所有连通块的割点（割边）集合的并是它的割点（割边）集合。

怎么找割点割边

tarjan 算法核心在于 dfs，将图转化为 dfs 树，并记录 dfn（一种dfs序，又名时间戳）。

考虑对图 dfs，dfn[i] 代表 i 节点的访问次序。一次 dfs 下来，由于我们有 if(vis[y])continue; 的判断，所以必然有一些边我们没有走，那那些我们走过的边就必然构成一棵 dfs 树，那些舍弃的边就是 dfs 树中的反向边。

首先，考虑树根。只要树根有多于1个儿子，它就是割点

令 low[i] 表示节点 i 的子树中的节点通过各自的反向边（只走反向边）能够向上回溯到的dfn最小的节点。

想想，\(low[y]\ge dfn[x]\) （y是x的儿子之一）是什么意思？就说明y子树中的节点没有跟x子树外部节点的有效连边。因此，x 就是一个割点。

割边也很好找，因为反向边必然不是割边，因此只要 dfn[y]>x 那边\(x\leftrightarrow y\) 就是割边。且，这时不用特判树根

代码演示（割点）

#include <bits/stdc++.h>
using namespace std;
const int N=2e4+5;
int n,m,tot,cv,dfn[N],low[N];
vector<int>G[N],v;
void tarjan(int x,int p){
	dfn[x]=low[x]=++tot;
	int son=0;bool is=0;
	for(int i=0;i<G[x].size();i++){
		int y=G[x][i];
		if(y==p)continue;
		if(!dfn[y]){
			tarjan(y,x),son++;
			if(low[y]>=dfn[x])is=1;
			low[x]=min(low[x],low[y]);
		}
		else low[x]=min(low[x],dfn[y]); //特别注意，是dfn[y]而不是low[y]
	}
	if(!p&&son>1)cv++,v.push_back(x);
	if(p&&is)cv++,v.push_back(x);
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1,u,v;i<=m;i++)scanf("%d%d",&u,&v),G[u].push_back(v),G[v].push_back(u);
	for(int i=1;i<=n;i++)if(!dfn[i])tarjan(i,0);
	cout<<cv<<'\n';sort(v.begin(),v.end());
	for(int i=0;i<cv;i++)cout<<v[i]<<' ';
}

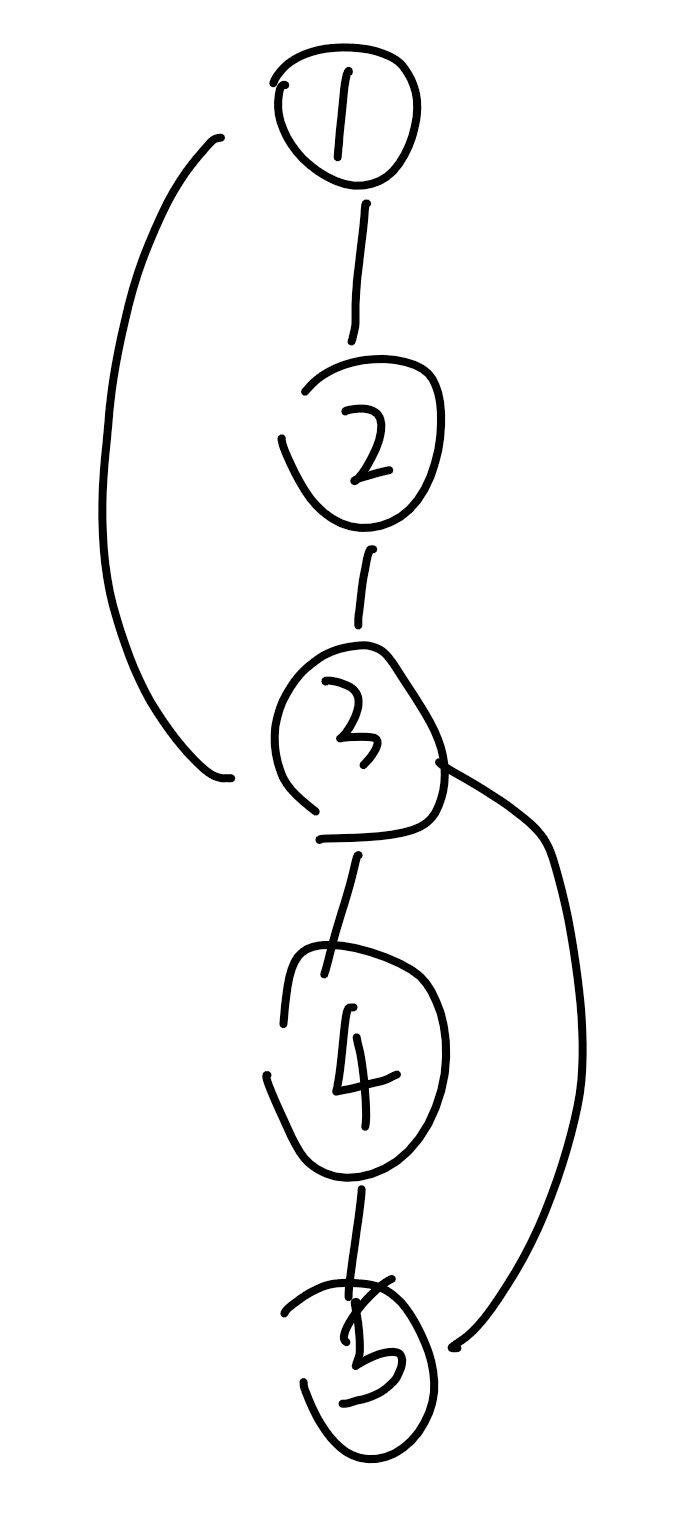
补充：为什么“特别注意”只能是dfn[y]呢？
@Electro_Master 2021-11-07 19:27
反例考虑这样一个图：

代码演示（割边）：比较另类

#include <bits/stdc++.h>
using namespace std;
const int N=60005;
int m1,m2,n,dfc,tp,Cnt,dfn[N],low[N],in[N],p[N],bel[N],stk[N];
vector<pair<int,int> >G[N];
unordered_map<string,int>trans;
pair<int,int>e[N];
bool bk[N],instk[N];
void dfs(int x,int p){
	dfn[x]=low[x]=++dfc,stk[++tp]=x,instk[x]=1;
	for(auto e:G[x]){
		int y=e.first;
		if(!dfn[y]){
			dfs(y,x);
			low[x]=min(low[x],low[y]);
		}
		else if(instk[y])low[x]=min(low[x],dfn[y]);
	}
	if(low[x]==dfn[x]){
		Cnt++;
		while(tp){
			bel[stk[tp]]=Cnt;
			instk[stk[tp]]=0;
			if(stk[tp--]==x)break;
		}
	}
}
//main
for(int i=1;i<=m1;i++)cout<<(bel[e[i].first]!=bel[e[i].second]?"Safe":"Unsafe")<<'\n';//是否是割边

什么是（有向图的）强连通分量

有向图的一个极大联通子图是它的一个强连通分量。

两个要点：极大，联通。联通好理解，分量中任意两点\(u\to v\) 两两可达。注意！有向图，因此仅仅u可达v,v却不可达u是不可以的；极大：如果一个强连通分量的子连通分量也是一个节点两两可达的子图，那它也不算一个强连通分量，因为还有比他更大且包含它的

怎么找强连通分量

代码其实和割点割边差不太多，做法含义有所不同

同样有low,dfn两个数组，还有一个栈。到达一个点就把它入栈，查看它的所有儿子，如果不是反向边，就递归这个儿子，然后更新low[x]=min(low[x],low[y])。如果是反向边，注意，如果反向边的那一头是一个已经找到强连通分量的点，那就忽略这条边，否则，更新low[x]。一个要点是，只有还没有找到强连通分量的点才在栈中，段末有解答。

当我们查看完所有x的儿子后，我们判断x是不是强连通分量的根。他是一个强联通分量的根当且仅当此时还low[x]=dfn[x]，那么这个强连通分量包含的节点就是x的子树中所有还没找到归属地的节点，这些节点哪里找，就在栈顶到栈中x所在位置的这一个区间，我们把他们收拾起来，然后一一退栈（已经不需要解答了吧）

代码(模板题链接)

#include <bits/stdc++.h>
using namespace std;
const int N=1e4+5;
int top,ord,Bcnt;
int stk[N],instk[N],dfn[N],low[N];
vector<int>G[N],B[N];
void scc(int x){
	dfn[x]=low[x]=++ord;
	stk[++top]=x,instk[x]=1;
	for(int i=0;i<G[x].size();i++){
		int y=G[x][i];
		if(!dfn[y]){
			scc(y);
			low[x]=min(low[x],low[y]);
		}
		else if(instk[y])low[x]=min(low[x],low[y]);
	}
	if(dfn[x]==low[x]){
		Bcnt++;
		while(top){
			instk[stk[top]]=0;
			B[x].push_back(stk[top]);
			if(stk[top--]==x)break;
		}
		sort(B[x].begin(),B[x].end());
		if(x!=B[x].front())B[B[x].front()]=B[x],B[x].clear();
	}
}
int main()
{
	int n,m,u,v;
	cin>>n>>m;
	for(int i=1;i<=m;i++)cin>>u>>v,G[u].push_back(v);
	for(int i=1;i<=n;i++)if(!dfn[i])scc(i);
	cout<<Bcnt<<endl;
	for(int i=1;i<=n;i++){
		if(!B[i].size())continue;
		for(int j=0;j<B[i].size();j++)cout<<B[i][j]<<' ';puts("");
	}
}

缩点

缩点就是强联通分量的应用。对于每一个强联通分量缩成一个新的点，构成一张新的缩点后的图。
模板题链接：luoguP3387

#include <bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n,m,a[N],dfn[N],low[N],instk[N],stk[N],b[N],t,tot,Bcnt,bel[N],in[N],f[N];
vector<int>G[N],nG[N],B[N];
queue<int>Q;
void scc(int x){
	dfn[x]=low[x]=++tot,instk[x]=1,stk[++t]=x;
	for(int i=0;i<G[x].size();i++){
		int y=G[x][i];
		if(!dfn[y]){
			scc(y);
			low[x]=min(low[x],low[y]);
		}else if(instk[y])low[x]=min(low[x],low[y]);
	}
	if(dfn[x]==low[x]){
		Bcnt++;
		while(t){
			instk[stk[t]]=0;
			B[Bcnt].push_back(stk[t]);
			bel[stk[t]]=Bcnt;
			b[Bcnt]+=a[stk[t]]; 
			if(stk[t--]==x)break;
		}
	}
}
int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)cin>>a[i];
	for(int i=1,u,v;i<=m;i++){
		cin>>u>>v;
		G[u].push_back(v);
	}
	for(int i=1;i<=n;i++)if(!dfn[i])scc(i);
	for(int x=1;x<=Bcnt;x++)
		for(int i=0;i<B[x].size();i++){
			int xx=B[x][i];
			for(int j=0;j<G[xx].size();j++){
				int yy=G[xx][j];
				if(bel[xx]!=bel[yy])nG[bel[xx]].push_back(bel[yy]),in[bel[yy]]++;
			}
		}//for(int i=1;i<=n;i++)printf("%d ",bel[i]);puts("");
	for(int i=1;i<=Bcnt;i++)if(!in[i])Q.push(i),f[i]=b[i];
	while(!Q.empty()){
		int x=Q.front();Q.pop();
		for(int i=0;i<nG[x].size();i++){
			int y=nG[x][i];
			in[y]--,f[y]=max(f[y],f[x]+b[y]);
			if(!in[y])Q.push(y);
		}
	}
	int ans=0;
	for(int i=1;i<=Bcnt;i++)ans=max(ans,f[i]);
	cout<<ans<<endl;
}