平衡树2
重学 Splay
时隔一年半,我又捡起了 Splay,并决定再也不要忘记它。记录一些要点,辅助理解。
Splay 实现的函数及他们之间的关系见下:
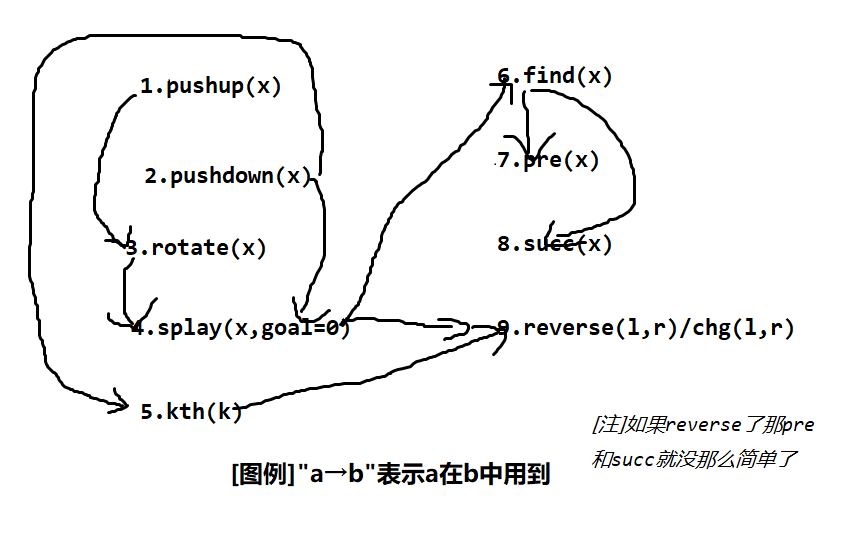
含义:
pushup(x):更新 \(x\) 的 \(siz,dat\)。\(dat\) 维护子树代表的区间内的答案。pushdown(x):把 \(x\) 的 tag 下传。rotate(x):单旋转。splay(x,goal=0):把 \(x\) 双旋转直到成为 \(goal\) 的儿子,\(goal=0\) 时表示旋转到根,此时需要注意更新 \(root\)。双旋转:\(y,z\) 分别为 \(x\) 的父亲和爷爷,当 \(x,y,z\) 三点共线时,rotate(y),rotate(x),否则 \(rotate(x),rotate(x)\)。通常需要pushdown。kth(k):找到中序遍历第 \(k\) 个节点。注意 \(val\) 不直接影响它。find(x):找到 \(val\le x\) 且 \(val\) 最大节点,并splay到根。pre(x)/succ(x):找到数值 \(x\) 的前驱与后继节点。reverse(l,r)/chg(l,r)/ask(l,r):对区间 \([l,r]\) 的翻转、修改、查询操作,需要先把 \(l-1\)splay到根,\(r+1\)splay到根的右儿子(这两部合称 split),根的右儿子的左儿子对应的子树即表示 \([l,r]\)。
【例】T4后缀数组
只此一道,就能让你完全 Splay 维护区间操作的基本构架。
e.g. reverse[l,r]
一,split 出 [l,r],记子树根为 k
二,把 k 打上 rev 标记,并更新节点k自身的信息以及k所代表的子树的信息,相当于线段树的if(L<=l&&r<=R){}中的内容。
三,在kth(),splay()和lower_bound()等函数中加上pushdown()
四,在pushup函数中加上维护相关信息的语句
Module
inline void pushup(int k){
{stuff...}
t[k].siz=t[t[k].ch[0]].siz+t[t[k].ch[1]].siz+1;
}
inline void pushdown(int k){
if(t[k].rev){
if(t[k].ch[0])t[t[k].ch[0]].rev^=1,{stuff...}
if(t[k].ch[1])t[t[k].ch[1]].rev^=1,{stuff...}
t[k].rev=0;
}
if(t[k].fl){
if(t[k].ch[0])t[t[k].ch[0]].fl^=1,{stuff...}
if(t[k].ch[1])t[t[k].ch[1]].fl^=1,{stuff...}
t[k].fl=0;
}
}
inline void rotate(int x){
int y=t[x].fa,z=t[y].fa,k=chk(x);
t[y].ch[k]=t[x].ch[k^1],t[t[x].ch[k^1]].fa=y;
t[z].ch[chk(y)]=x,t[x].fa=z;
t[x].ch[k^1]=y,t[y].fa=x;
pushup(y),pushup(x);
}
inline void splay(int x,int goal=0){
while(t[x].fa!=goal){
int y=t[x].fa,z=t[y].fa;
if(z!=goal){
if(chk(x)==chk(y))rotate(y);
else rotate(x);
}
rotate(x);
}
if(!goal)root=x;
}
inline int kth(int x){
if(x<1||x>n+2)return 0;
int k=root;
while(1){
pushdown(k);
if(t[t[k].ch[0]].siz>=x)k=t[k].ch[0];
else if(t[t[k].ch[0]].siz+1>=x)return k;
else x-=t[t[k].ch[0]].siz+1,k=t[k].ch[1];
}
return k;
}
inline int split(int l,int r){
int x=kth(l),y=kth(r+2);
if(!x||!y)return 0;
splay(x),splay(y,x);
return t[y].ch[0];
}
inline void reverse(int l,int r){
int k=split(l,r);
t[k].rev^=1;
{stuff...}
pushup(t[k].fa),pushup(t[t[k].fa].fa);
}
inline void flip(int l,int r){
int k=split(l,r);
t[k].fl^=1;
{stuff...}
pushup(t[k].fa),pushup(t[t[k].fa].fa);
}
inline void insert(int x){
int cur=root,p=0;
while(cur&&t[cur].val!=x){
pushdown(cur);
p=cur;
cur=t[cur].ch[x>t[cur].val];
}
t[++tot].val=x,t[tot].siz=1;
if(p)t[tot].fa=p,t[p].ch[x>t[p].val]=tot;
{other things...}
splay(tot);
}
简介
Splay 也是一种平衡树,中文叫做伸展树。它的独特操作不再是用随机性来保持平衡,而是认为“最近一次操作的是什么,我们就认为下次出现概率最大的是什么操作,因此要把操作过的这个节点搬到根节点去”。这一种操作就是 \(splay(p,to)\) 代表把节点 \(p\) 旋转到 \(to\) 的子节点里。每个操作完,将操作后的节点 splay 到根(-INF)节点的子树。
与 Treap 不同的是,我们发现 splay 的旋转操作是朝上去的而不是朝下到叶子,因此我们旋转的主语变成原来处在孩子位置的节点,并且不再分 zigzag。称它 rotate(p) 表示将节点 p 上旋。
struct Node {
int fa,son[2];
int val,cnt,size;
}a[N]; int root,tot;
int New(int val){
a[++tot].val=val;
a[tot].cnt=a[tot].size=1;
return tot;
}
void Update(int p){
a[p].size=a[a[p].son[0]].size+a[a[p].son[1]].size+a[p].cnt;
}
int identify(int p) { return a[a[p].fa].son[1]==p; }
void connect(int fa,int id,int p) { a[fa].son[id]=p,a[p].fa=fa; }
void Build(){
New(-INF),New(INF);
root=1,connect(1,1,2);
Update(root);
}
void Rotate(int p){
int q=a[p].fa,r=a[q].fa;
int ip=identify(p),iq=identify(q);
a[q].son[ip]=a[p].son[ip^1];
connect(q,ip,a[p].son[ip^1]);
connect(p,ip^1,q);
connect(r,iq,p);
Update(q),Update(p);
}
splay 函数用到一个叫双旋转的东西:事实证明将一个节点向上旋转不能只每次单选上去,要分类讨论:如果该节点,该节点的父节点,该节点父节点的父节点,三点共线,那么,先旋父节点,再旋该节点;不共线,那么旋两次该节点即可。
void splay(int p,int to){
if(a[p].fa==to) return;
while(a[p].fa!=to){
int fa=a[p].fa;
if(a[fa].fa==to) Rotate(p);
else if(identify(p)==identify(fa)) Rotate(fa),Rotate(p);
else Rotate(p),Rotate(p);
}
}
其他的没什么不同。
还是【普通平衡树】,代码:
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+5,INF=1e9;
struct Splay {
int fa,son[2];
int val,cnt,size;
}a[N]; int root,tot;
int New(int val){
a[++tot].val=val;
a[tot].cnt=a[tot].size=1;
return tot;
}
void Update(int p){
a[p].size=a[a[p].son[0]].size+a[a[p].son[1]].size+a[p].cnt;
}
int identify(int p) { return a[a[p].fa].son[1]==p; }
void connect(int fa,int id,int p) { a[fa].son[id]=p,a[p].fa=fa; }
void Build(){
New(-INF),New(INF);
root=1,connect(1,1,2);
Update(root);
}
void Rotate(int p){
int q=a[p].fa,r=a[q].fa;
int ip=identify(p),iq=identify(q);
a[q].son[ip]=a[p].son[ip^1];
connect(q,ip,a[p].son[ip^1]);
connect(p,ip^1,q);
connect(r,iq,p);
Update(q),Update(p);
}
void Balance(int p,int to){//即splay
if(a[p].fa==to) return;
while(a[p].fa!=to){
int fa=a[p].fa;
if(a[fa].fa==to) Rotate(p);
else if(identify(p)==identify(fa)) Rotate(fa),Rotate(p);
else Rotate(p),Rotate(p);
}
}
int Get(int p,int val){
if(p==0) return 0;
if(val==a[p].val){
Balance(p,root);
return p;
}
return val<a[p].val?Get(a[p].son[0],val):Get(a[p].son[1],val);
}
int Insert_init(int p,int val){
if(val==a[p].val){
a[p].cnt++;
return p;
}
int next=val<a[p].val?0:1;
if(!a[p].son[next]){
a[p].son[next]=New(val);
connect(p,next,a[p].son[next]);
return a[p].son[next];
}
return val<a[p].val?Insert_init(a[p].son[0],val):Insert_init(a[p].son[1],val);
}
void Insert(int p,int val){
int d=Insert_init(p,val);
Balance(d,root);
}
void Remove(int val){
int p=Get(root,val);
if(a[p].cnt>1){
a[p].cnt--,Update(p);
return;
}
if(!a[p].son[0]){
connect(root,1,a[p].son[1]);
return;
}
int l=a[p].son[0];
while(a[l].son[1]>0) l=a[l].son[1];
Balance(l,p);
connect(l,1,a[p].son[1]);
connect(root,1,l);
Update(l);
}
int GetPre(int val){
int p=root;
int ans=1;
while(p){
if(val==a[p].val){
if(a[p].son[0]>0){
p=a[p].son[0];
while(a[p].son[1]>0) p=a[p].son[1];
ans=p;
}
break;
}
if(a[p].val<val && a[p].val>a[ans].val) ans=p;
p=val<a[p].val?a[p].son[0]:a[p].son[1];
}
return a[ans].val;
}
int GetNext(int val){
int p=root;
int ans=2;
while(p){
if(val==a[p].val){
if(a[p].son[1]>0){
p=a[p].son[1];
while(a[p].son[0]>0) p=a[p].son[0];
ans=p;
}
break;
}
if(a[p].val>val && a[p].val<a[ans].val) ans=p;
p=val<a[p].val?a[p].son[0]:a[p].son[1];
}
return a[ans].val;
}
inline int GetRankByVal(int p,int val){
if(p==0) return 0;
if(val==a[p].val){
int res=a[a[p].son[0]].size+1;
Balance(p,root);
return res;
}
if(val<a[p].val) return GetRankByVal(a[p].son[0],val);
else return a[a[p].son[0]].size+a[p].cnt+GetRankByVal(a[p].son[1],val);
}
int GetValByRank(int p,int rank){
if(p==0) return INF;
if(rank<=a[a[p].son[0]].size) return GetValByRank(a[p].son[0],rank);
if(rank<=a[a[p].son[0]].size+a[p].cnt){
Balance(p,root);
return a[p].val;
}
return GetValByRank(a[p].son[1],rank-a[a[p].son[0]].size-a[p].cnt);
}
int main()
{
//freopen("s.in","r",stdin);
//freopen("s.out","w",stdout);
ios::sync_with_stdio(false);
Build();
int m;
cin>>m;
int opt,x;
while(m--){
cin>>opt>>x;
if(opt==1) Insert(root,x);
if(opt==2) Remove(x);
if(opt==3) cout<<GetRankByVal(root,x)-1<<'\n';
if(opt==4) cout<<GetValByRank(root,x+1)<<'\n';
if(opt==5) cout<<GetPre(x)<<'\n';
if(opt==6) cout<<GetNext(x)<<'\n';
}
return 0;
}
【例】超级备忘录
区间操作,我们的作为平衡规则的不再是键值,而是序列编号。
这篇题解讲得很好,不用考虑 \(f_4 f_5\)。
通过这道题目我们可以发现,splay 操作有个很神奇的功能叫 split,他可以在区间问题中将一个区间独立划分到一个子树中。而处理边界问题我们可以预先插入一个序号 0,再插入一个序号 n+1。
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+5,INF=1e9;int s[N];
struct Node {
int fa,son[2];
int size,dat,mindat;
int rev,add;
}a[N]; int root,tot;
int New(int fa,int dat){
a[++tot].fa=fa;
a[tot].dat=a[tot].mindat=dat;
a[tot].size=1;
return tot;
}
int idfy(int p){
return a[a[p].fa].son[1]==p;
}
void connect(int fa,int p,int id){
a[fa].son[id]=p;
a[p].fa=fa;
}
void pushup(int p){
a[p].size=a[a[p].son[0]].size+a[a[p].son[1]].size+1;
a[p].mindat=a[p].dat;
if(a[p].son[0]) a[p].mindat=min(a[p].mindat,a[a[p].son[0]].mindat);
if(a[p].son[1]) a[p].mindat=min(a[p].mindat,a[a[p].son[1]].mindat);
}
void build() {
root=1;
New(0,-INF);
a[1].son[1]=New(1,INF);
pushup(root);
}
void pushdown(int p){
if(a[p].rev){
a[a[p].son[0]].rev^=1,a[a[p].son[1]].rev^=1;
swap(a[p].son[0],a[p].son[1]);
}
if(a[p].add){
a[a[p].son[0]].dat+=a[p].add,a[a[p].son[1]].dat+=a[p].add;
a[a[p].son[0]].add+=a[p].add,a[a[p].son[1]].add+=a[p].add;
a[a[p].son[0]].mindat+=a[p].add,a[a[p].son[1]].mindat+=a[p].add;
}
a[p].rev=a[p].add=0;
}
void rotate(int p){
int q=a[p].fa,r=a[q].fa;
int ip=idfy(p),iq=idfy(q);
connect(q,a[p].son[ip^1],ip);
connect(p,q,ip^1);
connect(r,p,iq);
pushup(q),pushup(p);
}
void splay(int p,int to){
if(p==to) return;
while(a[p].fa!=to){
int fa=a[p].fa;
if(a[fa].fa!=to)
if(idfy(p)==idfy(fa)) rotate(fa);
else rotate(p);
rotate(p);
}
}
int kth(int rank){
int p=root;
while(p){
pushdown(p);
if(rank==a[a[p].son[0]].size+1) return p;
if(rank<=a[a[p].son[0]].size) p=a[p].son[0];
else rank-=a[a[p].son[0]].size+1,p=a[p].son[1];
}
}
int split(int l,int r,int dir){
int c[2]={kth(l+1),kth(r+3)};
splay(c[dir^1],root);
splay(c[dir],c[dir^1]);
return a[a[a[root].son[1]].son[dir]].son[dir^1];
}
void revolve(int l,int r,int t){
int f1=split(l,r-t,0),f2=a[f1].fa;
pushdown(a[f2].fa),pushdown(f2);
a[f2].son[1]=0;
pushup(f2),pushup(a[f2].fa);
int f3=split(r-t+1-a[f1].size,r-a[f1].size,1),f4=a[f3].fa;
pushdown(f3);
while(a[f3].son[1]) f3=a[f3].son[1],pushdown(f3);
splay(f3,f4);
connect(f3,f1,1);
pushup(f3),pushup(f4),pushup(a[f4].fa);
}
int main()
{
int n,m;
string opt;
int l,r,x;
cin>>n;
build();
a[2].son[0]=New(2,0); pushup(2);
for(int i=1;i<=n+1;i++){
if(i<=n) cin>>x;
int p=kth(i+1);
splay(2,root);
splay(p,2);
a[p].son[1]=New(p,x);
pushup(p),pushup(2);
}
cin>>m;
while(m--){
cin>>opt;
if(opt=="ADD"){
cin>>l>>r>>x;
int p=split(l,r,1);
a[p].dat+=x;
a[p].add+=x;
a[p].mindat+=x;
pushup(a[p].fa),pushup(a[a[p].fa].fa);
}
if(opt=="REVERSE"){
cin>>l>>r;
a[split(l,r,1)].rev^=1;
}
if(opt=="REVOLVE"){
cin>>l>>r>>x; x%=r-l+1;
if(x) revolve(l,r,x);
}
if(opt=="INSERT"){
cin>>l>>x;
int p=split(l,l,1),q=a[p].fa,r=a[q].fa;
pushdown(p);
a[p].son[1]=New(p,x);
pushup(p),pushup(q),pushup(r);
}
if(opt=="DELETE"){
cin>>l;
int p=split(l,l,1);
a[a[p].fa].son[0]=0;
pushup(a[p].fa),pushup(a[root].son[1]);
}
if(opt=="MIN"){
cin>>l>>r;
int p=split(l,r,1);
pushdown(p);
cout<<a[p].mindat<<endl;
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号