背包

背包问题是动态规划问题中常见的一个分支，常用的有 01背包，完全背包，和多重背包，本篇文章详解01背包和完全背包。

01背包

问题描述：有一个容量为 \(m\) 的背包，有 \(n\) 个物品每个只有一件，第 \(i\) 个物品占用 \(w_i\) 单位空间、拥有 \(c_i\) 的价值，求问在这个背包中放入若干物品使得不超出容量限制，所能获得的最大价值是多少。

01背包，顾名思义，0表示不选择当前的物品，1表示选择当前的物品。每种物品有选与不选两种情况，如果用 DFS 取所有方案最大值的话复杂度 \(2^n\) 一定超时。用动态规划的方法可以解决。

定义状态：\(f_{i,j}\) 表示在只有 \(1\sim i\) 这 \(i\) 个物品的情况下选择若干装进一个容量为 \(j\) 的背包所能获得的最大价值。我们知道，当 \(i=0\) 时不能获得价值（\(f_{0,(1,2,\ldots,m)}=0\)），当背包没有容量时也不能获得价值（\(f_{(1,2,\ldots,n),0}=0\)），其实在全局变量里面定义 \(f\) 就可以解决了。

对于我们当前的 \(f_{i,j}\)，可能选或不选。如果选第 \(i\) 个物品：那么我们的价值就等于选的这个物品的价值再加上背包中剩下容量装 \(1\sim i-1\) 物品所能获得的最大价值，即 \(f_{i,j}=c_i+f_{i-1,j-w_i}\)；此时，显然背包要得装得下这个物品才行，否则没法选他。如果不选第 \(i\) 个物品：那么我们的价值就等于用现在的背包容量去装 \(1\sim i-1\) 物品所能获得的最大价值，即 \(f_{i,j}=f_{i-1,j}\)。我们在选与不选所得的答案中取一个最大值就是当前背包的最大价值了。我们写出以下代码：

#include <iostream>
using namespace std
const int N=1e3,M=5e4;
int f[N][M],c[N],w[N];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>w[i]>>c[i];
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            if(j>=w[i]) //要的装得下
                f[i][j]=max(f[i-1][j],c[i]+f[i-1][j-w[i]]);
            else //装不下就相当于是f[i-1][j]了
                f[i][j]=f[i-1][j];
    cout<<f[n][m]<<endl;
    return 0;
}

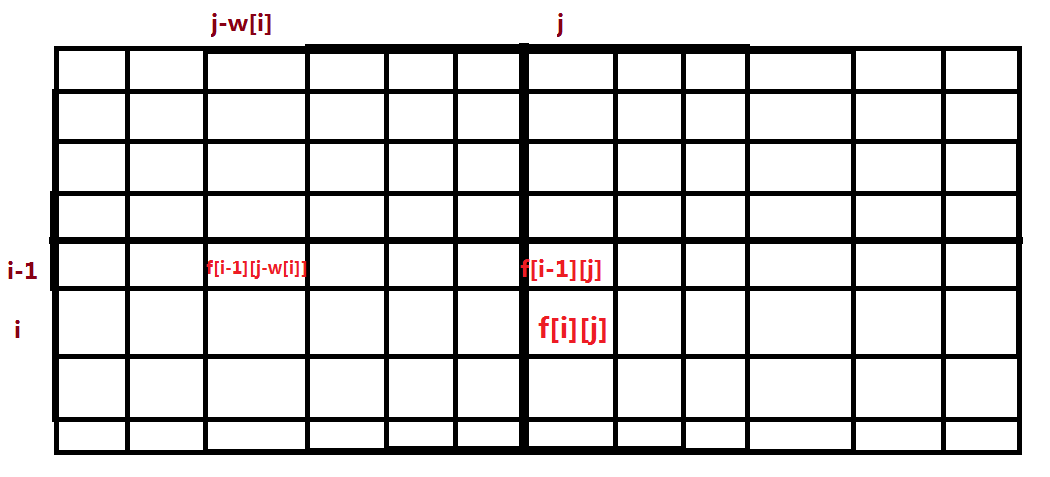
看看这张图片，其中标出了我们要取 \(\max\) 的两个答案，我们发现他们都是在第 \(i-1\) 行也就是刚刚我们操作完的那一行。设想如果我们只用一个一维的数组 \(f\) 储存刚刚处理完的那些结果，那么我们就可以在这个基础上，获取我们需要的信息，从而 \(f_{i,j}=\max(f_{i-1,j},c_i+f_{i-1,j-w_i})\) 转化成了 \(f_j=\max(f_j,c_i+f_{j-w_i})\)。好的，那请你想一想，我们 for(int j=1;j<=m;j++) 这个循环跟 for(int j=m;j>=1;j--) 对答案有影响吗？是有的，因为如果用第一种（正向）那么我们的 \(f_{j-w_i}\) 就已经不再是原来的 \(f_{j-w_i}\) 即之前所说的二维数组中上一排的了，而是我们在二维数组 \(f\) 中这一排的答案了，如果我们反向循环就可以消除这个问题。这就是所谓的“滚动数组”，滚掉了一维。最终的代码：

#include <iostream>
using namespace std
const int N=1e3,M=5e4;
int f[M],c[N],w[N];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>w[i]>>c[i];
    for(int i=1;i<=n;i++)
        for(int j=m;j>=w[i];j++)
                f[j]=max(f[j],c[i]+f[j-w[i]]);
    cout<<f[m]<<endl;
    return 0;
}

完全背包

问题描述：有一个容量为 \(m\) 的背包，有 \(n\) 个物品每个有无数件，第 \(i\) 个物品占用 \(w_i\) 单位空间、拥有 \(c_i\) 的价值，求问在这个背包中放入若干物品使得不超出容量限制，所能获得的最大价值是多少。

我告诉你，下面的代码就是答案。

#include <iostream>
using namespace std
const int N=1e3,M=5e4;
int f[M],c[N],w[N];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>w[i]>>c[i];
    for(int i=1;i<=n;i++)
        for(int j=w[i];j<=m;j++)
                f[j]=max(f[j],c[i]+f[j-w[i]]);
    cout<<f[m]<<endl;
    return 0;
}

显然这就是滚动数组之后的一维 \(f\) 数组的代码，而它与01背包的最终代码唯一的不同，就是我们是按照之前所说的“错误枚举顺序”——正向循环的。为什么这样子在完全背包是正确的呢？敬请看后文。

我们知道，反向枚举就是调用的二维数组上一行的信息，而正向枚举就是调用的二维数组这一行算出来的信息。对于这个背包，我们同样有选与不选两种情况。当然装不下就不用管，装得下：

• 不选的话，答案就不变，跟01背包一样的道理。
• 选的话，也就是说我们至少需要选择一个这种物品，那么我们就选择一个这种物品，剩下的就交给我们这一排算好的 \(f_{j-w_i}\) 就好了。

对于上面两种情况取一个 \(\max\) 得到递推关系式 \(f_j=\max(f_j,c_i+f_{j-w_i})\)，但是这跟01背包的关系式是本质不同的，完全背包的关系式如果在二维数组中应该是：\(f_{i,j}=\max(f_{i-1,j},c_i+f_{i,f-w_i})\)。边界条件与01背包相同：\(f_{0,(1,2,\ldots,m)}=0\)，\(f_{(1,2,\ldots,n),0}=0\)。

其实完全背包还有另外的解法（复杂度不比刚才说的解法优）。其原理是这样的：

我们可以把完全背包问题化成01背包问题，即每个物品其实最多只能选 \(\lfloor \frac{m}{w_i} \rfloor\) 件，所以我们就把每个物品看作是 \(\lfloor \frac{m}{w_i} \rfloor\) 个占用 \(w_i\) 单位空间、拥有 \(c_i\) 价值的物品，最后求解这个01背包问题即可，这个复杂度是很有些高的。

我们想想，是不是真的有必要把他分成这么多数量的同种物品？不要曲解我的意思，我的意思并不是说“只需要一个范围内数量的物品就够了，超出这个数量的物品都用不上”，我的意思是说我，我们可以把一些物品合并到一起，从而减少了总物品数量，优化了复杂度。

看：每一个自然数 \(n\) 都可以化成若干个 \(2\) 的幂次相加的形式；为什么是这样——因为 \(n\) 化成二进制就只由 \(0,1\) 组成，而 \(2\) 的幂次化成二进制就是一个 \(1\) 后面跟若干个 \(0\) 的形式（准确来说，\(2^k\) 的二进制形式是一个 \(1\) 后面 \(k\) 个 \(0\)），所以打比方说，十进制数 \(5\) 的二进制数是 \((101)_2=(100)_2+(1)_2=(4)_{10}+(1)_{10}\)。既然这样，那么我们说这个可以有无限多的物品我们取的次数就也可以化成若干个二进制数相加的形式喽，那我们就只需要配备：体积和价值都是原来的 \(2^k\) 倍的物品了。举个例子就不那么抽象：

我们当前这个物品体积为 \(3\)，价值为 \(5\)，可以取无数个，且 \(m=10\)。那么我们知道他最多只能取 \(\lfloor \frac{10}{3} \rfloor=3\) 个，那如果选他，他可能取 \(1\) 或 \(2\) 或 \(3\) 个，所以我们只需要配备 \(2^0\) 和 \(2^1\) 这两个物品，因为 \(1=2^0\)，\(2=2^1\)，\(3=2^0+2^1\)。所以我们转成01背包时把这个物品拆成的物品就应该有两个：

	体积	价值
第一个	\(2^0\times 3=3\)	\(2^0\times 5=5\)
第二个	\(2^1\times 3=6\)	\(2^1\times 5=10\)

其实这样还是没有最经典的（最开头谈的）那个方法复杂度低，所以就不展示代码了。谢谢大家，希望看了这篇文章你能对背包有更清楚的认识。